摘要:在声速测定实验中, 接收换能器位置对谐振频率测量结果有一定影响。目前, 对这种影响的研究较少。研究接收换能器输出电压随接收换能器位置的变化, 发现当两个换能器间距较小时, 不同频率下的输出电压极大值的位置是聚集的, 随着换能器间距的增加该位置逐渐发散。当换能器间距较小且接收换能器处于干涉极小值位置时, 谐振频率测量不受共振干涉的影响。
关键词:声速测量; 换能器; 谐振频率; 共振干涉;
声速测定实验是大学物理实验中的一个基本实验[1,2], 通常利用共振干涉法和相位比较法测量声波波长λ, 从声速测定仪信号源前面板读出声波频率, 代入声速计算公式V=λf, 进而求得声速[3].由于声波振动幅值随发射换能器 (为了便于描述, 该换能器简称为换能器S1) 和接收换能器 (为了便于描述, 该换能器简称为换能器S2) 的距离 (为了便于描述, 该距离定义为距离L) 增加而快速衰减, 不易在换能器S1和换能器S2之间形成驻波, 另外声波信号的幅值较小也会导致换能器S2的灵敏度降低。因此在测定声速之前, 需要确定系统的谐振频率。
谐振频率确定方法通常为:固定换能器S1和换能器S2之间距离L, 慢慢调节输入信号频率, 当换能器S2的输出电压达到最大时, 对应的信号频率为系统的谐振频率。在实验过程中发现, 换能器S2的位置不同, 谐振频率的测量值存在差别, 即换能器S2的位置对谐振频率测量有影响。为了进一步提高谐振频率的测量精度, 再次改变换能器S2位置, 重复测量五次取平均值[4], 换能器S2位置对谐振频率测量精度的影响机理目前不很清楚。文献[5]虽然报道了换能器S2的位置对谐振频率测量精度的影响, 并提出定量定性解释, 但是测量谐振频率时, 换能器S2究竟处于什么位置时谐振频率测量较为精确还不清楚。为此本文研究了不同输入信号频率下, 换能器S2输出电压随换能器S2位置变化, 确定了精确测量谐振频率时换能器S2位置的方法, 给出相应的物理解释。
1 实验仪器
本文所采用的实验装置示意图如图1所示。
信号源是杭州大华仪器制造有限公司的综合声速测定仪信号源。该信号源能输出20 000赫兹以上的交流信号, 信号幅值和频率连续可调。换能器S1和换能器S2为压电晶体换能器。为避免实验仪器在两个换能器间距L小于10 mm时出现假峰现象[6,7], 在测定谐振频率之前, 检测多台声速测量仪, 选择其中一台没有假峰现象的声速测量仪作为本文使用的声速测量仪。可以通过手摇鼓轮改变换能器S2的位置, 手摇鼓轮的最小精度为0.01 mm.为了精确测量换能器S2的输出电压, 电压信号利用美国泰克公司的DPO4104型四通道的数字存贮示波器测量, 该示波器的技术参数为:输入阻抗是1MΩ/50Ω, 带宽是500 MHz, 最小输入灵敏度 (1MΩ) 是1 m V/div.
2 实验结果
连接好仪器, 使用前开机预热10分钟, 自动工作在连续被方式, 连续波强度和接收增益固定不变, 换能器S1和换能器S2之间的介质为空气, 两换能器保持平行。下面的实验都采用同样的步骤和设置。
2.1 换能器S2位置对输出电压的影响
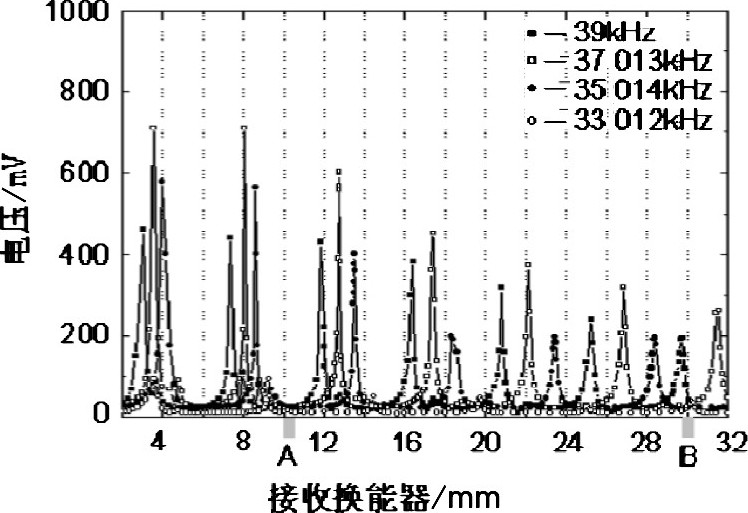
输入信号频率固定为39 k Hz, 通过手摇鼓轮改变换能器S2的位置, 利用示波器测量该位置下换能器S2输出电压, 得到输出电压随换能器S2位置的变化曲线。输入信号频率分别固定为37.013 k Hz, 35.014 k Hz, 33.012 k Hz, 重复上述测量过程, 得到不同频率下输出电压随换能器S2位置变化曲线 (见图2) .
信号频率分别是39 k Hz, 37.013 k Hz, 35.014k Hz, 33.012 k Hz.
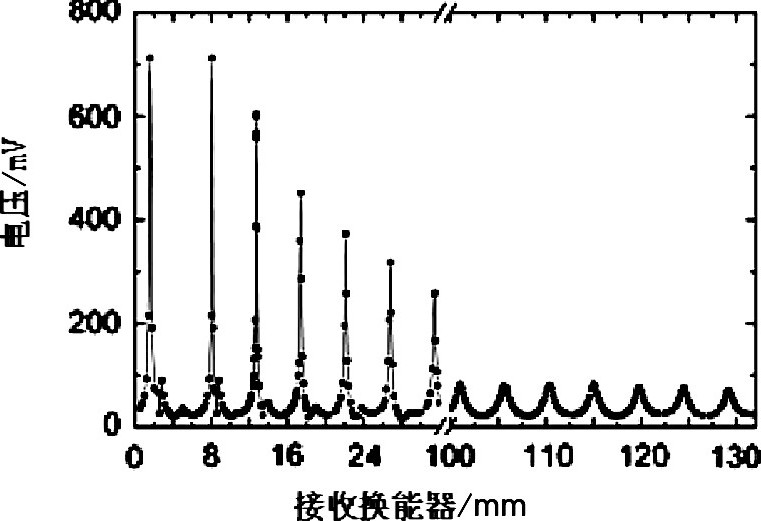
从图2可以看出: (1) 换能器S1和换能器S2间距L较小时, 不同频率的同一干涉级的极大值对应的位置间距差 (为了便于描述, 该极大值对应的位置间距差定义为ΔL) 较小, 也就是说, 间距L较小时, 极大值位置较为集中;随着间距L的增加, 极大值间距差ΔL逐渐增加, 极大值位置较为发散 (见图2) . (2) 同一频率下, 相邻两个极大值位置间距约为4.4 mm左右 (接近于波长的一半) .随着间距L的增加, 极大值所对应的电压幅值迅速地衰减。间距L大于100 mm时, 电压幅值基本不变 (见图3) .
上述结论解释如下:由文献[5]可知, 换能器S2表面处接收到信号为入射波形和反射波形叠加信号, 该信号的表达式为:
公式 (1) 中A是入射波的幅值, L是换能器S1和换能器S2的间距, λ是波长, 是信号源频率, 是初相位。从公式 (1) 式可知, 当换能器间隔L满足下式时
换能器S2表面为驻波的波节 (相对于声压来说则为驻波的波腹) , 输出电压为极大值。
又由公认的在空气中的声速计算公式其中t为测量时环境温度, 以摄氏度为单位, 本文实验过程中温度基本不变, 因此温度对波速的影响可忽略, 即在空气中基本不变。所以当信号频率为f时, 声波的波长为:
公式 (3) 代入公式 (2) 可得:.所以频率和频率同一干涉级的ΔL为:
由公式 (4) 可知:干涉级K越小, 频率和频率同一干涉级的ΔL越小, 即间距L较小时, 极大值位置较为集中。极大值为共振干涉极大值, 由于空气阻尼作用, 随着间距L的增大, 共振干涉极大值的幅值迅速减小。
2.2 谐振频率测量
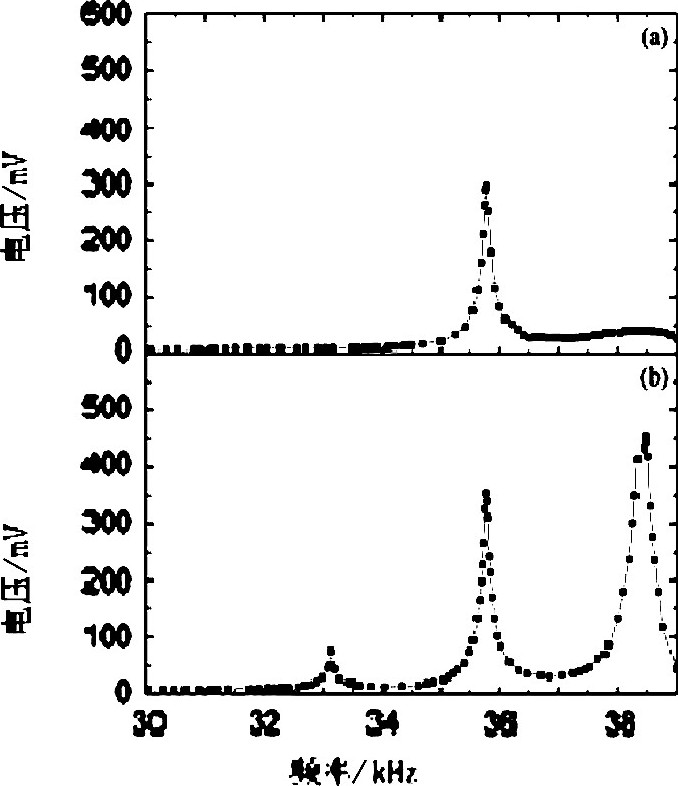
由图2可知:对33.012~39 k Hz频段内的信号来说, A点都为驻波波腹 (相对于声压来说则为驻波波节, 输出电压为极小值) , B点在有的频率下为驻波波节而有的频率下为驻波波腹。本文首先把换能器S2固定在图2所示的A点位置, 慢慢增加信号频率, 利用数值示波器测量相应输出电压, 得到电压幅值随频率变化曲线[见图4 (a) ].然后把换能器S2移动到B点位置, 重复上述过程, 得到此位置的电压幅值随频率变化曲线[见图4 (b) ].
从图4可以看到:换能器S2处于A点 (10.7mm) 时, 幅值-频率曲线只出现一个最大值点, 该点对应的频率为35.75 k Hz.当换能器S2处于B (30.0 mm) 点时, 幅值-频率曲线出现三个极值点, 三个极值点对应的频率分别为33.13 k Hz, 35.762k Hz, 38.475 k Hz, 其中频率为38.475 k Hz时输出电压幅值大于频率为35.762 k Hz时输出电压幅值。
对33.012~39 k Hz频段内的信号来说, A点为共振干涉极小值点。换能器S2处于A点时, 共振干涉引起的输出电压值极小, 即共振干涉对输出幅值的影响较小。因此图4 (a) 中极大值是系统谐振引起的, 即极大值对应的频率为系统的谐振频率 (35.75 k Hz) .当换能器S2处于B点时, 换能器S2输出电压既受共振干涉增强的影响, 同时还受系统谐振的影响, 所以图4 (b) 中出现的三个极值点。利用文献[5]所述的分析方法发现, 极大值对应频率由38.475 k Hz减小到33.13 k Hz, 波长倍数改变近似于半个波长, 进一步证实了图4 (b) 中的两个极值点 (对应频率是33.13 k Hz和38.475 k Hz) 是共振干涉引起的。图4 (b) 中间的峰对应频率 (35.762 k Hz) 与图4 (a) 中极大值对应的频率 (35.75 k Hz) 几乎相同。由于系统谐振频率是唯一的, 故图4 (b) 中间的峰对应的频率是系统的谐振频率。由于33.13 k Hz和38.475 k Hz都远偏离35.762 k Hz, 声强主要受信号频率影响, 而声强正比于信号频率的二次方, 故33.13 k Hz对应输出幅值远小于38.475 k Hz对应输出幅值。
由于图4 (b) 中38.475 k Hz对应的输出电压大于35.75 k Hz对应的输出电压, 由上面分析可知38.475 k Hz并不是系统的谐振频率。在谐振频率实际测量过程中, 如果换能器S2位置选择不恰当, 学生会得到错误的结果或则对谐振频率测量存在困惑。当换能器S2处于共振干涉极小值 (对33.012 k Hz~39 k Hz频段内的所有信号) 的位置 (间距L较小) 时, 共振干涉增强对输出幅值的影响基本可以忽略。当间距L较大时, 如果谐振引起的电压幅值远大于共振干涉增强引起的电压幅值, 也可利用常用的谐振频率确定方法确定谐振频率。
换能器S2与换能器S1的间距L分别是10.7mm (a) 和30.0 mm (b) .
3 结论
从实验结果得到如下结论: (1) 两个换能器间距L较小时, 不同频率下换能器S1的输出电压极大值位置是收缩的。随着间距L增加, 输出电压极大值位置逐渐发散; (2) 换能器S2处于共振干涉极小值 (对33.012~39 k Hz频段内的所有信号) 的位置时, 输出电压-频率曲线仅有系统谐振引起的极大值, 共振干涉的影响基本可以忽略; (3) 测量谐振频率时, 换能器S2应处于共振干涉极小值的位置或则共振干涉增强引起的电压幅值远小于系统谐振引起的电压幅值。
参考文献
[1]黄笃之。普通物理实验[M].长沙:湖南科学技术出版社, 1995.
[2]丁永文, 王玉新, 霍伟刚。大学物理实验[M].大连:辽宁大学出版社, 2017.
[3]陈洁。声速测量实验有关问题的研究[J].物理实验, 2008, 28 (6) :31.
[4]董正超, 方靖淮, 朱兆青, 等。大学物理实验[M].苏州:苏州大学出版社, 2011.
[5]刘勇, 张建国, 张盛源。超声波测量声速实验中谐振频率的确定[J].高等函授学报:自然科学版, 2012, 25 (4) :75-77.
[6]孙航宾, 黄笃之, 张禹涛。声速测量实验假象的探讨[J].大学物理实验, 2011 (4) :50-52.
[7]竺江峰。探究性学习在声速测量实验中的运用[J].大学物理实验, 2015 (2) :121-124.