
一、引言
自 20 世纪 90 年代以来区域市场中不乏有合作现象。传统的区域经济合作重点关注国家间存在的经济上的互补性和互利性,具体因素包括:国家间的双边或多边的协议;降低生产中的运输成本从而形成一体化;区域中的政治因素或其他的非经济因素的相互影响。Riezman(1985)认为关税同盟与核心的关系中有约束力的协议,从而分享区域经济合作的收益。孙大为和刘人境等(1998)分析了区域经济合作现象的内在核心,指出区域经济一体化的形成是多国或多成员达成共同认可的有约束力的协议,并可以分享合作博弈带来的收益。Ferreira(2000)考虑区域间经济差距的政策,发现财政政策、基础设施投资等扶持性政策的效果有限。而在当今的区域经济发展中,人才资源成为区域发展的最活跃的生产要素,人们也越来越认识到它的重要性;但是人才资源有着难培养、投资周期长、花费高和不稳定的特点,使得区域经济发展中常常遇到人才资源短缺困境。王锐兰和顾建强等人(2006)利用进化博弈理论,分析了区域创新人才的流动行为,并对在不同外在干扰下创新人才的流动行为进行了新的探讨。孙冰和安子鹏(2006)根据发达和不发达地区的博弈比较,认为不发达在人才竞争中具有一定优势,并可以通过政策巩固优势。窦开龙(2008)用博弈的方法来分析西部民族地区青年人才流失的原因,提出留住人才的具体措施,来解决对西部民族地区经济发展的人才危机。周洁(2009)依据人才市场的作用机制也不够完善,建立各地政府之间相互博弈模型,认为长三角地区应从政治和信息层面建立人才等方面经济合作的立法和执法框架。钱士茹和左瑞(2011)采用合作博弈方法,研究了不同区域间的人才资源的开发和共享,提高人才利用的效率。熊正贤和吴黎围(2013)根据西部区域文化产业上竞争过度现象,利用竞合博弈分析出西部区域在文化产业合作的可能性。
显然,当前的研究更多地是以区域或区域政府做为主体的宏观层面分析,这种研究不能体现人才资源在区域经济发展中所起影响作用的微观动因,特别是区域间人才开发中的合作问题。文章利用黑箱原理,基于完全信息下的动态博弈,尝试从微观经济角度,来讨论区域内各个企业人才资源的合作开发,以探寻企业人才资源配置的策略选择。同时,这种策略选择也将会解决区域人才短缺,促进企业所在区域的经济发展。
二、博弈的基本假设和模型建立
1. 博弈模型的假设目前我国各地经济开发区很多,宏观层面上,这些区域的经济发展的管理和决策大都是各个区域的行政主体;但是在微观层面上来讲,人才合作共享这属于企业内部的管理和决策。
区域内部的企业才拥有真正的决策权。通常区域 I 内有 1 或者N 个企业,它们可能属于进行上下游的同一条产业链或者属于在技术上和生产上类似或相关的产业群,在企业人才合作上已经有了最基本的条件。
假设 1:利用黑箱原理,不管区域 I 是指单个区域还是多个不同区域,都能被看成是合作博弈中可信的、可约束条件的一部分,从而使得分析不失一般性。
假设 2:经济区域内某产业有 A、B 两个企业,如果任何一个企业独立进行人才开发的决策行为时,它们的人才开发成本和收益均是独自承担,并且人才培养的市场总收益和总成本都固定不变,为此 A 企业市场总收益和总成本分别为 R 和 CA。因此文章假定在区域 I 内 A 企业先完成人才的培养。
假设 3:A 企业和 B 企业皆为理性经济人,目标都是追求自身企业的利益最大化;在企业中人才可以通过流动合作,或者通过独自培养获得。
假设 4:B 选择人才合作,那么区域内存在一种有约束力的协议,使得企业双方博弈结果是由博弈的联合理性决定,而不是个体理性决定。同时这种有约束力的协议,一般由当地区域政府主导,政府主导政策提供约束和保障。
假设 5:R 为获得的整个人才资源的收益;CA为 A 企业单独培养人才所支付的成本,Cd为 A 企业阻止 B 企业进入市场的成本,RS为 B 企业进入导致 A 企业的利润损失。
假设 6:RB为 B 企业人才资源提供的市场总收益,CB为 B企业单独培养人才所支付的成本。CG为 B 企业在不独自培养人才的情况下,支付 A 企业进行人才合作的费用;通常也是在政府主导下具体进行的有约束力协议的内容之一。
如此假设是基于现实的三个方面考虑:
第一方面,企业间的交易需要诚信作为基础,而区域政府(或政府) 和法律是交易诚信的保障。
第二方面,人才合作不仅增加企业的利润,而且直接增加区域政府的收入;同时也会繁荣区域内的经济,给官员的升迁带来一定正面影响,因此人才合作必定得到区域政府鼓励。
第三方面,区域政府的政策随着改革将会变得更加公开透明,并可以进一步增加政府的公信力。
前两个方面满足约束力的要求,最后一个满足完全的要求,因而文章采用完全信息下的动态博弈。
2. 博弈模型的建立
在区域 I 中,假设只要有一个企业人才培养或者开发成功,其他企业可以选择人才开发,亦可以选择不开发;而原企业可能选择阻止人才合作也可能不阻止,阻止过程花费额外成本 Cd;在 A 企业不阻止的情况下,B 企业才会考虑是否进行人才合作。
因此整个博弈过程分为三个阶段:
第一阶段,在区域内部,首先 A 企业获得人才开发成功,这是人才合作的前提。对于 B 企业来讲,有两种策略选择,开发或不开发。如果没有开发,则 B 企业的净收益都是零,没有开发中受益,并且博弈结束;如果开发,则进入第二阶段博弈。
第二阶段,在 A 企业在知道 B 企业会开发的情况下,A 企业根据人才的开发成功自身利益的判断需要,以及阻止 B 企业获取人才的成本,综合考虑是否选择阻止策略;且 A 企业要根据阻止 B 企业进入的成本 Cd的高低,来决定是否阻止 B 企业获得人才资源。若 A 选择阻止,则其净收益为 R-CA-Cd且满足条件(R叟CA,R叟Cd)。其中 R 为 A 企业的市场总收益,CA为 A 企业单独进行人才开发的成本;B 企业净收益为-CB且 RB叟CB。
其中 RB为 B 企业在 A 企业存在条件下,单独进行人才开发时的市场总收益,CB为 B 企业单独进行人才开发的成本。如果 A企业的净收益 R-CA-Cd燮0,A 企业选择不阻止,则将会进入第三阶段博弈。
第三阶段,在 B 企业在区域政府管理者提供的强制约束条件下,选择与 A 企业人才合作,并交纳一定的合作费用 CG;A企业根据收到的合作费用 CG的高低与 B 企业在人才合作上进行利益分配的博弈同,即 B 企业选择分享 A 企业人才成果的情况下,A 企业会根据对未来成本收益的大小来决定人才合作谈判是否成功。若合作谈判不成功,则 B 企业的收益就等同于 B 企业独自开发人才时的收益 RB减去 B 企业的成本 CB,净收益为 RB-CB且 RB叟CB,并且人才合作为市场提供的总收益 R 不变的情况下,A 企业的收益为 R-CA-RS,RS为 B 企业进入市场后 A 企业的利益损失,它是由 A 和 B 企业进入开发人才时,B 企业分享人才的总收益造成。由于假定人才的总收益 R 不变,对于 A 企业来讲总会有 RS叟RB-CB的经济损耗。因此只要 B 进入人才市场时,无论谈判成功与否 A 企业都将有一个 RS利润损失。【1】
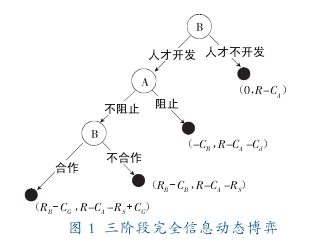
若合作谈判成功,则 B 企业的收益为 RB-CG,CG为 B 要支付给 A 企业的合作成本;A 企业的收益为 R-CA-RS+CG。此过程中假设谈判成本忽略不计。
三、博弈模型分析
1. 博弈结果文章的上述模型采用逆推归纳法来分析和求解。从第三阶段开始,首先考虑合作谈判时 B 和 A 企业的收益,在这个阶段,A 企业的最优选择是合作,其得益为 R-CA+CG-RS,因为在 CG在大于零的条件下总是存在 R-CA+CG-RS>R-CA-RS。对于B 企业的选择,则要比较 CB和 CG的大小 (共三种情况),然后再考虑第二阶段中 Cd阻止费用的高低,共分为当 CG-RS叟Cd和CG-RS<Cd两类分别进行讨论。
第一类,当 A 企业收益中存在 CG-RS叟Cd,即 A 企业的合作净得益大于阻止成本。
在此条件下,B 企业要比较成本 CB和支付给 A 企业的合作费用 CG,模型中是否具有纳什均衡,文章的研究将其分成三种情况讨论。
情况 1:当 CG<CB时。根据逆推归纳法,则 B 和 A 企业的收益满足其如下公式:RB-CG>RB-CBR-CA+CG-RS叟R-CA-RS叟(1)公式(1)成立,因此子博弈 (合作,非合作) 的第三阶段处具有纳什均衡。B和A 企业的均衡得益为(RB-CG,R-CA-RS+CG)。结合式(1)由此可知,子博弈 (开发-合作,阻止) 人才合作是双方企业的最优解。情况 2:当 CG=CB时。
此时,B 和 A 企业的收益满足其如下公式:【2】

公式(2)成立,则可以同时满足子博弈 (合作,非合作) 中第三阶段和第二阶段博弈,因而该条件成为 B 和 A 企业的双方谈判的破裂点,此时双方无论选择人才合作还是选择人才不合作对于 B 企业来讲收益相同,相当于独立开发。而对于 A 企业的得益相差很大,合作时 R-CA-RS+CG比非合作 R-CA-RS多出 CG。此处的最终结果取决于 B 企业的选择。因此,此处 A 和 B企业不存在纳什均衡。
情况 3:当 CG>CB时。根据逆推归纳法则,此时,B 企业和 A 企业的收益满足如下公式:【3】
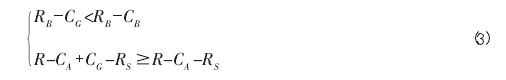
公式(3)成立,则子博弈 (合作,非合作) 中第二阶段有博弈均衡,B 和 A 企业的双方人才谈判破裂,此时双方企业选择不合作,B 和 A 企业的收益分别为 RB-CB和 R-CA-RS。
第二类,A 企业收益中存在 CG-RS<Cd,即 A 的合作净得益小于阻止成本。
根据逆推归纳法则,模型博弈 (开发-合作,不开发) 有子博弈纳什均衡时,B和A 企业的收益满足如下公式:【4】

公式(4)成立,模型博弈 (开发-合作,不开发) 在第三阶段有博弈纳什均衡,这不仅考虑 A 企业的合作净得益要小于阻止成本 Cd,还要考虑 B 企业的得益小于 B 企业进入市场后 A 企业的利益损失 CG<(1/2)RS;以及满足 CG<CB条件存在时,双方企业才会有合作均衡。
2. 结果分析根据上述分析区域内部的两个企业在不同的成本条件下,博弈出现以下几种结果:
第一种博弈结果,当 A 的合作净得益大于阻止成本 CG-RS叟Cd时,这意味着对于 A 企业来讲,合作博弈是存在最大收益,博弈是否具有均衡由 B 企业来均衡。此时如果满足 B 企业的人才共享成本小于企业的进入成本 CG<CB,即博弈双方未达到谈判破裂点时,双方就会存在博弈均衡,其最好的结果就是双方选择合作策略。当 A 的合作净得益要小于阻止成本 Cd, B企业的人才共享支付 CG<(1/2)RS,以及 CG<CB条件同时满足时,企业双方选择合作也是一个较优的选择策略。对于 A 和 B 两个企业来讲,这时的博弈均衡是一种双赢选择。不仅降低了进入企业 B 的人才投资成本,同时,人才拥有者 A 企业,可以获得一定的共享费用,增加了收益,减少了人才开发时的成本。此外,还鼓励了新企业进入该区域发展,从而对该区域的经济繁荣起到积极作用。
第二种博弈结果,当企业双方收益等于谈判破裂点时 (即人才的共享成本等于企业的进入成本),虽然 B 企业的得益与独自开发相同没有利润增加,但是 A 企业合作净利润没有发生变化,因此 B 企业有着选择与 A 企业合作与不合作的主动权,从而此处没有子博弈的纳什均衡。
第三种博弈结果,当企业双方收益超过谈判破裂点时,双方企业选择不合作,这是一个双输的结果。这就要求 B 企业从头开始培育自己的人才,一方面费时费力,另一方面可能影响B 企业的发展。对于 A 企业来讲,不仅没有共享费用,同时还因为 B 企业的进入,自身利益会受到白白损失。这将会导致只有很少的企业才会进入该区域内部生产,从而影响该区域经济的发展。
第四种博弈结果,上述几种双方合作博弈都是在区域政府提供的有约束力人才合作条件下进行,使得支付的人才合作费用和人才交流有确定性的保障,并且不需要相互取得信任的成本。否则,双方的合作博弈将在第一阶段就结束。因此,在完全信息下的合作博弈中,博弈的双方如何选择一个合适的人才共享费用是非常重要的,它直接影响着双方合作谈判的破裂点。同时博弈双方的合作得益不仅来自于双方的讨价还价,也受到区域可信的人才合作机制的影响。
四、结论和建议
区域经济发展中,人才资源是最重要的生产要素之一。文章基于微观角度,以企业的经营决策为出发点,利用黑箱原理和博弈工具,建立了采用完全信息下的人才合作的动态博弈模型。文章通过对模型的三个博弈阶段进行逆向归纳分析,讨论了形同或不同区域内两个企业间的人才资源合作时在各种情况下的净得益和阻碍成本。
从上述完全信息的几种动态博弈的结果分析中,可以得出如下两点结论:
一是在区域经济的发展中,人才合作时的成本以及对人才的合作机制成为区域管理企业可信程度都将会影响合作双方的博弈均衡。我国目前有很多区域的企业存在人才短缺问题,由于企业内部的人才资源的不一样,导致企业发展的差异。
二是如果在区域内制定企业共同遵守的经济发展制度,倡导人才合作,可以在一定程度上弥补人才短缺的现状,并促进该区域经济的繁荣和区域经济的交流。同时,人才如果在不同区域合作也能促进区域间的经济获得均衡的发展。
综合上述分析,文章针对区域的发展提出以下几点建议:
首先,区域政府应当鼓励企业间人才合作和共享,给予拥有人才的企业在科技研发的资金和企业发展的政策上的优惠政策,使得人才所在的企业减少采取阻止策略措施。
其次,在区域内经济发展中,制定和规范企业共同遵守的人才合作和人才交流机制,降低和规范人才合作共享时的费用,使得用人单位的人才共享成本降低到行业的合理水平。
再次,区域政府要在企业间建立商品交易和人才交流的等级信用机制和奖惩措施,引导和鼓励企业间人才合作。
最后,区域政府间应统一制定鼓励人才流动政策,建造人才合作流动的平台,采取措施鼓励和吸引人才到区域内工作,从而扩大人才的来源,有利于企业进入这些区域。
【参考文献】
[1] Riezman R. Customs unions and core [J].Journal of International onomics,1985(19).
[2] Afonso Ferreira. Convergence in Brazil:recent trends and long-run prosp-ects [J].Applied Economics,2000(4).
[3] Behrman,J.R,Birdsall,Nancy. The Quality of Schooling:Quantity Alone isMisleading [J].The American Economic Rezpietu,1984.





