
钢筋混凝土结构分析分为整体式、组合式、分离式三种有限元模型。分离式模型计算精度高,但是该模型需要将钢筋布置在混凝土单元边界,网格要求高,计算时间较长。该模型多用于混凝土构件的力学分析。如田力等利用分离式模型分析了钢筋混凝土柱在冲击荷载作用下的破坏模式。组合式模型钢筋布置相对灵活,但是难以模拟钢筋滑移对裂缝形态的影响。对于配筋较多、结构较大的模型,学者也做了大量研究。如吕西林等用实体单元模拟剪力墙结构,将钢筋弥散于四节点等参单元中,分析了顶层加速度反应时程和位移时程。左晓明等应用整体式有限元模型分析桥墩试验,建议将剪力传递系数 η 按照函数模型取值,以保证计算结果的准确性。周锡元等在分析钢筋混凝土框架剪力墙结构时,提出改进的多垂直杆单元模型,并与试验相对比,验证了方法的有效性;夏桂云等对于框架剪力墙结构建立了连续化模型,并给出了理论解。Ean Tat Ooi等在比例边界有限元方法中采用局部网格重构来模拟混凝土开裂,并考虑钢筋和混凝土之间的相互滑移。龙渝川等结合分离式和组合式提出新的嵌入式滑移模型,利用粘结单元表面位移差模拟钢筋滑移。
本文使用整体式模型,定义了混凝土开裂后,裂缝处剪应力和剪应变的本构关系。本构关系中考虑到钢筋和混凝土两种材料的共同作用。与传统意义上整体式模型相比,本文考虑了钢筋对混凝土开裂的影响。通过与钢筋混凝土简支梁的剪切破坏试验相比较,验证了该方法的有效性。根据试验体的实际尺寸和配筋情况,分别建立输入配筋率的分离式模型和优化整体式计算模型,并将两组计算结果分别与试验结果对比。结果表明:优化整体式模型能很好的模拟试验,所采用的本构方程定义准确,同时比分离式模型计算速度快。最后,应用优化方法进行实际工程的计算,结果满足精度要求且计算速度快,具有非常好的应用价值。
1、 试验概述
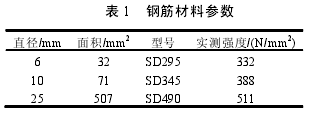
计算模型为某简支梁试验体,总长 4300mm,高 300mm,宽 160mm。试验共设计 10 个加载装置,并在相应位置设置加载板和支承板,试件及加载位置见图 1。沿轴线方向将试件分为四个区域,其中区域 B为试验段,该区域箍筋直径为 6mm,其余区域为 10mm。梁截面上下各三根直径为 25mm 的主筋,保护层厚 40mm。钢筋材料参数见表 1,其中 SD295 是日本带肋钢筋型号,表示带肋钢筋设计抗拉强度为 295MPa。
混凝土抗压强度为 32.7MPa,抗拉强度为 2.79MPa,粗骨料直径为 13mm。
2、 有限元模型及计算
2.1 几何模型及网格划分
分离式模型采用八节点六面体单元模拟混凝土,二节点杆单元模拟钢筋。杆单元和六面体单元共用节点。加载板和支撑板采用四节点壳单元来模拟。壳单元与六面体单元共用节点。根据主筋和箍筋的配筋位置,将单元网格沿 Y 轴方向划分 4 层,沿 Z 轴方向划分 8 层。混凝土网格和内部钢筋。
整体式模型也采用六面体单元模拟混凝土。与分离式模型不同的是,划分网格时无需考虑钢筋位置,只需按照体积配筋率将钢筋输入到六面体单元中,从而减少单元数目。单元网格沿 Y 轴方向仅划分 1 层,沿 Z 轴方向划分 8 层,同时减少了沿 X 轴方向的网格数目,如图 2b。
在对六面体单元输入配筋率时,按照 3 个方向分别输入,每个方向的配筋率是由该方向配置的钢筋体积除以区域的总体积得到。主筋配筋沿 X 方向,箍筋配筋沿 Y 方向和 Z 方向。考虑配筋位置,由于梁腹部的 4 层单元没有主筋和 Y 方向箍筋穿过,所以将每个区域分为腹部和边缘两部分。腹部单元是指沿 Z轴方向中间 4 层单元,边缘单元是指其余的 4 层单元。六面体单元 3 个方向的体积配筋率的大小见表 2。
2.2 本构关系
混凝土应力应变关系如图 3。混凝土在受压状态下的应力应变关系曲线采用修正 Ahmad模型。混凝土受拉开裂之前是线性关系,开裂之后通过双线性本构关系模型来描述拉应力随着裂缝的增大而减小的关系,如图 4。断裂能计算公式为式(1):


式中:GF为断裂能;maxd 为混凝土的最大骨料直径;ckf 为混凝土单轴抗压强度标准值。
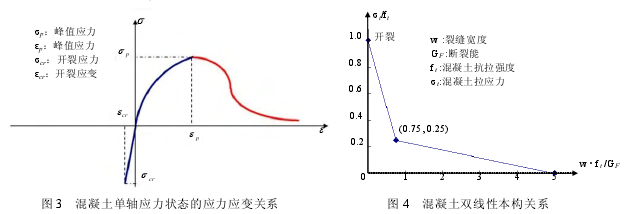
反复荷载作用下混凝土的应力应变关系采长沼·大久保模型。三轴应力状态下的混凝土破坏准则选用四参数的 Ottosen 强度准则模型。钢筋的应力应变关系采用基于 von Mises 屈服准则的双线性随动强化模型,屈服后的刚度降为初始刚度的 1/100。
如何模拟裂缝面间的剪力传递方式一直是一个难点,学者做了大量研究。本文选用长沼一洋模型。考虑开裂方向、裂缝宽度、截面配筋率、钢筋屈服强度等多方面影响,定义剪切面内的剪应力ntt 与剪应变ntg 的关系。计算公式为式(2):

式中:ntt 为沿着裂缝表面方向的剪应力;ntg 为沿着裂缝表面方向的剪应变;te 为与裂缝垂直方向的应变,与裂缝宽度有关;ntmaxt 为沿着裂缝表面方向的最大剪应力;f 为裂缝方向与钢筋轴向所成的夹角;xe ,ye ,xyg 分别为混凝土的正应变及剪应变;dut 为在存在横断裂缝面的钢筋情况下的直接剪切强度;C 为与应力应变关系曲线形状有关的参数;r为截面配筋率;sys 为钢筋屈服强度;ns 为裂缝法线方向的混凝土应力。
2.3 加载方式与边界条件
在有限元计算中,分别在各个荷载板处施加竖向荷载 P1和 P2,并始终保持 P2=40/27P1,直至构件发生破坏。约束左面支座处节点的 x,y,z 方向的位移,约束右面支座处节点的 y,z 方向位移。
3、 模拟结果分析
3.1 荷载位移曲线
计算过程中的位移监测点位于梁下表面对称位置。竖向荷载 P1和监测点竖向位移关系曲线与试验极限荷载,见图 5。可以看出,两条曲线形状相似。监测点竖向位移达到 5.2mm 之前,整体式模型曲线位于分离式模型曲线上方,说明整体式模型比分离式模型的刚度稍大。
计算初期,曲线近似为线性关系,可认为模型处于弹性阶段。到 P1=48kN 时,两条曲线都有明显的转折,表现出塑性性能。分析试验加载过程,此时试验体上出现较为明显的斜裂缝,计算结果与试验结果相符合。优化计算在 90kN 之后,曲线趋于水平,说明此时模型已经丧失承载力。分离式模型在 91kN 之后也表现出类似的情况,并且在监测点位移达到 5.2mm 之后,两条曲线基本重合,说明两个模型强度值接近。
试验中的极限荷载为 89kN,两个模型的计算结果分别比试验结果大 1.1%和 2.2%,都具有很好的精度。
3.2 各监测点位移
试验各监测点位移如图 6 所示,两组有限元计算结果。试验分别记录第一组明显裂缝,以及两条较宽裂缝出现时刻的各个监测点的位移。由试验数据可以看出,各点位移不对称,由于试验区段的配筋较弱,试验区段的位移稍大。在 P1=80kN 的时候试验体下表面对称位置的竖向位移为 5mm,有限元模型计算结果中,整体式模型刚度要大一些,位移稍小。试验区段计算结果与试验拟合较好。
3.3 裂缝开展过程
图 8 为有限元模型计算的裂缝图,图 9 为试验的裂缝图。由图 8 可以看出,加载至 P1=48kN 时,梁腹中位置出现一组斜裂缝,之后逐渐向外发展。加载至 P1=62kN 时,模型已出现大面积斜裂缝,其中腹中位置的一条斜裂缝宽度较大。随着荷载增加,模型上出现另外一条较宽裂缝,该裂缝首先水平向右开展,随后斜向上延伸。加载至 P1=80kN 时,已经明显能看出两条裂缝的走向。由图 9 可以看出计算结果与试验结果吻合非常好。
3.4 计算效率对比
分离式模型单元数目为 4625 个,计算所需时间为 1537 秒;整体式模型单元数目为 591 个,计算时间为 113 秒。可以看出整体式模型大量减少单元数目和计算时间,显著提高效率。
4、 算法应用
4.1 工程背景
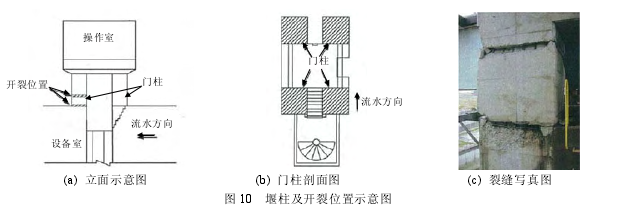
应用所提出的优化方法对日本某堰工程中的某个堰柱进行非线性分析。堰柱底部是设备室,顶部是操作室,门柱位于设备室和操作室之间。2004 年日本发生里氏 6.8 级地震。在地震作用下,门柱发生开裂现象,开裂位置如图 10 所示。
4.2 有限元模型
有限元模型可分为操作室板、门柱以及设备室三部分,如图 11a。本文重点分析门柱,将操作室部分简化处理,底板以上的永久荷载折合成质量附加到板上。门柱截面为正方形,边长 1750mm。柱子设有连梁,梁高 1670mm,如图 11c 所示。混凝土由六面体单元模拟,并根据实际配筋在相应单元中输入体积配筋率。本构关系采用本文提出的优化方法。模型边界条件为固定底层节点三个方向的平动自由度,固定设备室侧面节点的水平自由度。采用 pushover 静力拟动力法对结构进行单向推覆分析。
4.3 结果分析
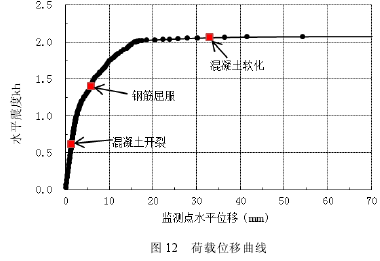
位移检测点位于操作室板上表面中心位置处,如图 11a 所示。该点水平位移与震度 Kh 的关系曲线如图 12 所示,红点位置表示混凝土开裂,钢筋屈服,以及混凝土软化时刻。可以看出,混凝土开裂以后,结构明显表现出非线性行为;在震度达到 2.1 左右,混凝土出现软化,结构发生破坏。图 13 描述了门柱裂缝情况,红线表示裂缝位置,绿色部分表示混凝土发生软化的单元。可以看出,门柱的计算开裂位置与实际开裂位置较为接近。
5、 结论
通过对简支梁试验以及工程实例进行数值模拟分析,可以得到以下结论:
(1) 本文采用长昭一洋模型模拟裂缝间的剪力传递方式,并通过试验和数值计算证明了该方法的合理性。
(2) 有限元计算结果显示模型首先在下表面的剪弯区出现弯曲垂直裂缝,然后斜向延伸,在 P1=80kN时形成两条较宽的主裂缝,是典型的斜截面受剪破坏形态,裂缝形状与开展过程均与试验相符合。
(3) 有限元计算得到的两条荷载位移曲线形状相似。试验极限强度值为 89kN,整体式模型计算的极限强度值为 90kN,分离式模型为 91kN。两种方法精度相近,但是整体式模型计算速度更快。
(4) 门柱 pushover 计算分析结果中的开裂位置与实际工程基本相同。优化计算方法克服了以往对含有复杂配筋的钢筋混凝土结构进行整体分析时,难以精确计算细部破坏的困难。拓宽了有限元软件的适用范围,为数值模拟方法的更加普及提供了帮助。
参考文献:
[1] 田力, 朱聪, 王浩等. 碰撞冲击荷载作用下钢筋混凝土柱的动态响应及破坏模式[J]. 工程力学, 2013, 30(2): 150-155.
[2] 吕西林, 吴晓涵. 抗震耗能剪力墙非线性有限元时程分析[J]. 同济大学学报: 自然科学版, 1996, 24(5): 481-486.
[3] 汪梦甫, 周锡元. 钢筋混凝土框架—剪力墙结构非线性地震反应实用分析方法的研究[J]. 土木工程学报, 2002, 35(6):32-38.
[4] 左晓明, 叶献国, 杨启龙. 钢筋混凝土非线性有限元中剪力传递系数及其数值试验[J]. 建筑结构, 2009 (3): 14-16.
[5] 夏桂云, 欧见仁, 李传习, 等. 考虑剪力墙剪切变形影响的框架-剪力墙结构分析[J]. 工程力学, 2013, 30(6): 217-222.





