
引 言
箍筋约束混凝土在轴心受压下的峰值参数反映了构件的承载和变形能力,对本构关系确定有着重要的作用。研究表明在混凝土构件中配置一定数量的箍筋能有效地提高承载能力并改善变形能力。目前国内外对于普通箍筋约束混凝土构件研究已经有大量成果,但对于高强箍筋约束混凝土构件研究成果较少,大多数峰值参数计算方法考虑的变量较少,不能全面反映钢筋构造及构件尺寸对峰值参数的综合影响。
Cusson和杨坤给出了考虑因素较为全面的峰值参数计算方法,但是箍筋应力取值存在一定缺陷,而且只对参与回归的试件进行了计算值和试验值的验证。
本文选取 Cusson的 26 个(235 mm×235 mm×1400mm)高强箍筋约束混凝土柱建立计算方法,并制作 9个(250mm×250mm×850mm)高强箍筋约束混凝土柱对该计算方法进行补充验证。
1 建立峰值参数计算方法
1.1 建立回归公式
1.1.1 有效侧向约束应力
在箍筋的侧向约束作用下,混凝土内将产生与箍筋约束平衡的侧向约束应力使混凝土处于多轴受压状态,从而在一定程度上提高混凝土轴心受压柱的承载力和延性。在配置有矩形箍筋的矩形截面中,基于箍筋约束力与混凝土侧向约束力平衡条件,混凝土侧向约束应力 fl为:【1】

式中:fhcc为约束混凝土峰值点对应的箍筋应力;s 为箍筋间距;cx和 cy分别为 x、y 方向最外围箍筋轴线间距离;Ashx和 Ashy分别为 x、y 方向箍筋的横截面面积之和。
由于约束混凝土内部拱作用,侧向约束应力 fl只充分作用在约束混凝土核心面积一定范围内,见图1。Mander引入有效约束系数 ke对侧向约束力进行修正,ke为核心混凝土有效约束面积与核心混凝土面积比,反映了配筋形式和截面尺寸对混凝土的约束效果。修正后得到的有效侧向约束应力 fle见式(2)。【2-3】
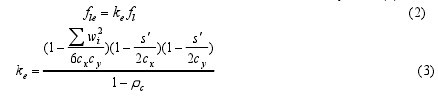
式中:wi为第 i 个相邻纵筋之间的横向净距;s?为箍筋净间距;ρs为纵筋核心配筋率。
fle与 fco(fco为未约束混凝土峰值应力)的比值体现了箍筋对约束混凝土的约束效果,其值越大说明箍筋对混凝土约束作用越明显。对于方形箍 cx=cy=c、Ashx=Ashy=Ash,联立式(1)~(2)可得式(4)。【4】
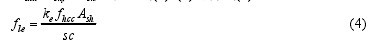
1.1.2 箍筋应力
根据文献[6],对于方形箍、棱形箍、八角形箍和井字形箍,定义其 Ash分别为 2、3.41、3.61、4.67 倍Asolo,Asolo为单肢箍面积。式(4)中,要得到有效侧向约束力 fle,还需要知道约束混凝土达到峰值点时对应的箍筋应力 fhcc。众多学者是通过在各肢箍筋中点处贴应变片来获取箍筋应力。研究表明,矩形箍应力沿周边分布不均匀,对角线方向约束力最大,箍筋各肢中部约束力最小。若以箍筋各肢中点处测得的应变作为箍筋应变计算 fhcc,则可能导致结果不准确。且复合箍约束混凝土在峰值点时其内外箍筋应力发展程度不一致,简单取算数平均作为平均箍筋应力不能合理地反映箍筋对核心混凝土的约束情况。这就要求提出一种能合理估计在峰值荷载时箍筋应力的计算方法。约束混凝土达到峰值点时,方形箍截面箍筋应变可表示为:【5】

式中:εhcc为约束混凝土峰值点对应的箍筋应变;εcc为约束混凝土峰值应变;fcc为约束混凝土峰值应力。
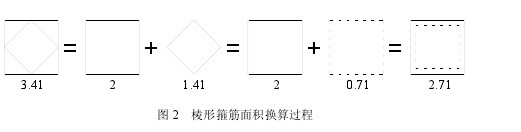
式(5)中,对于 26 个轴心受压试件 εhcc、fle未知,与式(4)联立,加上箍筋本构关系,可得到方形箍峰值点对应的箍筋应力,见式(6)。若 fhcc大于屈服强度 fyv,则取 fhcc等于 fyv。将 fhcc代入式(4)可以得到有效侧向约束力 fle。对于复合箍筋,由于内肢箍与外肢箍在峰值点应力发展程度不一致,采用面积换算法将其等效为方形箍进行计算。以棱形箍为例说明,棱形箍 Ash=3.41Asolo,将其视为由外围箍 Ash1=2Asolo和内部箍Ash2=(3.42-2) Asolo组成,如图 2;将 Ash2乘以换算系数 β=0.5,β 为内部箍同外围箍的约束面积之比,此时换算后的 Ash=Ash1+βAsh2;使用换算后的 Ash取代原 Ash进行式(6)箍筋应力计算;同方形箍,若 fhcc大于箍筋强度 fyv,则取 fhcc等于 fyv。经计算得棱形箍、八角形箍、井字形箍的换算系数 β 分别为 0.5、0.7、0.3,得到的换算 Ash分别为 2.71、3.13、2.80 倍 Asolo。【6】
【图2】

1.1.3 回归公式
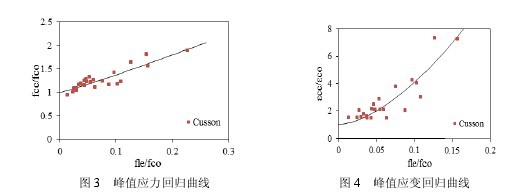
对 26 个约束混凝土峰值应力和峰值应变提高程度进行回归分析,自变量均取为 fle/fco,如图 3~4。可得到式(7)~(8)函数表达式,fco为未约束混凝土峰值应力,εco为未约束混凝土峰值应变,根据《混凝土结构设计规范》(GB50010-2010)取得。在计算和验证过程中考虑到混凝土试件之间的尺寸效应,对标准圆柱体混凝土峰值应力取 ACI 建议值 0.85 折减系数;对标准立方体混凝土试件峰值应力取 0.85×γ折减系数,γ为标准圆柱体与标准立方体混凝土抗压强度比值,CEB-FPI 给出标准立方体抗压强度在 60MPa 以下时γ=0.79。
由回归公式可知:约束效果良好的构件(fle/fco>3%),箍筋能有效提高其峰值应力、峰值应变,提高程度均大于 10%;约束效果一般的构件(1.2%<fle/fco<3%),箍筋对其峰值应力提高影响不大,但能够一定程度提高其峰值应变;约束效果较差的构件(fle/fco<1.2%),箍筋对其峰值应力、峰值应变的提高程度不明显,均小于 10%。【图3-4】
1.2 通过回归公式计算峰值参数
在式(7)~(8)中,要计算峰值参数 fcc与 εcc,需要知道约束混凝土有效侧向约束力 fle,但是在求解 fle与fhcc的联立方程式(4)~(5)中包括未知量 fcc与 εcc,无法进行。所以本文通过迭代方法来计算峰值参数 fcc与 εcc。
对于复合箍筋取换算面积 Ash进行计算,迭代步骤如下:① 假设在峰值点箍筋达到屈服强度,即取 fhcc=fyv;② 利用式(4)计算 fle;③ 利用式(7)~(8)分别计算 fcc、εcc;④ 将步骤③得到的 fcc、εcc代入式(6),计算得到新的箍筋应力 fhcc;⑤ 重复②~④,直到 fhcc收敛或 fhcc>fyv,结束迭代;⑥ 将收敛的 fhcc或者 fyv代入式(4)计算 fle,最终通过式(7)~(8)计算 fcc、εcc。
2 试验验证
2.1 试件设计
为了对上述方法进行验证,设计并制作了约束混凝土柱共 3 组,每组 3 个试件。试件截面尺寸为250mm×250mm,高度为 850mm,配置 6 根直径均为 12mm 的纵筋。箍筋形式为矩形箍,直径均为 5mm。
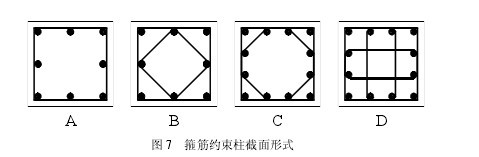
保护层厚度 c=25mm。具体设计参数及部分试验计算结果见表 1。
2.2 计算值和试验值对比
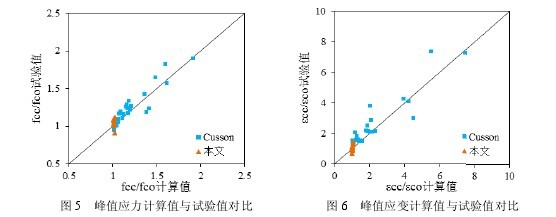
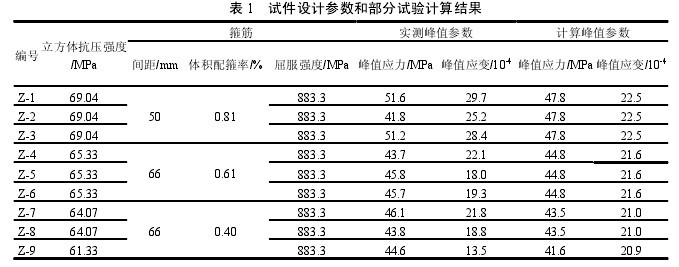
分别用此方法对文献[6]的 26 个约束混凝土柱和本文的 9 个约束混凝土柱的峰值参数进行计算,得到峰值参数提高程度的计算值。再将计算值与试验值进行对比,如图 5~ 图 6。
由图可知:约束混凝土柱的峰值应力、峰值应变计算值与试验值均符合程度较好。其中 9 个约束混凝土试件均为方形箍,约束作用小而且范围窄,故在图中计算值间隔紧密,试验值呈现出一定离散性。【5-6】【表1】
3 计算方法在高强箍筋中的应用
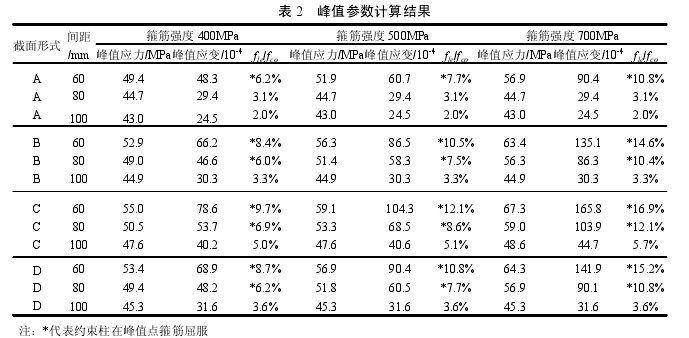
基于上述轴心受压构件承载力与延性分析方法,定量分析在其他条件不变的情况下采用高强箍筋代替普通箍筋对约束混凝土峰值参数的影响。在满足《混凝土结构设计规范》(GB50010-2010)要求前提下设计截面尺寸为 500mm×500mm,截面形式分别为方形箍、棱形箍、八角形箍和井字形箍等 4 种形式箍筋约束柱,如图 7 所示。每种截面形式考虑箍筋间距(60mm、80mm、100mm)、箍筋强度(400MPa、500MPa、700MPa)等参数,各设计 9 个试件,共 36 个试件。分别按上述方法计算各约束柱的峰值参数,计算结果见表 2。
由结果可知:1、不同截面形式中箍筋间距为 60mm 的柱在峰值点时箍筋全部屈服。其中箍筋强度为500MPa 的柱峰值应力和峰值应变较箍筋强度为 400MPa 的柱分别提高了 5.02%~7.33%和 25.69%~32.70%,箍筋强度为 700MPa 的柱峰值应力和峰值应变较箍筋强度为 400MPa 的柱分别提高了 15.32%~22.37%和87.24%~111.05%,其中复合箍峰值参数提高程度均大于方形箍;2、箍筋间距为 80mm 的试件在峰值点时复合箍箍筋屈服,方形箍箍筋未屈服。故复合箍箍筋强度得到充分发挥,提高箍筋强度对其峰值参数影响较大。但对于方形箍在峰值点箍筋未屈服,提高箍筋强度对其峰值参数影响不大;3、箍筋间距为 100mm试件在峰值点箍筋均未屈服,提高箍筋强度对其峰值参数影响不大。
由此可得结论:当箍筋对核心混凝土约束效果很好(fle/fco>6%),即箍筋应力能充分发挥时,将箍筋强度从 400MPa 提高至 500MPa 甚至 700MPa 能有效地提高约束混凝土柱的峰值参数。且约束效果越好峰值参数提高程度越明显。在本文中,配有间距为 60mm 八角形箍的柱使用 700MPa 箍筋替代 400MPa 箍筋后,其峰值应力提高 22.37%,峰值应变提高 111.05%,在提高其承载力同时大大改善了其延性。但当箍筋间距过大(本文中箍筋间距超过 100mm 时),即箍筋对核心混凝土约束效果较差时,提高箍筋强度对峰值参数的提高基本无贡献。【图7.表2】
4 结论
(1) 考虑各种基本因素对约束混凝土柱的影响,在采用面积换算法计算箍筋应力的基础上建立了约束混凝土峰值参数的计算方法,计算结果与试验结果较吻合。
(2) fle与 fco的比值综合体现了箍筋对约束混凝土柱的约束效果。约束效果良好的构件(fle/fco>3%),箍筋能有效地提高其峰值应力、峰值应变,提高程度均大于 10%;约束效果一般的构件(1.2%<fle/fco<3%),箍筋对其峰值应力提高影响不大,但能够一定程度提高其峰值应变;约束效果较差的构件(fle/fco<1.2%),箍筋对其峰值应力、峰值应变的提高程度不明显,均小于 10%。
(3) 基于本文峰值参数计算方法,计算得出当箍筋对核心混凝土约束效果很好时(fle/fco>6%),将箍筋强度从 400MPa 提高至 500MPa 甚至 700MPa,能有效提高约束混凝土柱的峰值参数。且约束效果越好峰值参数提高程度越明显;对于 fle/fco<6%的构件,在箍筋强度为 400MPa 时提高箍筋强度对约束混凝土柱峰值参数基本无影响。
参考文献:
[1] 李惠, 周文松, 王震宇, 徐欣, 于大忠. 约束及无约束泵送高性能与超高性能混凝土力学性能试验研究[J]. 建筑结构学报, 2003, 24(5): 58-71.
[2] 支运芳, 牛绍仁. 箍筋约束高强砼短柱受力性能的试验研究[J]. 重庆建筑大学学报, 1996, 18(2): 53-60.
[3] 胡海涛, 叶知满. 复合箍筋约束高强混凝土应力应变性能[J]. 工业建筑, 1997, 27(10): 23-28.





