
百年大计,教育为本。在中华民族实现伟大复兴的今天,我们更应该重视教育。新课程改革已经实施几年了,从教学上看,这次课程改革所带来的变革主要体现在两方面:一是教学内容的变化;二是教学方式的转变。教学方式的转变主要是要加强学生创造性思维。那么,如何在教学中培养学生的创造性思维呢?
一、什么是创造性思维及特征
所谓创造性思维,是指带有创见的思维。
具体地说,是指学生在学习过程中,善于独立思索和分析,不因循守旧,能主动探索、积极创新的思维因素。它具有以下几个特征:
一是独创性———思维不受传统习惯和先例的禁锢,超出常规。在学习过程中对所学定义、定理、公式、法则、解题思路、解题方法、解题策略等提出自己的观点、想法,提出科学的怀疑、合情合理地“挑剔”。
二是求异性———思维标新立异,“异想天开”,出奇制胜。在学习过程中,对一些知识领域中长期以来形成的思想、方法,不信奉,特别是在解题上不满足于一种求解方法,谋求一题多解。
三是联想性———面临某一种情境时,思维可立即向纵深方向发展;觉察某一现象后,思维立即设想它的反面。
四是灵活性———思维突破“定向”、“系统”“规范”“模式”的束缚。在学习过程中,不拘泥于书本所学的、教师所教的,遇到具体问题灵活多变,活学活用活化。
二、如何培养学生的创造性思维
(一)巧设悬念,建立创造思维情境
数学教学过程离不开一定的数学情境。针对初中生的年龄阶段,好奇、好动的性格,数学情境对学生注意力的吸引、积极性的提高、创造欲的诱发,具有极其重要的作用。因此,在教学活动中,教师应该巧妙地设置悬念,调动学生的积极性,吸引学生参与到教学活动中来,引导学生进行思考,激发学生的求知热情。
例如,在讲“勾股定理的应用”时,教师可以设计这样一个问题:《九章算术》有一勾股定理名题:“今有池方一丈,葭(jiā)生其中央.出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何.”教师通过十二世纪印度有一勾股定理名题:有一根木柱,木柱下有一个蛇洞,柱高15尺,柱顶上有一只孔雀,孔雀见一条蛇游来,现在与洞口的距离还有三倍柱高,就在这时,孔雀猛地向蛇扑过去,问在离蛇洞口多远孔雀与蛇相遇?(假定孔雀与蛇的速度相同)教师通过这样的问题情境,激发了学生的求知欲望,开始积极思考,寻求答案。这样一来,既有效地提高课堂教学效率,也能很好地培养和发展学生的思维能力。
(二)培养学生敏锐的观察力
观察在人类的各项活动中都占有重要的地位,对中学生来说,没有观察就没有学习。“知己知彼,百战不殆”,只有对问题进行全面的、详细的、准确的、系统的观察,才能有所发现,找出其切入口,并进行攻破。
在某次练习中,有这样两道解方程组的题目:
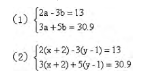
学生经过计算,得出第一个方程组的解为a=8.3,b=1.2,在解第二个方程组时,不少学生先进行去括号处理,把方程组整理成。
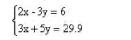
然后再用代入法或加减消元法求出方程组的解。这样做当然不失为一种方法,但也有学生做此题时联系到刚做的第(1)题,经对比后发现这两个方程组存在着太多的“形似”之处,于是根据第一题的启发,直接得到
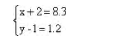
故x=6.3,y=2.2。教师应该大力鼓励和支持这些学生的创造性想法,他们善于进行观察,在对照比较中发现了解决问题的好方法。思维不落俗套,方法方便快捷。
(三)创新教学方法,培养学生的创造性思维
在传统的数学教学活动中,教师只注重把教学内容讲得清楚、明白透彻,在这种教学方法下,学生只明白了一个公式或定理,明白了一道题。为了培养学生的创造性思维,必须在教学方式上有所创新。
例如,“圆的内接四边形”教学中,在探索性质时,教师可以设计以下问题。(1)前面我们已学习了一类特殊四边形———平行四边形、矩形、菱形、正方形、等腰梯形的性质,那么要探讨圆内接四边形的性质,一般要从哪几方面入手?(2)改变圆的半径大小,这些变量有无变化?(3)移动四边形的一个顶点,这些变量有无变化?由(4)观察得出的某些关系有无变化?移动四边形的四个顶点呢?移动三个顶点呢?(5)如何用命题的形式表述由刚才的实验得出来的结论呢?
这样让学生动手的方式,使学生自己去发现结论,并用命题形式表述结论。这种“发现学习”的数学教学方式既培养了学生动手实践能力、观察能力和自学能力,也学生充分感受到发现问题和解决问题带来的愉悦,从而培养学生的数学创造性思维。
(四)允许并鼓励学生突破常规进行思考
在传统的课堂上,教师把自己的理解作为权威的教学内容向学生灌输,而学生只能无条件地接受教师的思维形式。久而久之,学生的创造性与主动性便会慢慢消弭,创造性思维被严重束缚。因此,教师在教学活动中,要时刻警惕自己成为知识的独裁者,允许、鼓励学生突破常规,甚至“出格”进行思考。虽然“出格”并不意味着创新,但是连“出格”的机会都没有,学生定然不敢逾越常规了。所以,教师要培养学生的创新思维,就必须在教学活动中发扬民主精神,提倡学生大胆的进行思考。
例如,在进行“二元一次方程组”的教学中,有这样的例题:一个笼子有鸡和兔,共10个头、28只脚,问鸡和兔各有多少只。这样一道平淡无奇的“鸡兔同笼”应用题,绝大多数学生都能通过列二元一次方程组得出正确答案。这时,我问大家“有没有更简便的方法。”大家经过思考都说没有。我启发大家,如果所有的兔子起立呢?大家一想,鸡、兔共有10个头,当所有的兔子两只脚落地,两只脚离地后,地上就有20只脚,原来地上28只脚,现在剩下20只脚,那么有8只脚起立,这样肯定是4只兔、6只鸡。大家都觉得很有趣。这时,一位同学想出了一个更“怪”的方法:假如鸡有4只脚,那么,地上有40只脚。那么多出的12只脚是鸡“生”出来的,于是算出鸡有6只,兔有4只,我大力肯定这位学生的创造性思维。全体学生也体会到创造性思维的乐趣。
总之,不管采用什么方法去发展学生的创造性思维,教师都应作为学生思维的引导者,引导他们明确思维方向和依据,更为重要的是改变教师的教学方式和学生的学习方式,为学生构建开放的学习环境,提供多渠道获取知识,并将学到的知识综合应用到实践中,切实培养学生的创造性思维。
参考文献:
[1]陈安龙.创造性思维与教学[M].中国轻工业出版社,1999.
[2]张志勇.关于实施创新教育的几个问题[J].教育研究,2000(3).
[3]刘仕森.数学课堂教学中的创新教育[J].中学数学研究,2002(1).





