数学思想是指人们对数学理论和内容的本质的认识,是数学科学发生、发展的根本.数学思想蕴涵在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括而成的数学观点.数学方法是数学思想的具体表现形式,是数学思想的具体化、程序化,具有更多的操作属性.数学思想是指向个体内部的观念,而数学方法是指向个体外部的操作.个体的数学思想需要通过具体操作方法才能体现出来.因此,在数学教学实践中,人们往往把数学思想和数学方法统称为数学思想方法而不加区别.
数学思想方法是思考数学问题和从数学角度思考问题的思想和方法,是长期的数学发展所积累的文化灵魂.如果说数学知识是关于"是什么(what)"的问题,那么数学思想方法是关于"做什么(what to do)"、"怎么做(how to do)"和"为什么这么做(why do it such )"的问题.
1 数学史的启示--数学思想方法的形成和发展规律
数学是伴随着人类社会的发展而发展起来的科学,也是人类文化的重要组成部分.数学从哲学中派生出来,成为最具有方法论价值的基础性工具性学科.迄今为止,数学已经发展成内容丰富,分支繁多,思想方法浩瀚的学科体系,其创造的知识和方法越来越广泛地应用于生产生活实践及其它学科中.一门学科能否建立起相应的数学模型,并用数学的方法进行定性和定量研究,已成为评价这门学科是否成熟的标志.数学,作为历史悠久的学科,从其发展的历史中追寻其思想方法发展的规律和特点,对数学思想方法的教学,具有重要的意义,因此,从数学史中研究数学思想方法的形成和发展规律,成为数学工作者的重要工作.许多数学家对此进行了系统研究,取得了丰富的成果,如美国数学家莫里斯·克莱因(Morris Kline)所着的《古今数学思想》,(俄罗斯)A·D·亚历山大洛夫等人所着的《数学:它的内容方法和意义》,日本的米山国藏的《数学的精神、思想和方法》[1],李文林的《数学史概论》等.
1.1 数学思想方法是数学活动的实践经验的概括
数学思想方法是在数学实践活动中形成和发展的,这种实践性既包括早期直接的社会生活生产经验也包括数学研究实践经验.数学早期的发展来自生活生产实践中计数、排序、分物的活动(产生数的概念)及丈量土地和物品装饰的活动(产生图形的概念),在这些实践中逐步发展成用符号表示数,出现线和角等基本几何概念.无论是古巴比仑的用契形文字表示数及其运算,古埃及的象形文字中数的表示与计算,还是古代中国用算筹表示数及其运算,这些都是在对生活实际中的数量进行抽象的产物.古代角的概念,也是在观察人的大腿以及臂与腿之间形成角的直观形象的基础上产生的[2].由此可见,数学抽象概括的思想的萌芽是古代从生活生产实践抽象出符号化的数和形的过程中形成的.
数学活动不仅仅是生活生产实践中的数学活动,还包括研究抽象数学的实践活动,数学家不仅仅从生活生产中发现数学,而且也不断基于已有的数学对象创造新的数学对象并对这些数学对象进行研究,在数学研究的实践中贯穿特定的思想方法.古希腊在数学逻辑思想的发展起到重要的作用,从柏拉图时期起,数学关注了抽象的概念,要求根据一些公认的原理作出演绎证明[2].数学逻辑思想方法成熟的标志是亚里士多德(Aristtotle)创立逻辑学和欧几里得(Euclid)编着的《几何原本》.《几何原本》中的大部分命题及其证明不是欧几里得的独立创造,而是他对前人个别发现的系统整理,但欧几里得的杰出贡献是把这一时期的数学逻辑推理的思想系统化并提升到初步的公理化水平,把这一数学基本思想推进到新的高度.
新的数学思想方法的产生往往是社会生活生产中的数学实践和数学研究实践的共同作用.例如,经典的几何学主要研究的是光滑曲线或曲面,最初在 19 世纪末 20 世纪初出现非光滑的曲线或曲面时,那是作为非正常的特例出现的.如康托尘集、雪花曲线、Koch 曲线等,当时对这些曲线进行了一些个别的描述,研究了这些曲线的维数.直到1967 年美籍数学家 B·B·Mandelbort 在美国的《科学》杂志上发表题为《英国的海岸线有多长?》的着名论文,分形几何才逐步成为一门独立的几何学,并逐步应用到其它学科上.分形几何中对传统图形的"维数"概念的拓展,自相似、函数叠代,调和分析的思想产生既受到前人数学思想方法的影响又受到生活实践问题(诸如海岸线、云朵、人体神经、植物结构等自然精细结构问题)的驱动,形成了描述自然精细结构的"自然图形"的几何学[3].新的数学思想方法的产生,双重依赖于社会生活生产实践中的数学活动和数学的抽象研究实践活动,这两种活动统称为数学实践活动.
1.2 数学思想方法是一种文化传承和发展
数学是一门思想方法一脉相承的学科,没有哪门学科像数学那样不能割断历史.数学思想的产生和发展,既是对前人已有的数学思想方法的继承,又是在前人已有的思想方法的基础上的创新和发展.在自然科学中,有哥白尼的日心说对地心说的颠覆;在数学中,尽管有对前人观点的质疑和改造,但最后都是对前人思想的继承和发展.如果说,非欧几何是对欧几里得几何中第五公设的否定而产生的,但也是对欧几里得几何的继承和发展.在数学发展的历史中,这种继承发展的例子比比皆是.例如,欧几里得得到了两圆的面积之比等于直径的平方之比,因此可得到圆的面积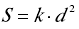
,但不知道常数 k 是多少,阿基米德(Archimedes)在此基础上得到 π 的近似值[2].欧几里得使用了穷竭法和间接证法来证明几何中的一些定理,而阿基米德则在工程实践的需要驱动下用这两种方法研究了几何图形的度量属性(如圆、椭圆、球、旋转体的面积/体积).这种度量化的思想和穷竭法是微积分思想的萌芽[4].由于古希腊人不承认无穷,就与极限失之交臂.微积分的建立,需要建立在无穷思想的基础上,需要数形结合思想(这归功于笛卡尔和费马建立的坐标法)的支撑,最终由牛顿和莱布尼茨完成,这是数学思想方法传承和创新的典型例证.此外,希腊亚历山大时期的希帕科斯(Hipparchus),梅内劳斯(Menelaus)和托勒密(Ptolemy)等人在前人用定量方法研究平面图形的基础上,为描述天体运动研究球面几何,进一步创建了全新的学科--三角学.
数学思想方法的发展,既离不开对已有思想方法的传承,更离不开对传统思想的质疑与批判.无理数的发现,是在用整数的比描述两线段之比中发现不可公度线段,从而引发了第一次数学危机,并导致了数系的扩充,促进了数学的发展.对无穷小的质疑产生了第二次数学危机,并最终驱动了微积分逻辑基础的研究,促进了数学的发展.1734 年,英国哲学家、大主教贝克莱提出了所谓贝克莱(G. Berkeley)悖论.他指出:牛顿在求x^n的导数时,采取了先给 x 以增量 d x,把二项式( x+dx)^n展开,从中减去nx 以求得增量,并除以 d x以求出x^n的增量与 x 的增量之比,然后又让 d x为零,这样得出增量的最终比.这里牛顿做了违反矛盾律的手续--先设 x 有增量,又令增量为零,也即假设 x 没有增量.他认为无穷小 d x既等于零又不等于零,召之即来,挥之即去,这是荒谬的.无穷小量究竟是不是零?无穷小及其分析是否合理?由此而引起了数学界甚至哲学界长达一个半世纪的争论.从波尔查诺(B. Bolzano)、阿贝尔(Abel)、柯西(Cauchy)、狄利克莱(Dirichlet)等人的工作开始,到魏尔斯特拉斯(Karl Weierstrass)、戴德金(Dedekind)和康托(G. Cantor)的工作结束,经历了半个多世纪,基本上解决了矛盾,为数学分析奠定了严格的基础.
对康托集合论的质疑直接引发了第三次数学危机.1897年,福尔蒂(Burali-Forti)揭示了集合论中的第一个悖论.两年后,康托发现了很相似的悖论.1902 年,罗素又发现了一个悖论,它除了涉及集合概念本身外不涉及别的概念.罗素悖论曾被以多种形式通俗化.其中最着名的是罗素于1919 年给出的,它涉及到某村理发师的困境.理发师宣布了这样一条原则:他给所有不给自己刮脸的人刮脸,并且,只给村里这样的人刮脸.当人们试图回答下列疑问时,就认识到了这种情况的悖论性质:"理发师是否给自己刮脸?"如果他不给自己刮脸,那么他按原则就该为自己刮脸;如果他给自己刮脸,那么他就不符合他的原则.承认无穷集合,承认无穷基数,就好像一切灾难都出来了,这就是第三次数学危机的实质.第三次数学危机导致了公理集合论的出现.
数学思想方法形成和发展的历史启示是:数学思想方法的形成和发展首先是建立在数学实践活动的基础上;其次,数学思想方法是对数学实践经验的概括;第三,数学思想方法的发展需要对前人思想方法的继承、批判和创新;第四,数学思想方法体系是通过不断地分化、整合、创新而不断向前发展的.
2 数学教育的需要--数学思想方法教学的基本策略
数学发展过程中形成新的思想方法的过程是漫长而曲折的,学生学习数学思想方法不可能经历数学史上的数学发现过程,而是在教师的指导下领悟前人的数学思想方法.作为教育形态的数学思想方法,既要让学生自然合理自主地产生、形成、巩固和发展,又要尽可能缩短其学习的时间进程.一方面,数学思想方法的学习需要经历数学史上数学思想的形成发展相似的阶段,即"数学实践"、"基于数学实践的理性概括"、"形成数学思想方法体系,通过分化、整合、和创新产生新的数学思想方法";另一方面,学习需要训练,因此数学思想方法的学习中要经历应用特定的数学思想方法解决问题的训练阶段.这样,可以把数学思想方法的学习过程划分为以下 4 个基本阶段:(1)操作体验(问题解决过程中数学思想方法的模仿应用和体会)阶段;(2)明朗化阶段(用明确的语言符号和图式表示数学思想方法的内涵,应用的步骤和要点);(3)自觉运用阶段(用特定的思想方法解决问题);(4)联系发展阶段(建立不同思想方法之间的相互联系,形成数学思想方法体系).
在学生学习数学的过程中,数学思想方法产生于数学活动特别是数学问题解决的实践,成熟于对数学活动实践过程的反思和总结,巩固于蕴含同一数学思想方法的问题解决训练中,发展于相互联系的过程.数学思想方法是对解决问题的基础算子(由数学概念原理得到的判断、推理和操作程序,心理学中叫做"产生式")的不断概括和组合交叉,因此数学思想方法的学习是基于数学概念原理的学习过程中的.数学思想方法可以不断抽象概括,形成不同抽象层级的数学思想方法体系.数学思想方法的学习是归纳的,是从默会到明朗化再到自动化最后到系统化的体验、感悟、巩固和深化过程,是从相对具体到相对抽象的逐步发展过程.
2.1 教学策略之一--在数学活动中渗透
数学思想方法是在数学活动过程中体现出来的信息加工的特殊方式,离开了数学活动,数学思想方法就成为脱离实际的抽象的乌托邦,不能用来提高数学信息加工的效率,不能起到发展大脑信息加工机能的作用.因此,离开具体的数学活动,数学思想方法是没有价值的.同样,在数学活动中如果没有数学思想方法的指导,数学活动就没有方向,即使获得知识,解决了问题,其知识将成为数学事实的无序堆砌,解决问题变成随机的行动,其过程变得曲折低效,而且不会对今后的问题解决形成有效的经验迁移.数学活动是针对具体的对象,伴随着知识的形成和应用过程的.在知识的形成和应用过程中渗透数学思想方法,在知识形成和应用知识解决问题后总结活动过程的认知操作程序,是引导学生体验、感悟数学思想方法的有效策略,而这种渗透,是靠教师设计适当的问题情境实现的.例如,在相交线与平行线教学中,引导学生通过观察生活中同平面内两直线不同位置关系的形象,提出研究同一平面内两直线位置关系的问题,通过画图、分类,发现同一平面内两条不同的直线要么有公共点(且最多只有一个)、要么没有公共点,从中抽象出相交线与平行线的概念.在研究相交线时,引导学生观察生活中最常见的相交线模型--剪刀及其运动,并抽象出两直线相交的动态模型,然后提出问题:怎样描述两相交直线的相对位置关系?引导学生自然合理地发现用角表示,但角有 4 个,用哪一个角表示?这就很自然地想到要研究交成的 4 个角之间的关系,从而引导学生研究邻补角和对顶角.在教学过程中,引导学生经历"化线为角"的过程和逻辑推理的过程;在获得邻补角和对顶角知识后,引导学生思考"通过怎样的步骤得到这些知识?",让学生总结出"画相交直线--形成角--用角度表示两直线位置关系--研究 4 个角关系--对顶角性质、邻补角性质--交成的 4 个角中如果一个角确定,则其余 3 个角的大小也唯一确定","画图--观察--猜想--说理".这样,学生就能对"化线为角"和"逻辑推理"的思想有初步的感悟,同时,在后面的垂线、平行线教学中继续渗透这两种数学思想方法,这两种数学思想方法的体验会得到深化.化线为角和逻辑推理的思想在高中立体几何研究线线、线面、面面关系中会继续应用和深化.
抽象概括和推理是数学思维的基本形式,也是数学的基本思想方法.其学习的过程也需要经历操作体验、明朗化、自觉运用和联系发展 4 个阶段.例如,中小学生学习抽象概括,基本上是处于操作体验阶段,模仿着在一些概念的形成过程及数学模型建立过程中进行抽象概括活动,学生既没有能力也没有必要知道数学抽象概括的内涵、操作步骤及要点.然而,有很多中学教师也没有很好地理解什么是抽象概括,造成教学过程中对抽象概括活动的忽视或扭曲.例如,在初中函数概念教学中,很多教师没有从函数概念发展的历史中领悟函数概念的发展阶段,要么把函数概念硬塞给学生,造成学生的死记硬背,要么把函数概念的抽象过程当成具体几个函数(甚至是非典型的函数)共同特征的一步到位的归纳.其实,初中变量说下的函数概念形成需要两次概括过程,第一次概括出能根据公式确定自变量与应变量之间的函数关系,让学生确信所谓对应是知道了自变量的值就可以确定出唯一的函数值(通过用公式算出让学生确信);第二次概括出函数关系不依赖于具体的表示方法(只要能由自变量的取值唯一确定函数值即可,可以用任何方式确定,不一定要通过公式计算来确定).合情推理和演绎推理是两类基本推理方式,学生学习这两种推理方式时,首先要在熟悉的知识领域内模仿着做,在会做的基础上再思考推理的含义,学习什么叫合情推理,什么叫演绎推理,推理的基本模式和基本要求,推理的具体操作步骤和方法(如演绎证明中的分析法、综合法、反证法等),各种推理在数学活动中的作用(如合情推理用于发现结论,演绎推理用来证明结论)等(如人教版高中 A 版教材中安排"推理与证明"的教学内容)[5],再通过训练学会自觉运用,综合运用各种推理方法解决问题,最终逐步形成用推理建立数学内容内在联系的思想.
方程思想是初中数学的重要思想,是数学基本思想--模型思想的下位思想方法.学习这一思想方法的过程也需要先让学生在一个学习阶段内不断根据实际问题中的数量关系列方程,通过解方程间接地获得实际问题的解,并引导学生不断地总结解决问题的步骤和方法,这样才能形成方程思想应用的深刻体验.
2.2 策略之二--在反思总结中明朗化
数学思想方法蕴含在数学活动实践中,但数学思想方法形成的关键在于对数学活动实践经验的总结和概括,也就是说,把运用于某些问题解决过程的基本思想和方法一般化、程序化、模式化.在自然状态下(没有外在干预启发的情况下),这种概括是缓慢而曲折的.例如,笛卡尔和费马发明平面直角坐标系前,古希腊的阿波罗尼奥关于圆锥曲线性质的推导、阿拉伯人通过圆锥曲线交点求解三次方程的研究,这些做法都是坐标法的萌芽.然而,坐标法的真正形成,需要把萌芽状态、针对具体问题的解决方法一般化、程序化和模式化.古希腊和阿拉伯没有进行这种实践经验的概括,直到笛卡尔、费马把坐标方法一般化,才真正创立了坐标法.同样,积分思想的萌芽产生于古希腊及古代中国等地的用"穷竭法"和"无穷小思想"求一些特殊图形的面积、体积过程中,但直到牛顿和莱布尼兹把这种方法一般化、程序化、模式化后才正式产生了积分思想.
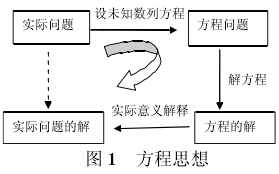
在数学学习中,数学思想方法的建立同样需要经历一般化、程序化和模式化的概括过程,没有这种概括,在具体问题解决中产生的具体方法就不能推广到一般,也不能形成有效的迁移.因此,在数学思想方法教学中,应该引导学生进行数学活动实践经验的概括,而这一概括过程是在解决问题后,通过反思、总结进行的.例如,在经历了一些根据实际问题建立方程,通过解方程间接解决实际问题后,学生具有一定的列方程解应用题的经验,这时,需要学生在解决问题后,通过解后的反思总结,得到运用方程解决实际问题的基本思想如图 1.
再如,数形结合是数学典型思想之一,学生在小学数学学习中就有接触到,比如求平行四边形和圆的周长和面积,在这种图形度量属性的研究中体现了用数量来刻画图形的属性的基本思想.在初中数学中,用数量刻画图形的属性,用图形表示数量关系的现象更多.数轴和平面直角坐标系的学习,体现了用数量关系刻画图形的位置;两直线位置关系的研究,采用了化线为角,用角度大小刻画两直线位置关系的思想;长度、距离、面积的研究,体现了用数量表示图形的度量属性的思想;相似(全等)三角形的研究,体现了用长度和角度刻画图形形状关系的思想;函数图象则是用图形刻画数量依存关系的典型模型,体现了以形助数和以数助形的基本思想,前者是把抽象关系直观化,后者是用数量关系进行精确、可靠的研究.这些内容教学中,应该引导学生在体验的基础上总结出数形结合的思想.先实践体验,再反思总结,把具体做法一般化、程序化和模式化是进行数学思想方法提炼的关键认知操作.
2.3 策略之三--在运用训练中巩固
数学思想方法是一种数学实践经验,产生于数学活动的实践,运用于数学活动实践.数学思想方法是具体问题解决方法的一般化,这种一般化的过程是一种归纳的过程.例如,在研究相交线时采用了用角度大小研究两直线相对位置关系--相对倾斜度,在垂线学习和平行线研究中继续运用了这种方法,于是就可以把用角度表示两直线相对位置关系一般化到研究平面上任意两条直线的位置关系乃至空间两直线的位置关系(异面直线的交角).在牛顿和莱布尼兹之前,无穷小量分析方法已经零散地出现在具体问题的解决中,在古希腊时期,欧几里得、阿基米德等人及在古代中国都有用这种方法求一些特殊图形的面积体积,这可以说是积分方法产生的萌芽;德国数学家开普勒(Johannes Kepler)在研究圆锥曲线旋转而成的旋转体体积时用到无穷小分析法;意大利数学家卡瓦列里(Bonaventura Cavalieri)利用无穷小量(他说是"不可分量")原理建立了等价于下面积分的基本结果,使积分思想实现了一定范围内的一般化：
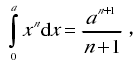
直到牛顿莱布尼兹正式承认无穷小量并把这种方法一般化到算法水平,并建立了微分与积分的联系,微积分的思想才正式创立并广泛地得到应用[4].数学思想方法形成的归纳过程,需要充分的样例积累.用相同的思想方法解决不同形式、不同领域问题的过程经历,是提高归纳的信度,把思想方法一般化、程序化和模式化的基础,也是促进学生把数学思想方法应用到新的情境,产生远迁移的重要因素.例如,在一元一次方程学习中,学生经历了方程思想的体验、明朗化阶段,但要使方程思想内化成学生大脑内的一种自动激活操作,在各种情境下能自如运用方程思想,则需要在一元一次方程、二元一次方程组、分式方程、一元二次方程等内容的学习中进一步进行用方程思想解决问题训练,在各种问题的方程建模实践中巩固方程思想,使学生能有意识地运用方程思想建立问题中数量之间的联系并通过解方程间接地获得问题的解.
2.4 策略之四--在相互联系中发展
作为数学学科的核心和精髓,数学思想方法具有系统性.经长期的发展,数学已经形成典型的、独特的、丰富的思想体系.数学思想方法的系统性主要体现在以下几方面:
(1)数学思想方法具有层次性.作为问题解决路径中基础算法的一般化和模式化,数学思想方法的发展是从特殊到一般、从具体到抽象的过程.从针对具体问题的特殊方法到针对一类问题的方法再到抽象的思想和观念的发展过程.数学思想方法的不断概括抽象过程如图 2.
例如,通过具体的列方程解决实际问题的经验的抽象,获得方程思想;通过列不等式解决实际问题获得不等式模型思想;通过建立函数模型解决实际问题得到函数思想;利用统计模型解决实际问题概括出统计思想;在这些思想方法的基础上,通过再次一般化、程序化和模式化,概括出数学模型思想如图 3.
进一步,还可得到数学关系映射和反演思想(如图 4):
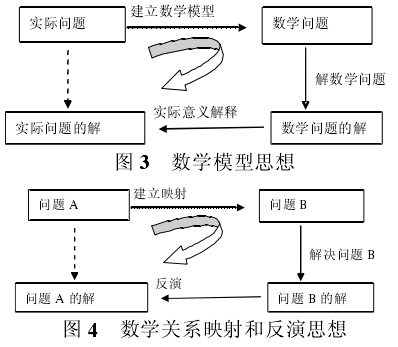
再进一步一般化和模式化,可以抽象到数学化归与转化思想.
(2)数学思想方法具有横向联系性.数学思想方法除了具有纵向抽象的层次性外,还具有横向的联系性.通过思想方法的类比、交叉、融合,可以派生出新的思想方法.以这种派生出的思想方法系列为典型样例,又可以概括出包颞性更广的新的思想方法.例如,类比方程思想可以得到函数思想,而方程思想和函数思想是形成数学模型思想的典型样例和归纳基础.数形结合思想可以把数的问题转化为形的问题,也可以把形的问题转化成数的问题;消元思想则是通过消元减少未知数个数把多元方程组变成熟悉的方程组;模型思想则是通过建立适当的数学模型把问题转化成熟悉的模型,用模型建立已知与未知之间的联系,从这种联系中规划解决问题的思路.这些思想方法都是数学化归与转化思想的典型样例,是形成"化未知为已知、化随机为确定、化复杂为简单、化陌生为熟悉、化隐晦为明朗、化无序为有序"这种化归与转化思想的归纳基础.数学史上,数学思想方法的分化、融合和交叉是不断进行的,从统一走向分化,产生许多数学思想方法的分支,再在分化的基础上走向融合,最后又重新分化,这种融合--分化的循环往复不断地推进着数学的发展.例如,古希腊欧几里得时期,是把先前的基于社会生活实践的数学思想统一到初步的公理化逻辑思想上;然后是把这种逻辑思想应用到各领域,产生数学思想方法的分化;笛卡尔通过创建坐标法,把代数研究方法和几何研究方法相融合,形成了数形结合思想;20 世纪初,布尔巴基学派又把各种数学内容基于集合论和模式化统一融合成代数结构、序结构和拓扑结构;20 世纪中后期,数学思想方法一方面不断分化,形成各种新的数学分支和新的思想方法,另一方面,数学思想方法又走向大融合、大交叉.初步形成了数学抽象概括、数学推理、数学模型、数量化精确化、程序化算法化机械化等思想,其中,数学抽象概括的思想、推理的思想、模型的思想是最基本的思想.通过抽象,把外部世界与数学有关的东西抽象到数学内部,形成数学研究的对象;通过推理,得到数学的命题和计算方法,促进数学内部的发展;通过模型,创造出具有表现力的数学语言,构建了数学与外部世界的桥梁[6].
(3)数学思想方法具有发展性.数学的发展伴随着新的思想方法的产生和发展,数学的发展也依赖于数学思想方法的创新和发展,没有新思想方法的不断产生,就不会产生有价值的数学知识.不论是基于无穷小分析的微积分的产生发展,基于微分分析和级数收敛分析的调和分析的产生,基于微分方程的动力系统的产生,还是数学机械化思想的产生,都是现代数学伴随着思想方法的创新而发展的过程.学生大脑中的数学思想方法,也是从具体到一般,从直观到抽象,从局部到整体地发展的.这种数学思想方法的个体发展性,要求在数学教学中遵循数学思想方法教学的从体验感悟到明朗化自动化、从特殊到一般,从局部到整体,从具体方法到数学思想的循序渐进原则和及时反思总结、相互联系的自组织和系统化原则.
钟志华,宁连华,白会平等认为,搞好数学思想方法教学的关键在于牢固把握核心观念并以此基础构建数学思想方法网络[7],核心观念应该指的是基本数学思想(抽象的思想、推理的思想和模型的思想),数学思想方法网络则是通过横向联系和纵向概括活动来逐步构建的.在教学实践中,既要在平时教学中不断渗透数学抽象、推理、模型这些最基本的数学思想,又要让学生不断地进行数学思想方法从具体到抽象、从简单到复杂的明朗化总结和应用训练,还要在相互联系中发展自身的数学思想方法体系.要建立这种数学思想方法体系,需要在学生巩固已有的数学思想方法的基础上,通过不同思想方法及其应用过程的比较,建立不同思想方法的横向联系,并进行综合应用(如组合几种数学思想方法,把一种数学思想方法嵌入到另一种数学思想方法之中,类比一种数学思想方法产生新的数学思想方法等),再把这种横向相互联系的数学思想方法作为基础思想方法,并进一步概括其共性,形成上一抽象层次的数学思想方法.通过这种横向比较拓展和纵向抽象概括,不断扩展和优化已有的思想方法网络.例如,在相交线和平行线中让学生感悟和巩固化线为角的数量化思想方法,在四边形学习中感悟化四边形为三角形的思想方法,在几何探究中学习特殊化和一般化、几何变换和分类讨论思想方法,在代数教学中让学生把握消元转化、方程、函数等模型思想方法,在此基础上通过比较和抽象,形成数学化归与转化思想.这样,学生头脑中的数学化归与转化思想是具体的,是有丰富的内容的,比如,数形转化,特殊与一般的转化、动静转化、部分与整体的转化、条件和结论的转化、模型结构交叉、分拆、组合的转化、正反转化等,这对形成数学转化思想的深刻感悟,形成成体系的数学思想方法,无疑是非常重要的.
[参 考 文 献]
[1] 燕学敏,华国栋.国内外关于现代数学思想方法的研究综述与启示[J].数学教育学报,2008,17(3):84-87.
[2] M·克莱因.古今数学思想[M].张理京,张锦炎,江泽涵译.上海:上海科学技术出版社,2002.
[3] Kenneth Falconer.分形几何[M].曾文曲译.北京:人民邮电出版社,2007.
[4] 李文林.数学史概论[M].北京:高等教育出版社,2003.
[5] 普通高中课程标准实验教科书 A 版·数学·选修 1-2[M].北京:人民教育出版社,2007.
[6] 史宁中.漫谈数学的基本思想[J].数学教育学报,2011,20(4):8.
[7] 钟志华,宁连华,白会平.例谈数学思想方法的教学策略[J].数学教育学报,2007,16(3):13-16.
