
随着课程改革的不断深入,传统的教学观念在数学教学中也有所转变,为突出理论结合实践,侧重培养学生数学应用意识,教材的编写也结合了许多实际活动和社会热门问题。针对教学改革,在中学数学中引入数学建模思想想必也会有非凡的效果。数学建模与最常用、有效的教学方法即探索法有很多共同特征。因此本文通过数学模型、数学建模思想,探讨数学建模思想应用于中学数学教学的可行性,为中学数学课堂教学改革寻找一条可行之路。
一、数学建模及数学建模的基本理念
所谓数学模型,是指针对或参照某种事物的特征或数量相依关系,采用形式化的数学语言,概括地或近似地表述出来一种数学结构。广义的解释:凡是一切数学概念、理论体系、各种公式、方程(函数方程、微分方程……)以及由公式系列构成的算法系统等都称为数学模型。而创建一个数学模型的全过程称为数学建模,即用数学语言、方法去近似地刻画该实际问题,并加以解决的全过程。
总之,数学模型与数学建模较为严格的定义是对于现实世界的一个特定对象,为了一个特定目的,根据对象特有的内在规律,在做出问题分析和一些必要、合理的简化假设后,运用适当的数学工具,得到的一个数学结构就称为该特定对象的数学模型。数学建模的过程,可用如下框图来说明:【图】
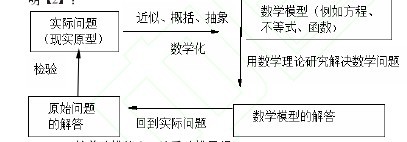
二、培养建模能力,注重建模思想
(一)从教材原题的改变出发,注重建模思想的引入在中学数学中,我们常发现一些应用题是通过改变设问方式,变换条件等拓广类比成新的问题,这一点极其地展现了建模思想在教材原题改变中所发挥的作用。编者们依照科学性、现实性、可行性、新颖性及趣味性等原则,在一些原有应用问题的基础上编拟出有实际背景或有应用价值的建模应用题。
【例题1】:一个长为5米的竹竿靠在墙上(如图1所示),竹竿顶端距地面的垂直距离4米,如果竹竿的顶端下滑1米,那么(1)底端也将滑动1米吗?
(2)列出底端滑动距离所满足的方程。
(3)求出方程的近似解?底端滑动的距离比1米大还是小?
该题是由北师大版《数学》八年级下册第17页B组第一题改变,类似题在其它版本教材及练习册上也多次出现。我们细心挖掘,课本中都有可以挖掘出的生活模型,因此建模思想也就自然而然地融入其中了。在教学过程中可以选择紧贴实际生活的典型问题深入分析,逐渐渗透建模思想,使学生养成自觉地把数学作为工具来解决问题的意识。这样的教学模式能够培养学生的应用意识和能力。
(二)从课堂教学出发,注重建模思想的引入
在中学数学教学中,针对不同的教学内容引入不同的数学模型进行教学,既可以激发学生对数学这一学科的兴趣,又可以增强学生的应用意识、培养学生应用数学知识和计算机技术解决实际问题的能力。例如讲解数列的概念,可以通过引入存钱例子(储蓄模型)进行讲解,使学生更好地理解掌握。
【例题2】:一对夫妇为给他们的独生子女支付将来的大学学费,从孩子一出生每年都到银行储蓄一笔钱。设大学学费每年需4000元,四年共需16000元,银行储蓄年利率为11%。按复利计算,为使孩子到18周岁上大学时本利和共16000元,他们每年需存多少钱?(精确到元)解:设每年需存x元则x{(1+0.1118)+(1+0.1117)(1+0.1116)+……+(1+0.11)}=16000∴1.11x(1.1118-1)/(1.11-1)=16000x(1.1119-1.11)=1760x=1760/(1.1119-1.11)≈288(元)
(三)从学习方法出发,注重建模思想的引入
在学习过程中,学生难免会遇到不懂的知识,这时老师的工作就是选择恰当的方法为学生讲解,引用建模思想进行教学一定会有效果。这有助于学生全力把目前所学的知识弄懂,并进一步把知识应用到实际生活中。
让学生们真正明白知识应用于生活、生活源于知识的道理。否则,一些学生认为学习知识就是为了考试和拿毕业证。
(四)从课后作业出发,注重建模思想的引入
1、在作业格式上:
在课后作业中,很多学生可以想出类似模型、找到求解方法,但却不知如何表达出来,很难让别人看懂;此外还有部分学生不注意作业的格式,认为有结果就行。实际上,平时的作业和我们的表达能力以及科学写作能力都是息息相关的。因为数学建模论文要求用语宜凝练醒目、精确、要通俗易懂、思路清晰,所以在平时的作业中将建模思想贯穿于其中,有利于培养学生的表达能力、逻辑能力等。
2、在作业内容上:
教材里设置的习题,一般是一些条件充分,答案确定的问题,这不利于培养学生的创新能力。因此在布置作业时要与其他学科相联系、从实际生活中出发。这样可以给学生更大的思维空间、积极引导学生进行探索,使学生感受到数学应用之所在,通过作业来体验教学、认识教学、掌握数学建模的思想方法。
中学数学教学引入建模思想,目的是要促进学生更好地学习和掌握数学的基本知识,提高学生的数学应用意识和创新能力。在实施教育过程中应当正确处理好教学的“严谨性”和“实用性”之间的关系,促进教学改革的发展。
参考文献:
[1]沈新权.构建建模意识培养创新新思维[J].中学数学教育,2009.
[2]徐兆棣,李晓毅.数学建模[M].沈阳:辽宁大学出版社,2006.
[3]李华彬,陈勇.《数学》八年级下册[M]北京:北京师范大学版,2006.
[4]刘来福,曾文艺.问题解决的数学模型方法[M].北京:北京师范大学出版社,1999.





