
学习并不是单纯地模仿和记忆,不是被动地吸收、反复地练习和强化记忆,而是学生以已有的知识、经验为基础,通过主体与客体的相互作用主动去建构意义的过程.教师切忌直接把知识强塞给学生,而要通过创设一定的情景,引导学生经历观察、实验、猜想、验证、推理等数学活动,从而使学生理解数学知识并形成自主的学习经验.
学习中对同一个问题从不同角度、不同方向依据题目所提供的条件,借助一些思想方法的指导,从而挖掘出尽可能多的有用信息,设想出多种解决问题的方案,并利用已有知识分别解决问题的过程,我们称之为一题多解.在一题多解的问题情境下,学生的思维活动逐渐在问题信息的激发下活跃起来,各种新颖的见解逐一产生,解决问题的思路逐步在学生的主动思考或同学间的相互交流、合作下形成并不断得到完善.学生通过一题多解,使知识本身被掌握和应用,加强了各知识点之间的有效整合,形成了对知识体系的重新建构,同时开拓了思维,锻炼了解决问题的灵活性,提炼了解决问题的思想方法,获得了一定的知识和经验.
因此,作为一线教师,我们对一题多解应给以足够的重视,要看到它在数学课堂教学中的有益之处,以便更好地利用其提高课堂实效,促进教学质量的提高,使学生在获得知识的同时,思维和技能得到提升.以下我将结合具体实例从四个方面谈谈对数学课堂教学中的一题多解的浅显认识.
一、一题多解能调动学生的学习兴趣和热情,活跃课堂氛围,有利于培养学生的发散性思维
培养发散思维就是要使学生灵活应用所学知识从不同角度去观察问题、解决问题.学生要能够通过自己的观察、分析、推理、综合得出结论,从不同途径,用不同形式去解决问题,这是发展创造性思维的基础.有了发散性思维,学生就能发现新知识、新规律,形成新的知识体系和知识结构.
现代数学教育理论认为,数学教学是数学活动的教学,解题活动是数学活动的主导部分,而解题活动的实质是思维活动(也就是分析、解决问题的过程).因此,在数学教学中以解决问题为中心设置一些能培养学生发散性思维的题目,既有利于学生理解数学知识、掌握数学思维方法,也能锻炼学生的数学思维能力,促进数学知识与技能的全面和谐发展.
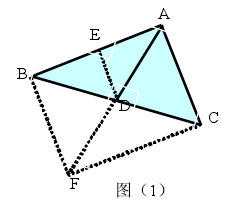
例1:如图(1),在△ABC中,AD是BC边上的中线.AB=8,AC=6.求AD的取值范围.
分析:
解 法 一 : 如 图 , 延 长 A D 至 F , 使DF=AD,连接BF、CF,
则四边形ABFC是平行四边形,
所以,BF=AC=6.
在△ABF中,由三角形任意一边大于其他两边之差,而小于两边之和,得AB-BF<AF<AB+BF

解法二:作AB的中点E,连接DE,则DE是△ABC的中位线,
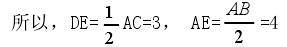
在△AED中,由三角形任意一边大于其他两边之差,而小于两边之和,得AE-BD<AD<AE+BD,所以,1<AD<7.
一题多解的问题是调动学生积极参与思维活动的一种有效途径,它给学生足够的机会、更多的思考方向,有利于发散性思维和创造性思维的培养和发展.
二、一题多解发挥了学生的主体作用,使得每个学生都参与到数学学习中去,有利于因材施教
在教学中,我们面对的学生基础不同,性格各异,兴趣爱好有别,无论是学习较好的学生,还是基础较差的学生,存在多方面的差异.教师要看到差异存在的必然性和客观性,在教学中采取必要措施去照顾学生的个体差异,因材施教,使每个学生都能参与到学习中,主动思维,最终获得不同程度的发展.一题多解的题目具有思路广、方法多的特点,适合不同层次的学生共同学习、探究.在这个学习过程中,每个学生都能参与其中,积极思考,发表意见,使原有的知识和方法在不同程度和范围得到了应用和更新,使经验得到积累,智力水平得到不断提升.
一题多解的教学过程正可谓是仁者见仁、智者见智的学习过程,但要强调的是,在这个过程中,无论学生的见解常规老套,还是新颖独到、别具一格,都应得到教师及时有效的鼓励,以激发学生的学习热情和创造灵感,打开思维空间,使不同层次的学生各有所思、各有所想、各有所为、各有所得.
三、一题多解能加深学生对已有知识和方法的理解和掌握,使学生体会各知识点间的相互联系,使学生的知识体系再次重构,形成新的认知体系
联系是指一切事物、现象、过程之间及其内部诸因素之间的相互影响、相互作用和相互制约的关系.数学知识、数学思想方法、技能是一个相互联系的有机体.知识和思想方法之间是内容和形式的关系,数学知识是基础.没有知识,思想方法就是无源之水、无本之木;而没有思想方法,知识就是一盘散沙.正如有人所说的,数学知识是一堆零件,思想方法则是一张图纸,而把零件组装成机器的是技能.
新课程标准指出,学生掌握数学知识,不能依靠死记硬背,而应以理解为基础,并在应用中不断巩固和强化.这也就是说,知识应该在理解-应用-理解的不断循环中掌握.在一题多解的学习中,学生为了达到解决问题的目的,使原有的知识和方法在不同思维的支配下被有效应用,既加深了对知识、方法的深层次理解和认识,也使原有知识得到了更新,思想方法得到了拓展.
四、一题多解能够形成有效的评价
一题多解后,学生要对各种不同的方法进行评价,比较它们在解题中的繁简、优劣,总结、归纳出各种思维方法的适用条件和范围,形成自己的经验技能.同时,通过一题多解学生还能达到对试题本身的深层次认识和评价.同时,一题多解还可以为教师在教学设计时的实体选择和设计提供参考和帮助.

方法二:设Rt△ABC的一条直角边为x,则另一条直角边为30-x.在Rt△ABC中,由勾股定理得:x²+(30-x)²=20²,即x²-30x+250=0,由一元二次方程根的判别式△=b²-4ac=30²-4×250=-100<0得此方程无解,也就是说这样的直角三角形不存在.
上述问题若只为得到结果,学生只需掌握方法一足以,但若能从方法二的角度再次认识问题,我们却发现,这样的三角形根本就画不出来,自然,它的面积还可能是125m²吗?这样的题目虽能练习完全平方公式的应用,但它反映的事实与现实不符,所以,要对题目加以修改,使其符合事实.
教学中,教师要积极主动地预设一些有利于教学的一题多解型题目,让问题的解决方式以开放的形式出现,要充分尊重学生的能力,给学生一定的时间,调动他们的积极性,鼓励他们根据自己的知识、经验、理解进行思维,畅所欲言,发表自己独特的见解.同时,作为教师,也应细心发现每位学生的"亮点",营造出一种互动、和谐、有效的数学课堂教学氛围,使学生在共同探索、相互学习中发展思维,学习数学.
参考文献:
[1]张俭福.数学教学中一题多解的调控机制[J].数学通报,2007(11).
[2]李文斌.从初中数学的一题多解谈培养中学生创新思维能力[J].中国校外教育,2010(7).





