
一、初中生几何图形学习的现状及分析
《义务教育数学新课程标准(2011 版 )》中指出 :初中阶段的学生应该具备一定的空间想象能力和基本的作图技能, 能借助于图形有利于描述和分析问题,通过形象的图形,同时采用数形结合的策略,把复杂的数学问题变得简洁明了.
但是在我们的实际教学中发现,当一个图形中线条纵横交错,局部图形重叠遮盖,学生观察图形时有很大的困难,难以识别、选取基本图形,很多学生遇到复杂的图形或图形的变化就束手无策,甚至于一见到这种类型的题目就害怕. 在课堂教学中没有留出足够的时间让学生养成观察图形、分析图形、运用图形的好习惯,使得学生普遍缺乏几何形象的空间想象能力以及运用几何图形解决问题的能力. 因此,分析造成这种现状的原因,进而突破困难显得尤为迫切.
二、初中生几何图形学习困难突破的对策
1.让学生动手剪一剪 、拼一拼 、画一画 ,对图形产生形象直观的了解数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上. 在几何图形教学中, 以学生最熟悉的三角板等道具,辅之以运动变换等手段进行研究,能激发学生探求数学奥秘的欲望,学会研究问题的方法.
1.1 擅于利用三角板、圆规等工具解决问题. 例如下面的图形是解直角三角形中的基本图形, 在解直角三角形的应用问题中都可以抽象出这些图形. 我们可以让学生动手用两块三角板拼出这样的图形,找到两个直角三角形之间的联系,即有一条公共的直角边. 再利用锐角三角函数值求解,用这样的方法可以解决这一类问题.

1.2 从学生的实际生活体验中加深对图形的转化和认识. 数学课程应在重视将现实世界中的有关空间与图形的问题作为学习的素材,使学生从生活的空间中"发现"这些图形,经历现实中抽象出数学模型的过程,体验图形与现实世界的密切联系.
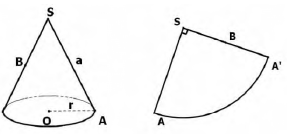
如在讲圆锥的侧面展开图时, 可以让学生把事先准备好的圆锥的模型剪开,得到扇形,再把侧面展开图恢复成立体图形,来寻找立体图形和它的侧面展开图之间的联系,从而推导出计算公式.
这样在求圆锥表面最短路程的问题时学生就容易联想到侧面展开这个方法.
2.重视题意的分析 ,把握题目的弦外之音 ,引导学生正确地画出图形
在教学中我们发现有些学生非常畏惧几何题目, 觉得无从下手. 尤其是在没有图形或图形变化后要自己画图的情况下,常常不知道怎么作图或作错图,导致错误的答案. 分析原因,主要是学生对题目本身的意思不理解或存在偏差. 因此,分析题意,作出正确反映题意的图形,是解决几何问题的第一步.
3.抓住图形特征,挖掘图形中的隐含条件
所谓隐含条件是指题目中含而未露、不易察觉的固有条件(包括几何意义及数学模型).这些条件常巧妙地隐藏在题设的背后,极易被人们所忽视. 解题时,常因未能发掘题中的隐含条件,使求解陷入困境. 若能深入发掘题目中的隐含条件,并充分加以利用,常常可以使问题得到迅速而巧妙的解决.
例如, 图形中若有平行线和角平分线必定能转化出等腰三角形. 如图,将一宽为 1dm 的矩形纸条沿 BC 折叠,若∠CAB=30°,则折叠后重叠部分的面积为 _____dm².
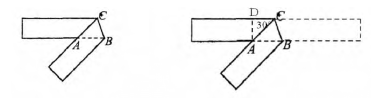
分析:由题目中的条件学生只能求出 AC 的长为 2,由于忽略了图形是折叠得到的,没有发现这里有平行线和等角,就不能发现隐含条件△ABC 是等腰三角形,可能就做不出来了.
又如在图形中若有中垂线, 通常要想到用中垂线的性质构造等腰三角形.
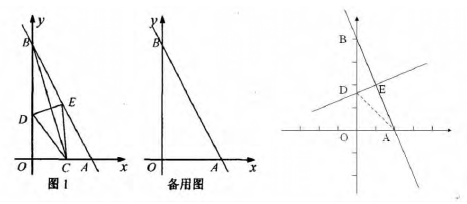
如图 1,已知直线 y=-2x+4 与两坐标轴分别交于点 A、B,点 C为线段 OA 上一动点,连结 BC,作 BC 的中垂线分别交 OB、AB 交于点 D、E_____.
(l)当点 C 与点 O 重合时,DE=_____;
(2)当 CE∥OB 时,证明此时四边形 BDCE 为菱形;
(3)在点 C 的运动过程中,直接写出 OD 的取值范围.
因此,有些数学问题其部分条件隐于图形之中,若能抓住图形"特征 ",应用运动变换的观点 ,恰当地添设辅助图形 ,就能发现含而未露的条件,使问题获得解决. 老师在上课时要把相关问题的典型例题讲清、讲透,或让学生通过题目总结得失,这样才能提高学生的图形分析能力和解题能力.
4.化繁为简 ,教会学生分解复杂图形为多个简单图形
图形的变换或者动点类题型具有运动、开放等特点,对学生具有挑战性,在中考中常以压轴题的形式出现. 由于这类题型综合代数中的函数、方程、不等式,几何中的三角形、四边形、圆、三角函数等相关知识,考察学生的动手能力、想象能力、阅读审题能力,所以通常难度都很大. 大部分学生一看到复杂的图形就无从下手了,或者不能准确画出变化后的图形,导致失分严重. 要解决这个难题,首先在理解题意后要学会将复杂的图形进行分解, 在不同的条件下准确画出需要的图形,把暂时不必要的条件忽略,这样图形简单清晰,便于学生从中找出需要的结论.
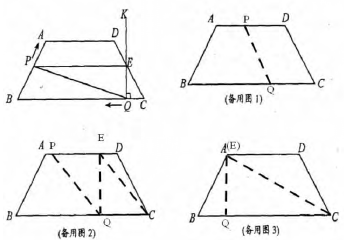
例如如图,在等腰梯形 ABCD 中,AD//BC,AB=DC=50,AD=75,BC=135, 点 P 从点 B 出发沿折线段 BA-AD-DC 以每秒 5 个 单位长的速度向点 C 匀速运动; 点 Q 从点 C 出发沿线段 CB 方向以每秒 3 个单位长的速度匀速运动,过点 Q 向上作射线 QK⊥BC,交折线段 CD-DA-AB 于点 E,点 P、Q 同时开始运动,当点 P 与点 C 重合时停止运动,点 Q 也随之停止. 设点 P、Q 运动的时间是 t 秒(t>0).
(1)当点 P 到达终点 C 时,求 t 的值,并指出此时 BQ 的长;
(2)当点 P 运动到 AD 上时,t 为何值能使 PQ//DC?
(3)t 为何值时,四点 P、Q、C、E 成为一个平行四边形的顶点?
(4)△PQE 能为直角三角形时 t 的取值范围 _____.
分析:本题是典型的动点问题,题目只给出了一张图,但在不同的小题中,动点 P、Q 的位置是不断变化的,这就需要学生根据需要画出对应的三张图(如备用图 123),化繁为简,简洁明了,便于学生解题.
在平时的教学中, 对这类图形变化问题或动点问题要分专题来讲,要耐心细致地教学生一步步分解图形,让学生养成分解图形的习惯,逐步培养他们的画图能力和转化能力. 应当不失时机的渗透各种数学思想:化归思想、函数思想、转化思想、分类讨论思想等等,可为突破"动态数学"起到关键作用.
总之,在教学过程中应多创造一些让学生识图、作图的机会,让学生仔细分析题意,识别图形,经历作图的每一步,亲身经历知识的形成过程,进而不断增强学生的作图意识和识图能力,使存在学生外部的几何知识内化到学生自身的知识结构中, 有效的促进几何学习潜能的发展.
参考文献:
[1]马复,凌晓牧.新版课程标准解析与教学指导(初中数学),北京大学出版社,2012.7
[2]初中数学画图解题能力的培养初探[J]教育教学论坛,2010,(17)
[3]王志渊.动态几何问题的信息分析与策略运用[J]中小学数学:初中版(京),2011(1/2):55-58
[4]浦静滢.合理运用现代技术,不断提高教学效能[J]数学通报,2011,50(4)





