三、数学复习课作业设计的形式与方法
(一)知识性作业的设计
1.按知识结构设计作业层次。一般可以有三类,A级为基本练习:重在基础知识和基本技能的操练,浅显易懂,紧扣当天所学的内容;B级为提高练习:重在对知识的理解和运用,难易尺度是学生“跳一跳,够得着”;C级即创新练习:重在对概念的深刻理解和灵活运用,这种题目有一定的难度。
案例四:如在复习一次函数的概念后,可以设计这样一份作业:
一、填空题
(A)(1)已知函数y=(m+1)x+2m-4当m_______时,它是一次函数;当m______时,它是正比例函数。
(B)(2)若一次函数y=2m(x+1)-4表示正比例函数,则m=_____.
(B)(3)已知函数y=(m-3)x+m+1是关于x的一次函数,则m=___.
二、解答题
(B)(4)已知函数y=(k²-4)x-k
①当k为何值时,这个函数为正比例函数?并求解析式;
②当k在什么范围内取值时,这个函数是一次函数?
三、探究题
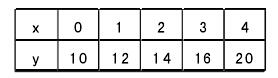
(C)(5)观察表中,y与x是否成一次函数关系?如果是,求该一次函数的解析式,如果不是,改动尽量少的数字,使其成为一次函数,并写出解析式。
(C)(6)已知2y-2m与3x+4n成正比例,证明:y是x的一次函数。这样,通过基本的、提高的、创新的不同层级的题组作业,不同程度的学生能够对一次函数以及正比例函数的概念得到最大程度的理解和掌握,并在实际问题中灵活运用。
2.同一类问题设计有梯度
对有一些题由易到难的设置问题,使学生踏着阶梯一步一步探索,让每一位学生都能获得不同程度的成功尝试,激发学生的潜能。从教学效果的角度看,设问的多梯度性可以帮助学生发掘问题的各个方面,达到深层次认识问题的本质,有利于培养学生的纵向思维。
案例五:在复习等腰三角形时,设计如下作业:
(1)如果等腰三角形的一个底角为70度,那么它的顶角是多少度?
(2)如果等腰三角形的一个为顶角70度,那么它的底角各是多少度?
(3)如果等腰三角形的一个内角为70度,那么它的其余的角各是多少度?
(4)如果等腰三角形的一个内角为100度,那么它的其余的角各是多少度?
(5)如果等腰三角形的一个内角为n度,那么它的其余的角各是多少度?
这样,通过以上由易到难的题组作业,学生按照有顺序的、可预测的方向进行纵向思考,在逐步体验数学成功的喜悦的同时,加深了对问题的本质理解。
3.根据易错题设计矫正型作业
通过精心设计典型的作业易错题,及时渗透所学的数学思想方法,能使学生掌握知识的学习任务所需的时间大为减少,学习的达成度就越高。笔者曾经在2010年编写了校本课程二次函数矫正型作业设计,以下是部分内容:
案例六:基于性质的《二次函数》矫正型作业例1:已知函数y=3x²-4x+1,当0≤x≤4时,求y的变化范围。
【错解】当x=0时,y=1;当x=4时y=33
∴当0≤x≤4时,y的变化范围是1≤y≤33
【剖析】错解是由于对求二次函数值的范围缺乏实质性的认识而造成的,事实上,抛物线在对称轴的左侧时,y随x的增大而减小,抛物线在对称轴的右侧,y随x的增大而增大,于是x=-b/2a=2/3时,函数取到最小值-1/3.
【正解】当x=-b/2a=2/3时,函数最小值-1/3,所以y的取值范围是-1/3≤y≤33
【矫正练习】
1.若A(-13/4,y1),B(-5/4,y2),C(1/4,y3)为二次函数y=x²+4x-m的图像上的三点,则y1,y2,y3的大小关系是_____.
2.心理学家发现,在一定的时间范围内,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间满足函数关系式y=-0.1x2+2.6x+43(0≤x≤30),y越大,表示接受能力越强。那么,学生在0≤x≤30这段时间内,接受能力y的取值范围是_____.
3.y=-x2+8x-12,在当x≤4时,y有最大值_____.
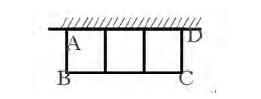
4.如图,在一面靠墙用长为8米的铝合金制成如图窗框,问窗框的宽和高各为多少米时,窗户的透光面积最大?最大面积是多少?若墙的最大可用长度为3米,则求窗户的透光面积最大?最大面积是多少?
通过易错题的练习,可以提高学生的审题、解题能力和题后反思能力,以起到事半功倍的效果,从而进一步提高数学学习效率。