摘 要: 计算思维的构建有助于帮助学生将实际问题转换为透明易懂的框架算法, 并借助计算机解决。以电影《疯狂动物城》中的兔子繁殖问题为例, 引出斐波那契数列, 引导学生将数学表达式转化成计算机编程语言, 进而通过Matlab软件进行问题的求解。
关键词: 计算思维; 斐波那契数列; Matlab;

Abstract: The construction of computational thinking helps students to transform practical problems into transparent and understandable framework algorithms and solve them with computers.Taking the rabbit breeding problem in the movie Zootopia as an example, the Fibonacci sequence is derived.This paper tries to guide students to translate mathematical expressions into computer programming languages, and then solve problems through MATLAB software.
Keyword: computational thinking; Fibonacci sequence; MATLAB;
计算思维最早是卡内基梅隆大学计算机科学系主任周以真教授提出的, 意在运用计算机科学的思维方式进行问题求解, 本质上源自数学思维。课堂上培养学生的计算思维, 第一要用计算的思维对要解决的问题进行分析和描述, 将其转化为一种数学上的语言表达;第二要在数学表达的基础上, 找到解决问题的方法 (也被称为是算法框架) ;第三要通过算法框架结合计算机, 转化成适合计算机运行的编程语言。
一、问题的提出
电影《疯狂动物城》中有一个关于兔子繁衍能力的细节。兔子Judy8岁的时候有275个兄弟姐妹, 离开兔窝镇的时候计数牌的数字在飞速增加。按兔子的繁殖能力 (兔子在第二月就成熟了, 第三个月初就可以繁殖) , 15年后Judy去Zootopia时, 她的家族会有多少成员? (兔子年龄寿命是5-12岁, 所以电影中所说的8岁有点拟人化了, 先暂时忽略掉)
二、Fibonacci数列的引入
Fibonacci数列[1]是数学家斐波那契以研究兔子繁殖为例研究的数列, 故称“兔子数列”, 又称为黄金分割数列。这个数列在物理、化学等领域都有广泛的应用。
根据这一数列, 结合实际情况先假设几个条件:
第一个月初有一对刚诞生的兔子;
第二个月之后 (第三个月初) 它们可以生育;
从第三个月开始每个月每对可以生育的兔子就会诞下一对新兔子;
兔子没有死去。
我们按照以上假设用图形的方式来展示前几个月兔子的繁殖的数目, 详见图1。
图1 兔子繁殖状态
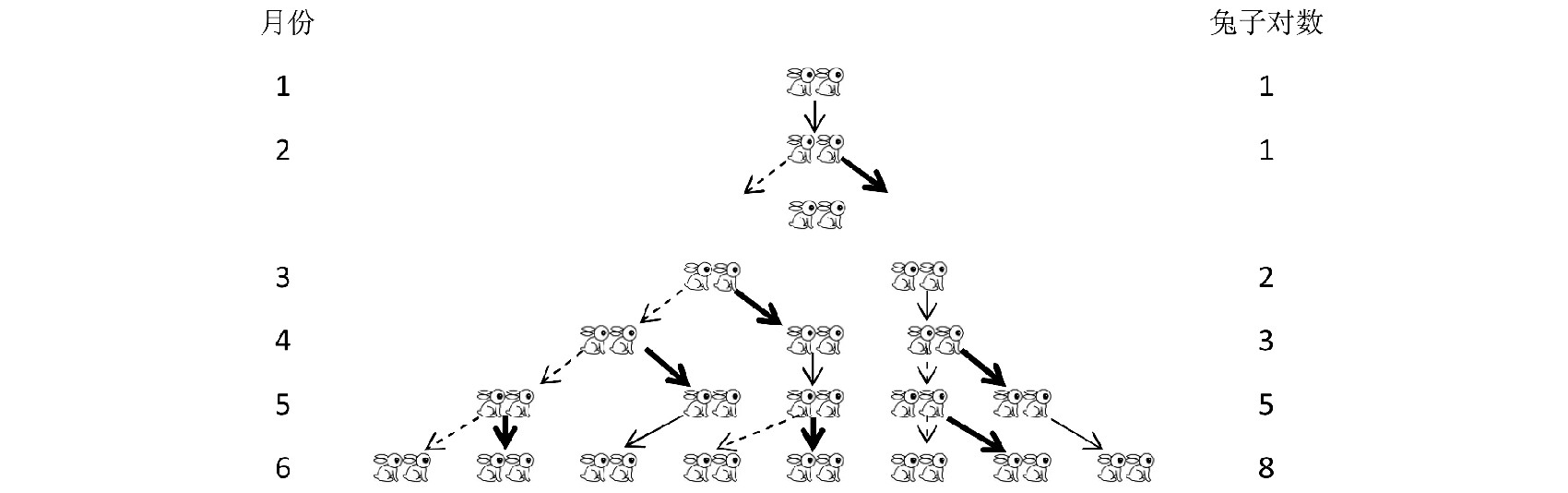
以上展示的数列形式就是Fibonacci数列, 用数列的通项表示为:
用表格列举法显示Fibonacci数列的前15项如表1所示。
表1 15个月的兔子繁殖状态

三、问题的解决
当Judy家庭成员人数是139对, 大约在数列的第12项, 则15年后即再过180个月, 也就是要求出Fibonacci数列的第192项, 采取递推的形式即可求出问题。
四、计算机matlab程序的实现
从这个数列的通项中可以看出这个数列是递推数列, 采用循环算法:

定义完数列后, 就可以想求第几项就求第几项, 如问题中要求第192项, 输入f (192) , 即可求得15年后Judy的家庭成员人数, 问题得以解决。
这是其中一种用matlab算法[2]编程实现的思路, 学生可以试着用学过的C语言[3]中的while语句来实现这种循环的递推关系, 也可以用学过的其它语言来解决这个编程问题。
五、课堂扩展
科学家研究Fibonacci数列后发现, 随着数列中n的取值无限增加, 前一项与后一项的比的极限:, 这个数是有名的黄金分割数。[4]黄金分割点是一种数学上的比例关系, 让生活中的事物具有完美的比例性。课后学生可以通过网络资料了解这一数列在自然界以及其它方面的应用和存在情况。
参考文献:
[1]郑英元.斐波那契数列[J].数学教学, 2009, (2) :49.
[2]曹艳华, 吕广红.几种求广义斐波那契数列的Matlab实现方法[J].大学教育, 2016, (1) :96-97.
[3]孙义欣, 宋大伟.斐波那契数列问题的C语言教学实施探讨[J].电脑编程技巧与维护, 2012, (16) :151-152.
[4]蔡克, 吴敏.黄金分割与斐波那契数列[J].九江职业技术学院学报, 2003, (3) :60-61.





