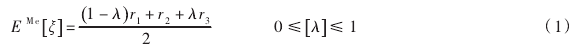模型中:M 为风险偏好指数-工期-完工概率评价指标;P 为计划工期的完工概率;T 为计算得到的工序活动施工工期;λ为决策者风险偏好指数;Q 为工序活动计划工期;σ为工期标准差;δ 为计划工期完工概率系数;S+S 表示工序活动之间的相关性;S*R 表示工序活动与风险因素之间的相关性;R+R 表示风险因素之间的相关性;Pi( i =)1,2,3分别表示受多种不确定性风险因素综合影响下,工序活动施工工期提前、正常、延期的概率;F ( T)为仿真工期频率分布曲线; f ( t)为仿真工期频率分布曲线拟合函数;Ti( i =)1,2,3分别为乐观持续时间、最可能时间、悲观持续时间;t为最可能持续时间施工工期的工期区间半径。
2.2 改进 PERT 改进PERT是一种基于仿真的风险分析模型,考虑了工序持续时间的不确定性,实现了计划工期的风险程度分析,并在施工进度风险分析中引入了决策者风险偏好指标。改进PERT方法主要克服了传统PERT方法的以下几个缺点:(1)传统PERT方法所考虑的三时估计值中的乐观持续时间和悲观持续时间主观性偏强。由于各个专家自身工作经验和水平不同,对悲观时间和乐观时间的理解和估计有很大差别,并且由于人们一般都倾向于留出一定的时间富裕量,故得到的三时估计更偏向于悲观。(2)传统PERT技术没有考虑到风险因素相互关系对工程进度造成的影响。传统PERT通过把各种风险因素影响赋给三时估计,主观性偏强,分析过于笼统,也没有考虑风险因素对工程进度的非叠加影响。(3)传统PERT没有考虑决策者风险偏好指标对于施工进度方案选择的影响,而实际上风险偏好指标的取值对于施工工期和计划工期完工风险都会造成一定影响。
2.3 施工进度风险贝叶斯信念网络 本文利用贝叶斯信念网络(BBNs)作为预测施工工期的方法,主要在于BBNs具有以下几点优势[16-17]:(1)BBNs是基于概率推理的数学模型,能够对不确定性和概率性的事件进行表达,可以从不完全、不精确、不确定的知识或信息中做出推理;(2)BBNs具有强大的不确定性问题处理能力,采用条件概率表达各个信息要素之间的相关关系;(3)BBNs在模型参数输入和输出上具有较大的灵活性;(4)BBNs能有效地进行多源信息表达与融合,能够将各类相关信息纳入到网络结构中,按节点的方式统一进行处理,有效地按信息的相关性进行融合;(5)BBNs是将多元知识图解可视化的一种概率知识表达与推理模型,可以将变量之间的关系以图形的形式直观显示出来。本文通过风险因素贝叶斯信念网络计算得出各工序活动在受多种不确定性风险因素综合影响下,其施工工期提前、正常、延期的概率。
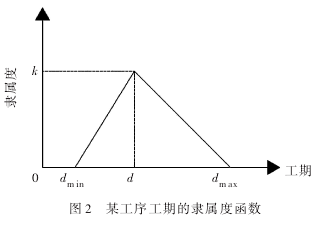
2.4 三角模糊数 三角模糊数由3个数值组成,分别为模糊数的上限、下限和可能性最大的值。以工期为例,用 Di表示工序 i的正常工期。在实际工程当中,设计人员可能会给出以最可能的工期 d,同时会根据实际情况给出最乐观工期,即最短工期 dmin,以及最悲观工期,即最长工期dmax,则此工序的工期用三角模糊数表示为 Di=(dmin,d,dmax),其隶属度函数如图2所示。
为了将三角模糊数(如(r1,r2,r3))转化为一实数,引入模糊测度Me方法[18]中的乐观-悲观指标来解决这一问题,其转化过程用下面函数表示:
式中:λ为决策者乐观-悲观指标(或决策者偏好指数),由决策者根据实际工程中对风险相关因素的评判进行确定。
当出现高风险因素时,λ取值较大;相反,若均为低风险因素,则λ取值较小。