
混流式水泵水轮机的比转数较低,而工作水头又较高,它的密封系统泄漏量的值直接影响机组的能量特性. 因为泄漏量的大小决定了机组的容积损失,而且泄漏会使密封腔内产生较大的压强,从而影响整个机组的稳定性能[1],同时它还是选择机组顶盖排水方式的重要参考依据,因此对机组泄漏量的计算是必要的. 在机组处于工作状态时,使用传统的试验方法对泄漏量进行测量非常困难. 传统方法一般依据相关理论,采用经验参数对其泄漏量进行计算,但这种方法对经验参数的依赖程度较高,并且计算的准确度较低.
目前 CFD 技术已成为水泵水轮机性能研究的一种重要方法. 王焕茂等[2]应用数值方法对水泵水轮机的驼峰区进行了模拟,并初步分析了驼峰区形成的原因; 刘锦涛等[3]应用 RNG k - ε 湍流模型对水泵水轮机在空载开度下的压力脉动进行了计算分析,对导致压力脉动的主要因素进行了说明; 张兰金等[4]、刘竹青等[5]、肖若富等[6]、纪兴英等[7]应用数值方法对水泵水轮机"S"特性方面的问题进行了研究; 尹俊连等[8]分别采用 URANS 和 DES 方法对水泵水轮机泵工况小流量区的压力脉动情况进行了计算,同时对比分析了 2 种计算方法. 然而,目前针对水泵水轮机密封间隙泄漏问题的研究还很少,大量的密封泄漏问题往往以单独的密封间隙为研究对象,例如: Tong 等[9]利用 CFD 数值模拟技术和传统试验方法对迷宫密封间隙泄漏现象进行了模拟和对比分析,对不同类型、不等间隙值的间隙流动进行了对比分析,验证了 CFD 数值方法的准确性; Jeffrey等[10]通过试验证明 CFD 数值模拟法描述间隙泄漏问题的可行性和准确性; 王炜哲等[11]对 2 种不同齿形位置的间隙流动进行了数值模拟,并对各自的密封性能进行了数值分析. 以含密封间隙的水泵水轮机全流道为对象,进行间隙泄漏方面的研究还存在着较大空缺. 文中分别采用理论公式法和 CFD 数值模拟法对水泵水轮机的泄漏量进行计算,并对计算结果进行分析.
1 问题描述
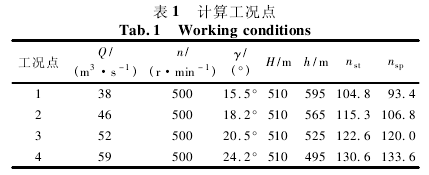
以某电站大型混流式水泵水轮机的原型机为研究对象,并采用 Pro/E 三维造型软件对其全流道进行三维几何建模,如图 1 所示. 图 2 为密封环的结构简图,其中间隙 1 为上冠与顶盖之间的密封间隙,间隙 2 为下环与底环之间的密封间隙. 水泵水轮机主要特征参数( 泵工况) : 转轮进口直径为 1 920 mm;转轮出口直径为 3 820 mm; 叶片数为 9; 活动导叶数为 20; 固定导叶数为 20. 表 1 为本次计算所选的工况点,其中,Q 为流量,n 为转速,γ 为导叶开度,H 为水头,h 为扬程,nst为水轮机比转数,nsp为泵比转数.

2 理论计算
计算水泵水轮机密封间隙泄漏,传统的方法是利用已有的圆管阻力系数,通过式( 1) 对泄流量 q进行求解[12]:

式中: μ 为流量系数; Hm为间隙两端的压力降; Fm为间隙的过流断面面积.
2. 1 流量系数 μ 的确定
文中所研究的水泵水轮机上、下间隙均采用迷宫密封,此类型密封系统的流量系数计算公式为

式中: Li为间隙的长度值; bi为间隙的宽度; fi为间隙的过流断面面积,fi= 2πRibi; λ 为计算因子,与间隙流动中的雷诺数和表面粗糙度有关,由于缝隙中的流动一般位于阻力平方区,故 λ 与雷诺数无关,可取 λ = 0. 04 ~ 0. 06. 文中为了能够准确地计算泄漏量,分别取 λ 为 0. 04,0. 05,0. 06,并加以比较.
因机组在水轮机与泵 2 种工况下密封间隙的高压侧均为泵工况下转轮出口处,故泵工况与水轮机工况下,迷宫密封流量系数 μ 是同等大小的.
图 3 为密封间隙示意图.

图 3a 为密封间隙 1 迷宫密封的局部放大图,其中,l 为间隙的长度,b1~ b5为不同间隙的间隙宽度,r1~ r5为间隙与叶轮中心的距离. 将图中所示参数代入式( 2) 中,可以计算出间隙 1 的流量系数: 当λ = 0. 04 时,μ = 0. 394 0; 当 λ = 0. 05 时,μ = 0. 385 7;当 λ =0. 06 时,μ =0. 377 8.
图 3b 为密封间隙 2 迷宫密封的局部放大图,其中,r1~ r9为不同间隙与叶轮中心的距离; h1,h2为间隙长度. 将图中所示参数代入式( 2) 中,可以计算出间隙 2 的流量系数: 当 λ = 0. 04 时,μ = 0. 219 1;当 λ = 0. 05 时,μ = 0. 211 2; 当 λ = 0. 06 时,μ =0. 203 8.
2. 2 间隙两端压力降 Hm的确定
间隙两端的压差值 Hm为扬程或水头 H 的一部分,对于现有种类的水轮机,这一部分水头可认为是稳定值[13],近似按比转数 ns的范围进行选取,即当ns= 60 ~ 150 时,Hm= 0. 6H; 当 ns= 150 ~ 250 时,Hm= 0. 8H.
根据表 1,在泵和水轮机 2 种工况下,机组比转数的变化范围在 60 ~150,故取 Hm= 0. 6H.
2. 3 过流断面面积 Fm的确定
对于迷宫密封间隙,Fm代表间隙进口处的过流断面面积,由此可以计算出间隙 1 的过流断面面积Fm= 13 176. 031 0 mm²; 间隙 2 的过流断面面积Fm= 6 202. 050 1 mm².
3 CFD 数值计算
应用 CFX 软件对含有密封间隙的水泵水轮机全流道模型进行数值模拟,通过对间隙 1,2 进、出口截面上的流量监测,得出间隙 1,2 的泄漏量具体数值.
3. 1 网格的划分
对于密封间隙流动的数值模拟,难点在于网格的划分. 由于密封间隙内的液体流动不是孤立的,与转轮内部的液体流动有着密切的关系,因此将其单独计算不能正确地模拟出其内部流动状态,但整体计算时,面临着小尺度网格与大尺度网格过渡的问题.
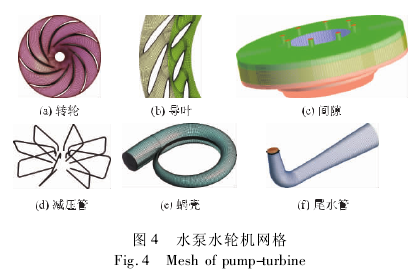
为了更好地解决此问题,文中应用 ICEM 软件,采用分块网格技术对整体模型进行了全流道六面体结构网格划分,整体网格数 3. 92 ×10^6,网格节点数4. 2 × 10^6. 在转轮和导叶之间添加一道圆周过渡层,以便进行间隙与机组之间的过渡连接,小尺度网格与大尺度网格之间的过渡生长率为 1. 2. 同时,为了满足计算对近壁网格的要求,对导叶、转轮近壁处进行了加密,具体网格如图 4 所示.
3. 2 求解方法及边界条件
考虑到密封间隙和转轮室的壁面弯曲程度较大,会造成其内部流线较大的弯曲,为了更好地处理这种高应变率及流线弯曲程度较大的流动,文中采用 RNG k - ε 模型[14]与连续性方程、N - S 方程构成封闭方程组.

式中: Gk为由于平均流速梯度引起的湍动能生成项; Gb为由于浮力引起的湍动能生成项; αk和 αε为k 和 ε 的反有效普朗特数; Sk和 Sε为 k 和 ε 的源项.
根据体积流量给定相应的质量流量作为进口边界; 出口边界为压力出口; 壁面采用无滑移壁面边界; 对于密封环与机组通过导叶、转轮之间过渡层连接,过渡层与导叶、密封环之间的边界条件设置成None,过渡层与转轮之间的边界条件设置为 FrozenRotor.
收敛标准: 当间隙 1 和间隙 2 的进、出口截面上的流量大小相等并且泄漏量不随计算步长的增加而发生变化时,认为本次计算已收敛.
4 计算结果及分析
图 5 为 CFD 数值模拟预测结果与已有原型机性能试验结果对比图. 从图中可以看出,应用 CFD数值方法预测的机组性能曲线与试验方法得到的性能曲线之间的吻合度较高,各项性能曲线之间的偏差小于 1. 6%,验证了文中采用的 CFD 数值模拟方法对机组性能预测的可行性、正确性.

图 6 为迷宫密封处速度矢量图. 由图可以看出迷宫密封的减压过程: 密封间隙处的液体速度较高,液体的压力能向动能进行转换,高速的液体在间隙出口处较大空间内形成涡流,使得液体涡损增大,各级密封间隙依次重复上述过程,最终达到降低液体压强的目的.
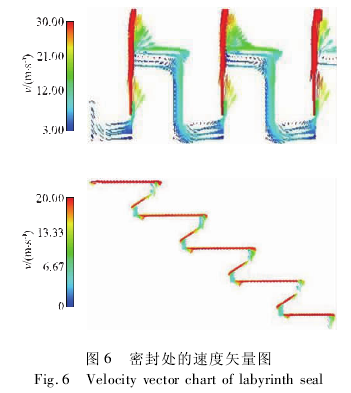
图 7 为机组分别在泵和水轮机工况下间隙 1,2泄漏量曲线图. 由图可知,由 CFD 数值模拟与理论方法计算出的泄漏量 q 随工况变化的趋势大致相同,2 种方法计算分析所得的机组泄漏量的最大差值在 25. 5%范围内; 间隙 1 处 2 种方法计算所得出的结果较为一致,而间隙 2 处则偏差较大,泄漏量最大偏差小于 10%,个别工况点处,此 2 种方法计算分析所得泄漏量的大小基本相同,曲线基本重合. 因此可以得出,对于机组泄漏量计算的理论方法和CFD 数值方法具有一致性,这也说明了 2 种计算方法具有一定的准确性,并且从侧面验证了理论方法中 Hm的估算值在合理的范围之内,同时还可以看出密封间隙内的泄漏量会随着间隙长度、宽度变化而相应增大或减小,也会随着迷宫密封齿数增多以及间隙形状复杂程度增加而变小. 与此同时,理论计算与CFD 数值模拟 2 种方法所得出的泄漏量的大小会有较大的偏差,理论计算的精确性也会由此下降.
在使用传统方法进行理论计算时,所用到的流量系数取决于经验参数 λ 的取值,并没有一个具体的规定和标准的原则,只能依靠人为经验在 0. 04 ~0. 06 范围内进行随机选取,这就使得流量系数的大小具有较大的不稳定性以及不确定性,最终导致计算出的泄漏量的值也不是很准确. 如图 7 所示,当 λ分别选取 0. 04,0. 05,0. 06 不同数值时,通过公式所计算出的泄漏量的理论值出现较大的波动,最大差值可达12. 2%,这说明使用理论方法计算泄漏量的大小具有一定程度的盲目性和随机性; CFD 数值方法计算出的间隙泄漏量是唯一的,具有较强的明确性.

在计算间隙两端的压力差值大小时,传统理论方法是以过往大量的统计数据为基础,利用比转数的大小进行压力差值的经验计算,这种方法只能简略粗糙地估算出压力降的值,不能非常精确地表达出在变工况下间隙两端压力降的分布规律,特别是在同一水头、不同导叶开度下的水轮机工况,如图7c,d 所示. 可以看出,变工况下由理论计算所得出的间隙两端压力降的值是相等的,从而使得泄漏量曲线为一条近似水平的直线; 而 CFD 数值模拟的泄漏量曲线则是一条随着流量的增大而逐渐上升的曲线. 因此,可以得出结论: 变工况下间隙两端的压力降的大小是波动的,且呈现出随流量的增大而逐渐上升的规律. 当机组实际运行时,随着导叶开度的增大,流量固然也会增大,机组内部压力场也会随之变化,而机组的泄漏量不会固定不变. 因此,理论计算法对泄流量的计算是不够准确的,只是给出了泄漏量的一个定性的变化范围,而 CFD 数值方法却得出了泄漏量变化与流量变化之间的规律,较为准确地描述了机组的泄漏问题.
对比泵工况下( 见图 7a,b) 和水轮机工况下( 见图 7c,d) 可以看出,2 种工况下 CFD 数值模拟的间隙 1 的泄漏量都比理论计算值略小,其泄漏量曲线与 λ =0. 06 的曲线较为接近; 而数值模拟的间隙 2的泄漏量却较理论计算值略大,其泄漏量曲线与 λ =0. 04 的曲线较为接近. 据此,可以归纳出参数 λ 选取的大体原则,即对宽度较小、长度较大、密封齿数较多且形状较为复杂的密封间隙,λ 应取较小值0. 04; 反之,λ 应取较大值 0. 06.
5 结 论
基于六面体结构化网格,应用 CFX 软件对含密封间隙的水泵水轮机全流道模型进行数值模拟,计算出的各项性能指标与试验性能指标吻合度较高,验证了数值方法对水泵水轮机间隙泄漏问题研究的可行性.
1) 基于 RNG k - ε 湍流模型的 CFD 数值方法可以用来模拟计算迷宫间隙泄漏的问题,且能够较为准确地预测水泵水轮机泄漏量的大小,从而得到机组泄漏量随工况变化的规律.
2) 基于含密封间隙的整机全流道数值模拟,考虑了机组的容积损失,提高了计算精度,可以更为准确地预测机组性能.
3) 应用理论方法对间隙泄漏量进行计算时,准确度会随着机组泄漏装置流量系数 μ 的减小而降低,因此,对于流量系数较小的可逆式水泵水轮机组,理论计算方法是不能对其泄漏量进行准确预测的.
4) 在等水头、变出力的水轮机工况下,水泵水轮机的泄漏量随流量的增大而增大; 在变扬程、变出力的水泵工况下,水泵水轮机的泄漏量具有随扬程的升高而增大的趋势.
5) CFD 数值模拟法能够较好地指导理论方法计算泄漏量,通过对 CFD 数值模拟结果的分析,可以总结出经验参数 λ 选取的大体原则,为其选取提供参考.
参考文献( References)
[1] 梅祖彦. 抽水蓄能发电技术[M]. 北京: 机械工业出版社,2000: 1 -10.
[2] 王焕茂,吴钢,吴伟章,等. 混流式水泵水轮机驼峰区数值模拟及分析[J]. 水力发电学报,2012,31( 6) :253 - 258.
Wang Huanmao,Wu Gang,Wu Weizhang,et al. Nu-merical simulation and analysis of the hump district ofFrancis pump-turbine[J]. Journal of Hydroelectric En-gineering,2012,31( 6) : 253 - 258. ( in Chinese)
[3] 刘锦涛,刘树红,孙跃昆,等. 水泵水轮机空载开度压力脉动特性预测[J]. 工程热物理学报,2012,33( 3) : 411 -414.
Liu Jintao,Liu Shuhong,Sun Yuekun,et al. Predictionof pressure fluctuation of a pump-turbine at no-loadopening[J]. Journal of Engineering Thermophysics,2012,33( 3) : 411 - 414. ( in Chinese)
[4] 张兰金,王正伟,常近时. 混流式水泵水轮机全特性曲线 S 形区流动特性[J]. 农业机械学报,2011,42( 1) : 39 -43.
Zhang Lanjin,Wang Zhengwei,Chang Jinshi. Flow ofpump-turbine on S-shaped region of complete characteri-stics[J]. Transactions of the Chinese Society for Agri-cultural Machinery,2011,42 ( 1 ) : 39 - 43. ( in Chi-nese)
[5] 刘竹青,孙卉,肖若富,等. 水泵水轮机"S"特性及性能改善[J]. 水力发电学报,2013,32( 2) : 257 -260.
Liu Zhuqing,Sun Hui,Xiao Ruofu,et al. S-shapedcharacteristics of pump-turbine and improvement on itsperformance[J]. Journal of Hydroelectric Engineering,2013,32( 2) : 257 - 260. ( in Chinese)
[6] 肖若富,孙卉,杨魏,等. 水泵水轮机预开导叶的优化分析[J]. 排灌机械工程学报,2013,31 ( 2) : 128- 131.
Xiao Ruofu,Sun Hui,Yang Wei,et al. Optimization ofmisaligned guide vanes scheme of pump-turbine[J].Journal of Drainage and Irrigation Machinery Enginee-ring,2013,31( 2) : 128 - 131. ( in Chinese)
[7] 纪兴英,赖旭. 低比转速水泵水轮机"S"区特性数值模拟[J]. 水动力学研究与进展,2011,26( 3) : 318- 325.
Ji Xingying,Lai Xu. Numerical simulation of the S-shaped characteristics of the pump-turbine[J]. ChineseJournal of Hydrodynamics,2011,26( 3) : 318 - 325. ( inChinese)
[8] 尹俊连,刘锦涛,王乐勤,等. 水泵水轮机泵工况小流量区压力脉动预测[J]. 工程热物理学报,2011,32( 7) : 1141 -1144.
Yin Junlian,Liu Jintao,Wang Leqin,et al. Prediction ofpressure fluctuations pump turbine under off-design con-dition in pump mode[J]. Journal of Engineering Ther-mophysics,2011,32( 7) : 1141 - 1144. ( in Chinese)
[9] Tong Seop Kim,Kyu Sang Cha. Comparative analysis ofthe influence of labyrinth seal configuration on leakagebehavior [J]. Journal of Mechanical Science and Tech-nology,2009,23( 10) : 2830 - 2838.
[10] Jeffrey J,MooreJ J. Three-dimensional CFD rotor dy-namic analysis of gas labyrinth seals[J]. Journal of Vi-bration and Acoustics,2003,125: 427 - 433.
[11] Wang Weizhe,Liu Yingzheng,Jiang Puning,et al. Nu-merical analysis of leakage flow through two labyrinthseals [J]. Journal of Hydrodynamics: Ser B,2007,19( 1) : 107 -112.
[12] 关醒凡. 现代泵理论与设计[M]. 北京: 中国宇航出版社,2011: 564 -619.
[13] 沙波夫 H M. 水电站的水轮机设备[M]. 黄明忠,徐纪方,译. 北京: 中国工业出版社,1964.
[14] Yakhot V,Orzag S A. Renormalization group analysis ofturbulence: Basic theory[J]. Journal of Scientific Com-puting,1986,1( 1) : 3 - 11.





