
0 引言
在轴流式水电机组中,顶盖不仅承担着转动部件的重量,机组运行过程中所产生的轴向推力也将通过顶盖法兰向周围混凝土基础传递;同时顶盖作为过流部件,其过流面承受着水压力的作用.因此,顶盖的刚强度性能将直接影响到整台机组的安全运行[1-2].
本文运用 ANSYS 软件,对某大型轴流式水轮机顶盖中存在的结构及动态特性问题,提出合理的改进方案.
1 电站基本参数
该电站的水头及相关参数如表 1 所示.
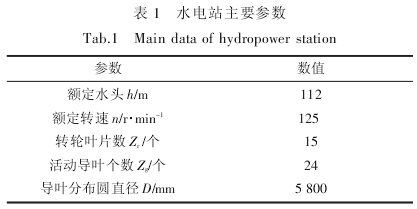
水轮机顶盖材料采用 Q235B,根据 ASME 标准,其材料性能及许用应力如表 2 所示.
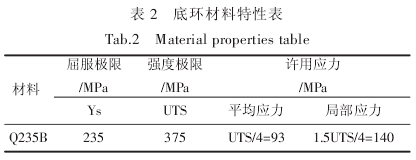
附加质量对顶盖的固有频率影响很大,为了保证计算的准确性,在分析顶盖自振频率时,考虑了顶盖上的相关部件质量因素,见表 3 所示.
2 有限元模型
2.1 模型
顶盖属于周期对称结构,共有 24 个导叶孔、12 个长筋板和 12 个短筋板.顶盖外缘法兰采用双上法兰结构把合型式,法兰之间分布 24 个小筋板.
在有限元模型中,考虑顶盖结构和载荷分布的周期对称性,切取包括两块幅向筋板 (1 长筋板和 1 短筋板) 和两个导叶孔的 1/12 顶盖扇形区域结构作为计算模型,选取每个节点具有三个自由度的 20节点六面体实体单元 SOLID95 划分网格以保证计算精度.
顶盖原结构如图 1 (a) 所示,经有限元计算发现此结构存在局部应力过高、水导处径向刚度较低以及动态特性较差的问题.分析可以知道,长筋板高应力是由于腰孔外侧倒角尺寸较小而导致,而短筋板与下环板连接处出现的高应力则是由于此处结构不连续所造成.针对这些问题,本文提出了降低局部应力和提高水导径向刚度的优化方案,将短筋板底端向内缩小 90 mm,辐向筋板厚度由 50 mm增至 60 mm,同时将长筋板腰孔外侧 R=100 mm 倒角增加到 R=250 mm,如图 1 (b) 所示.

2.2 边界条件
在顶盖剖切出的两个对称面上,为使位移协调一致,采用 couple 对偶约束边界约束条件;同时约束顶盖双上法兰结构中下侧法兰与座环把合螺栓分布圆节点 向自由度,为防止发生刚体位移,任选一节点约束其 向自由度.
2.3 工况及载荷条件
本次计算选取水轮机正常运行工况作为计算工况.工况中活动导叶处于全开状态,顶盖受到导叶下轴套的集中力与顶盖受到的水压力相对很小,可以忽略不计.因此,认为顶盖只受到水压力的作用.
水压力载荷如表 4 所示.

3 计算结果及分析
3.1 刚强度分析
本文对比分析了原结构与优化后结构在水轮机正常运行工况下的 Von Mises 应力结果.图 2 是两种结构的 Von Mises 应力分布图.原结构最大应力值出现在长筋板腰孔外侧,数值是 190.4 MPa.同时,短筋板与下环板连接处应力水平在 169.5 MPa左右,如图 2 (a) 所示.这明显大于材料许用应力值 140 MPa,不符合强度设计要求.

图 2 (b) 是优化后结构的 VonMises 应力分布图.从图中可知,最高应力出现在法兰结构约束位置,最大值仅是 67.2MPa,满足强度设计要求.对比两种结构综合变形,分别是 1.179 mm 和 0.979 mm,而顶盖最大变形一般不超过 0.2D/1 000=1.160 mm[3],原结构不符合刚度设计要求.而优化后结构刚度提高了 17.0%,足以说明优化后结构刚度性能优于原结构,且满足设计要求.
3.2 径向刚度分析
在水轮机运行过程中,水导轴承将机组运行中主轴传来的径向力和振摆力传递给顶盖水导处,水导的径向刚度决定着机组主轴的振动.本文运用ANSYS 对两种方案顶盖结构进行了水导径向刚度分析.选取一半顶盖结构作为计算模型,对称面上施加对称约束,法兰螺栓把合分布圆上约束 r、θ、z 三个方向自由度.设总径向力为单位力 F0,在水导处节点 R 方向上按余弦分布规律施加径向力.
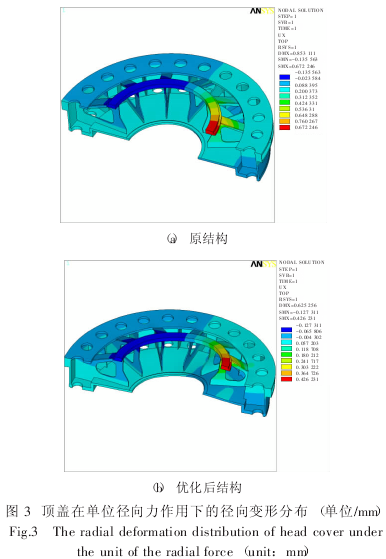
图 3 是两结构在单位径向力作用下的径向变形分布图,从而获得两顶盖径向刚度分别为:
原结构顶盖径向刚度:
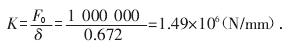
优化后顶盖径向刚度:
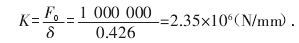
顶盖水导结构径向刚度应满足大于 1.66×106(N/mm),显然,原结构径向刚度较低,不符合设计标准,优化后结构满足设计要求.
3.3 自振频率分析
本文运用 ANSYS 有限元软件,采用循环对称子模型方法计算两个模型顶盖的自振频率.在计算过程中增加了活动导叶质量、控制环质量、水导轴承质量和主轴密封质量对顶盖固有频率的影响因素,不考虑水的附加质量对顶盖振动的影响.通过计算得到前 4 阶固有频率振型,频率值如表 5 所示.图 4 是顶盖原结构主要振型图.
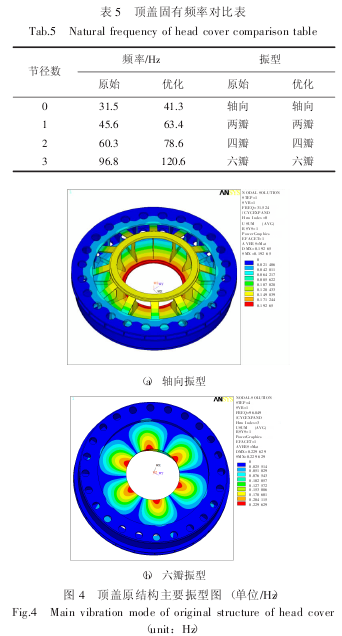
由于压力脉动的影响,整体轴向振动和节径数为 的顶盖自振频率是水轮机最危险的模态振动.这两种振动频率必须避开激振频率,否则会引起顶盖甚至整台机组的共振.引起顶盖振动的主要激振频率是:
转频与叶片个数的乘积;另外也应避开转轮与叶片之间的干涉频率,即由公式 n·Zg±K=m·Zr所确定顶盖振动的模态.其中活动导叶个数是 24 个,转轮叶片数是 15 个,可以确定关注的节径数为 K=3.所以,主要的激振频率是:转频×叶片个数 =125/60×15=31.25Hz;其 3 倍频为 93.75Hz.
从表 5 中可以看出,原结构轴向振动频率与转频与叶片个数乘积相等,节径数 K=3的六瓣振型频率与 3 倍频接近,这说明原结构存在极大的共振可能,动态特性较差.而优化后结构的固有频率能够避开激振频率,且避开范围大于 10%,不会引起机组共振现象.
4 结语
本文运用 ANSYS 软件,对某轴流式水轮机顶盖进行了优化设计,从顶盖刚强度、水导径向刚度及动态特性三方面对原方案和改进方案做了分析对比,结果表明:优化后方案在刚强度、径向刚度及动态特性方面均优于原始结构,满足设计要求,同时固有频率有效的避开了激振频率,不会引起共振现象.
参考文献
[1] 钟苏. 影响混流式水轮机顶盖刚强度的主要因素分析[J]. 大电机技术,1995 (3):36-40.
ZHONG Su. Large Electric Machine and Hydraulic Turbine,An-alazing Main Factors of Effecting Stiffness of Francis Turbine HeadCover,1995 (3):36-40.
[2] 庞立军,钟苏. 带圆筒阀的水轮机顶盖轴向刚度主要影响因素分析[J]. 大电机技术,2010 (1):54-57.
PANG Li-jun, ZHONG Su. The Main Factors Analysis for theAxial Stiffness of Ting Gate Structure Turbine Head Cover[J]. LargeElectric Machine and Hydraulic Turbine,2010 (1):54-57.
[3] 哈尔滨大电机研究所. 水轮机设计手册[M]. 北京:机械工业出版社,1976.





