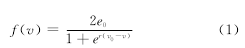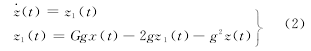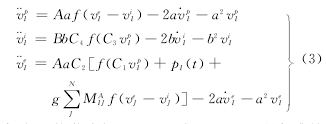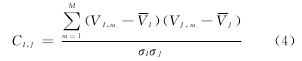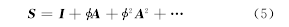0引言
随着生物和医学技术的进步,大脑结构和功能成像可以获得更加精确的数据,同时对大脑的研究不再局限于大脑子结构的形态和功能,更加注重各子结构之间的联系,因此,复杂网络理论成为研究大脑的有力工具.复杂网络理论起源于对规则网络和随机网络的研究,小世界模型和无标度模型的提出使复杂网络理论蓬勃发展,使复杂网络的观点开始进入人们的生活.复杂网络观点认为,脑网络可以分为结构网络和功能网络.构建脑网络时,将网络抽象为点集和边集,节点的对象是多层次的:神经元、神经元集群、脑皮层功能区域等都可以抽象为网络的节点,网络的边表示两个节点之间存在的某种关系.结构网络反映了脑皮层不同部分在形态学上的相似性或神经连接的多少;功能网络反映了脑皮层各部分神经元活动的动态协调性.节点的度、平均度、度分布、特征路径长度、聚类系数和介数等是度量网络的特征参数.研究表明,脑的结构和功能网络都表现出小世界特性,即平均路径长度很短,接近随机网络的平均路径长度;而聚类系数却比随机网络高得多,接近规则网络的聚类系数,并且结构网络对节点的损害表现出类似于无标度网络的抗毁性.复杂网络研究的一个重要内容是网络结构和功能的关系,脑网络研究也不例外.大脑皮层有两个重要的组织原则:结构分割和功能整合.这两个组织原则使大脑达到一个局部专注又整体协作的“经济”的工作模式.实现这两个原则要求结构网络和功能网络之间的协调,使大脑成为统一整体,因此对脑网络研究而言,结构和功能之间的关系十分重要.脑功能网络的拓扑结构特性会因为疾病发生变化,如癫痫患者在癫痫未发作时功能网络表现随机网络的特性,癫痫发作时功能网络表现为趋于规则网络的特性,阿兹海默症患者的脑功能网络相对于正常人来说出现了退化,因此脑的结构网络和功能网络的关系对大脑疾病的研究也具有重要意义.脑的结构和功能网络关系研究主要有两种方法:基于脑结构和功能成像研究同一个体的结构网络和功能网络,但受限于成像手段和被研究个体.基于结构网络模型和神经元模型的研究.由于这种方法完全基于模型,所以缺乏生理意义.本文综合了以上两种方法,采用同时基于脑的实验结构网络和神经元计算模型的方法.这种方法结合了前面两种思路的优点,因此得到的结果也更能让人信服.研究中采用的结构网络是通过解剖学得到的猫和猿猴脑皮层神经连接网络.网络中的节点采用神经元群模型,通过神经元群模型在脑结构网络中表现出的分层同步研究脑结构和功能网络的关系.
1猫和猿猴的脑皮层结构网络
构建脑结构网络可以分为三个步骤:
定义节点:利用先验图谱对脑皮层进行分区,每个分区作为一个节点.定义网络连接:基于结构磁共振的结构网络,根据网络节点形态学指标之间的统计关系确定连边;基于扩散磁共振的结构网络,根据纤维跟踪技术确定网络节点之间的神经连接;基于解剖学的结构网络,根据分区之间的神经连接多少确定连边.本文采用的脑结构网络是通过解剖学得到的哺乳动物的脑皮层神经连接网络.其中猫的脑结构网络是由53个区域、830条不同密度的神经连接组成的一个有向加权复杂网络,边的权重越大,说明连接两个区域的神经纤维越多.猿猴的视觉区域结构网络是通过注射追踪物获得的解剖学结构网络,共有30个区域、311个轴突连接.猿猴脑皮层视觉区域结构网络是猿猴脑皮层结构网络的一个子网络,同样地通过对示踪物的观测可以建立猿猴脑皮层网络,该网络具有71个节点、746条连边.猿猴的脑皮层结构网络都是有向无权网络,展现出自底向上的连通性层级:在微观层次上由相互作用的神经元构成网络,在中级层次上由突触和局部的脑区构成网络;在宏观层次上由大脑区域的神经纤维突起部分构成网络,是一个多尺度并且具备层级结构的网络.
2基于神经元群模型的脑功能活动模拟
大脑由神经元和它们之间的稀疏连接构成,具有多重的时间动态特性和空间尺度,由微观到宏观的各层次分别是神经元、神经元集群、脑皮层特定区域,脑皮层大规模组织和全脑.每一个层次都有其自身的 时空特性,因此从多重层次着手,用分 层同步的方法分析不同层次神经网络的结构和动力学行为,有利于清楚地观察拓扑结构和功能网络以及了解两者之间的关系.用动力学体制研究在不同时期的脑活动,首先要建立一个脑的计算模型,观察真实脑皮层连接网络的同步行为以及在系统层面上的全局动态组织和活动之间的关系.本文采用神经元群模型描述神经元集群的平均活动,然后通过模型显示一个定义明确的单个时间尺度的动力学系统,其节点的输入强度遵循全局网络拓扑产生的一个动力学模式.整个过程采用自下而上的方法,通过相互影响的神经元集群模拟网络节点,通过分层同步揭示动力学过程中脑结构和功能网络的关系.
2.1神经元群模型
神经元群模型的主要作用是反映神经元集群动力学行为,一个神经元集群包括两个子集:子集1包含椎体细胞组,接收来自子集2的细胞信号反馈;子集2是由局部区域的中间神经元组成,即获取兴奋信号和抑制兴奋信号的细胞,用来接收刺激的输出.模型主要描述集群的宏观变量:
vp表示锥体细胞突触后的平均膜电势,ve表示产生兴奋的中间神经元的平均膜电势,vi表示抑制兴奋的中间神经元的平均膜电势.邻域的神经元群模型和远距离的神经元群模型都接受一个全局性的刺激P(t),代表传入活动潜能的平均密度,引入静态非线性Sigmoid函数f(v)将平均膜电位潜能转化为反应潜能的平均脉冲密度.
式中,e0和v0对应于电位的发放率表示突触后的潜能,r表示Sigmoid函数的陡度.模型中主细胞和中间神经元之间的交互作用通过四个连接参数C1,C2,C3,C4来概述,它们代表突触连接的平均数目.兴奋和抑制的线性转化函数具有相同的形式,定义如下:
式中,在兴奋状态下,G=A,g=a;抑制状态下G=B,g=b.在对脑功能活动进行模拟时,将脑结构网络中的节点看作是神经元集群模型,各节点之间的耦合关系由脑结构网络确定,由N个耦合神经元群模型构成的系统中,第I个振子的动力学方程为:
式中,振子的激励为pI(t)=p0+ξI(t),ξI(t)是标准差D为2的高斯白噪声,p0=180,g为振子间的耦合强度.神经元群模型中的各参数取值如表1所示.
2.2功能连接的度量
脑功能网络的连接是不同脑皮层区域神经活动信号之间的动态的一致性,这种一致性可由神经活动在时间上的关联性和统计依赖性度量,主要分为线性和非线性两类,线性方法包括皮尔森相关、偏相关(时域)及偏相干(频域)等;非线性方法主要有同步似然性、互信息等.本文节点i和j之间的功能连接定义为对应离散时间序列VI=veI-viI和VJ=veJ-viJ的皮尔森关联.
式中,V和σ分别是节点神经活动时间序列V的平均值和标准差.
2.3数值模拟结果
本文进行了猫脑皮层、猿猴视觉皮层和猿猴脑皮层结构网络上的神经活动模拟.网络中耦合神经元群模型的初值取区间上均匀分布的随机值,通过4阶Runge-Kutta算法进行数值求解,求解的时间间隔为0.01s,模拟了10s时间长度的脑神经活动.图1、图2和图3分别给出了猫脑皮层、猿猴视觉皮层和猿猴脑皮层结构网络和对应的脑功能连接矩阵.
猫和猿猴的脑皮层结构网络都表现出层次性,可以分为几个内部连接紧密的子网络,这些子网络代表了执行相同功能的脑皮层区域.在对应的功能连接矩阵中,子网络内部节点之间有很高的关联强度,表明这些子网络内部的神经活动同步程度更高,子网络之间的同步程度较低,神经元群模型表现出分层同步的协同动力学行为.神经元群模型分层同步与脑皮层结构网络层次结构相吻合揭示了脑皮层结构网络和功能网络的一致性,脑结构网络的拓扑特征是脑功能的基础.为了进一步研究结构网络和功能网络层次结构之间的一致性,本文基于结构网络中节点的相似性定量计算了二者之间的相似程度.Leicht等基于节点邻居的重合程度定义了节点的相似性,网络的相似性矩阵S可以通过下式计算:
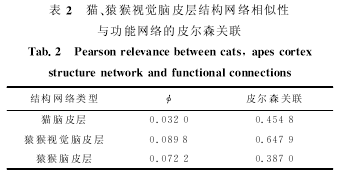
式中,A是网络的邻接矩阵,I是单位阵,?是控制参数,为保证S收敛,其应小于或等于矩阵A的最大特征值的倒数.我们分别计算猫、猿猴和猿猴视觉脑皮层结构网络的相似性矩阵,然后将矩阵按列存储为一维序列计算皮尔森关联,衡量三者的结构网络相似性矩阵和功能网络之间的一致性.表2显示了在不同的?分别取猫、猿猴和猿猴视觉脑皮层结构网络最大特征值倒数时,相似性矩阵和功能网络一致性的数量化度量.从表2可以看到,相似性矩阵和功能网络之间是正关联且具有较高的关联值,说明二者具有很高的相似度.数值实验的结果说明,功能相同的脑皮层区域通过一致的行为模式协作进行特定活动,不同功能的区域之间表现出不同的行为模式,脑皮层结构和功能的分割与整合通过分层同步行为得以实现.
3结论
本文通过耦合神经元群模型在脑皮层结构网络上的协同动力学行为研究了脑结构和功能网络之间的关系.在猫脑皮层结构网络、猿猴视觉脑皮层结构网络和猿猴脑皮层结构网络上,神经元群模型表现出了分层同步行为,一定程度上表明分层同步中的同步簇与结构网络层次结构一致,证明脑的结构网络是脑神经活动的基础,脑功能的分割和整合通过神经元的协同活动实现.结论能够部分说明脑的结构网络与功能网络的关系,对深入理解脑的神经活动具有重要意义.
参考文献(References)
[1]方小玲,于洪洁.复杂脑网络研究进展[J].力学进展,2008,37(4):611-613.
[2]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.
[3]Sporns O,Tononi G,K?tter R.The human connectome:A structural description of the human brain[J].PLoSComputational Biology,2005,1(4):245-251.
[4]Young M P.The organization of neural systems in theprimate cerebral cortex[J].Proceedings:BiologicalSciences,1993,252(1333):13-18.
[5]White J G,Shouthgate E,Thomson J N,et al.Thestructure of the nervous system of the nematodecaenorhabditis elegans[J].Phlilosophical Transactiona:Biological Sciences,1986,314(1165):1-340.
[6]Salvador R,Suckling J,Coleman M R,et al.Neurophysiological architecture of functional magneticresonance images of human brain[J].Cerebral Cortex,2005,15(9):1 332-1 342.
[7]Scannell J W,Young M P. The connectionalorganization of neural systems in the cat cerebral cortex[J].Current Biology,1993,3(4):191-200.
[8]Srinivas KV,Jain R,Saurav S,et al.Small-worldnetwork topology of hippocampal neuronal network islost in an invitro glutamate injury modlel of epilepsy[J].European Journal of Neuroscience,2007,25(11):3 276-3 286.
[9]Achard S,Bullmore E. Efficiency and cost ofeconomical brain functional networks[J].PLoSComputational Biology,2007,3(2):174-183.
[10]Ponten S C,Daffertshofer A,Hillebrand A,et al.Therelationship between structural and functional connectivity:Graph theoretical analysis of an EEG neural massmodel[J].NeroImage,2010,52(3):985-994.
[11]Scannell J W,Burns G A P C,Hilgetag C C,et al.The Connectional organization of the cortico-thalamicsystem of the cat[J].Cerebral Cortex,1999,9(3):277-299.
[12]Young M P.The architecture of visual cortex andinferential processes in vision[J].Spatial Vision,2000,13(2,3):137-146.
[13]Felleman D J,van Essen D C.Distributed HierarchicalProcessing in the Primate Cerebral Cortex[J].Cerebral Cortex,1991,1(1):1-47.
[14]Wendling F,Bellanger J J,Bartolomei F,et al.Relevance of nonlinear lumped-parameter models in theanalysis of depth-EEG epileptic signals[J].BiologicalCybernetics,2000,83(4):367-378.
[15]Zavaglia M,Cona F,Ursino M.A neural mass modelto simulate different rhythms in a cortical region[J].Computational Intelligence and Neuroscience,2010,2010(5):456140(1-8).[16]Heller D.A survey of algorithms in numerical linealalgebra[J].SLAM Review,1989,20(4):740-777.[17]Leicht E A,Holme P,Newman M E J.Vertexsimilarity in networks[J].Physical Review E,2006,73(2):026120(1-10).