作为因变量的缴费档次变动是典型的超过两类的有序离散变量, 本文采用有序Probit模型来分析。解释变量x1i—xmi构成向量Xi, 因变量为参保农民缴费档次变动分布Yi, Yi定义为分组变量, 因此, 定义一个连续因变量Y, 它是Yi的映射。此变量符合普通最小二乘法的条件, 与Xi构成线性关系:
(1) 式中, β'代表参数向量, ε为标准正态分布的随机误差。样本中参保农民按照4个等级给出缴费档次变动区间值。若Y≤0, 则对应等级1 (无变动) ;0<Y≤δ1, 对应等级2 (200元以下) ;δ1<Y≤δ2, 对应等级3 (200—300元) ;δ2<Y, 对应等级4 (300元以上) 。这里, δ1、δ2均为Yi值突变的临界点, 又称阈值, 和β'一样都是待估计参数。上述等级划分条件可改写成下列形式:
εi的概率密度为:

表1 变量的测量与描述
由于εi服从标准正态分布, 因此, 第i个样本出现于某等级j的或然率为:
四、计量结果分析
1. 参保农民缴费档次变动情况
调查结果显示, 缴费档次“没有变动”的占到了52.2%, 缴费档次增加了“100元”的占到了22.5%, 缴费档次增加了“200—300元之间”的占到了16%, 缴费档次增加了“300元以上”的占到了9.3%。由此可以判断, 在新农保实施一段时间后, 虽然一半以上的参保者仍然选择最低缴费档次, 但是提高缴费档次的参保者正在不断增加。这说明, 随着新农保制度的实施, 参保的“逆向选择”困局得到了一定程度的缓解, 但仍然存在。
2. 参保农民缴费档次变动影响因素
因变量是定序变量, 采用有序probit回归进行分析, 使用逐步回归法, 得到4个回归模型, 其中:模型1是控制变量对农民缴费档次变动的影响, 模型2加入了经济理性变量, 模型3又增加了认知激励变量, 模型4再加入制度激励变量。表2给出了具体分析结果。
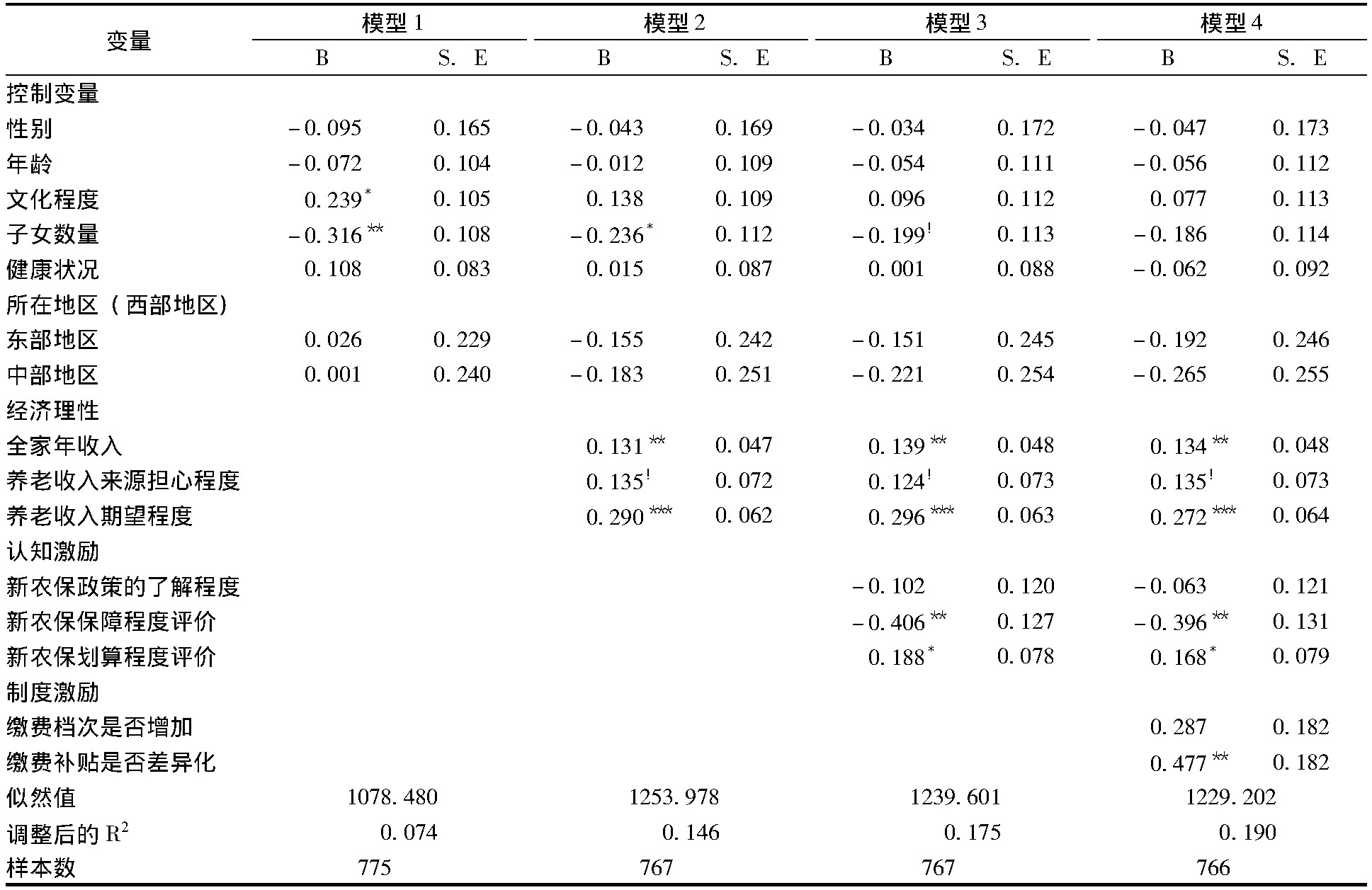
表2 农民参保缴费档次变动的有序probit回归模型估计结果





