第 4 章 生产性服务业集聚对长江中游城市群经济影响实证分析
4.1 模型设定及变量与数据说明。
本文通过第三章梳理出生产性服务业集聚对经济增长的影响机制,为了从实证来验证理论分析的正确性,将建立生产性服务业集聚对经济增长影响的计量模型,在此此前,本节首先对长江中游城市群生产性服务业集聚进行简单的测度和发展现状分析。
4.1.1 长江中游城市群生产性服务业集聚发展现状。
近年来,随着长江中游城市群经济的不断发展,生产性服务业的比重在国民经济中的比重不断加大,生产性服务业增加值占服务业增加值也已经超过了 75%,从生产性服务业就业人员来看,从事生产性服务业的人员逐年增加,这也表明长江中游城市群生产性服务业的不断发展,本文将使用区位商指标来测度和了解长江中游城市群生产性服务业集聚水平。区位商是指某地区某产业的产值(从业人员,企业个数)占该地区所有产业产值(就业人员,企业数量)的比重与区域整体的该产业(从业人员,企业个数)占区域总体所有产业产值(就业人员,企业数量)的比重之比,区位熵越大,表明产业集聚倾向越突出。数据处理后得出的长江中游城市群 28 个地级市的生产性服务业金融业集聚水平、交通运输仓储及邮政业集聚水平、科研、技术服务和地质勘查业集聚水平、科研、技术服务和地质勘查业集聚水平、租赁和商业服务集聚水平如附录 1-附录 5,此外下文也将计算构成长江中游城市群的江西省、湖北省、湖南省的具体生产性服务业的集聚水平。
可知长江中游城市群的金融服务业集聚水平在2003-2006年基本上没有变化,而从 2007 年的 1.35,上升到 2009 年的 1.50,然而到了 2010 年下降后,集聚水平上升到 2013 年的 1.63.
交通运输仓储及邮政业服务业集聚水平在2003-2013年发展很不稳定,从 2003 年的 2.11 下降到 2004 年的 1.97,进而又上升到 2006 的 2.24,最后从 2010 年的 1.88,逐年上升到 2013 年的 2.17.
科研、技术服务和地质勘查服务业集聚水平从2003年的0.87下降到 2005 年的 0.82,2006 年有所上升,但随后下降到 2008 年的 0.81,在 2009年又上升到 0.84,随后从 2010 年的 0.83 上升到 2013 年的 1.12.
信息传输、计算机服务和软件服务业集聚水平从 2003 年的0.40 上升到 2006 年的 0.51,随后下降到 2007 年的 0.43,进而在 2009 年上升到0.49,随后集聚水平发展很不稳定。
可知商业服务和租赁服务业集聚水平由 2003 年的 0.65 上升到2004 年的 0.66 进而下降到 2007 年的 0.38,随后上升到 2008 年的 0.64,进而下降到 2010 年的 0.61,随后开始逐年稳步上升到 2013 年的 0.84.
不管是金融业、交通运输仓储及邮政业等细分行业,还是总的生产性服务业,长江中游城市群的生产性服务业集聚水平在 2003 年-2009年的发展不太稳定,但从 2010-2013 年,均呈现稳步上升发展状态。
4.1.2 模型设定。
经济增长是一个相当复杂的过程,不仅会受到生产要素的供给及价格的影响,也会受到消费需求的影响,其中最基本的要素是便是劳动生产要素和资本的投入。
为分析各种生产要素对经济增长的影响,本文考虑影响经济增长的因素,建立起经济增长与相应的要素变量之间的经济计量模型,即把经济增长作为因变量,把劳动力投入,资本投入以及其他影响因素作为自变量来确定能够反映二者关系的函数。柯布-道格拉斯生产函数是经济学中使用最广泛的一种生产函数形式,通常学者们对经济增长的研究常采用柯布-道格拉斯生产函数,因此本文也将采用该函数作为研究经济增长的模型,它的基本形式如下:
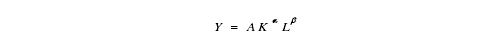
其中,A 表示表示广义的技术进步,包括知识、技术进步,产业结构优化、制度变迁等。K 表示资本,L 表示劳动力。由上文可知,劳动力投入和资本投入是影响经济发展最基本也是最重要的生产要素,而通过生产性服务业集聚促进经济增长的机制研究,我们可以知道生产性服务业集聚对经济增长的影响表现在通过知识溢出效应、产业关联效应、形成规模经济进而降低交易成本,最终提高了全要素生产率,极大地提出了区域经济的发展,全要素生产率的提高也就是劳动力生产率的提高及资本的有效利用,同时生产性服务业的产业间集聚和产业内集聚形成的专业化分工和经济多样化促进了技术创新,而技术的创新是基于知识存量的,知识存量的大小直接影响了技术创新。因此为考察生产性服务业集聚对长江中游城市群经济增长的影响,本文对柯布-道格拉斯生产函数模型进行了扩展,以适应研究发展的需要,扩展的柯布-道格拉斯生产函数的形式是:
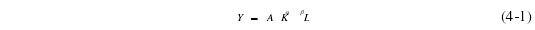
其中,i ,tG D P 表示城市 i 在 t 时期的总产出、i ,tK 表示城市 i 在 t 时期的资本投入、i ,tL 表示城市 i 在 t 时期的劳动力投入、i ,tS c a le 表示 i 城市生产性服务业的集聚规模、i ,tB 表示城市 i 生产性服务业集聚的总体外部性,其表达式如下:
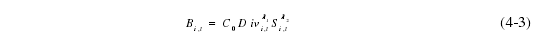
其中,0C 为常数;i ,tD iv 表示 i 城市生产性服务业的总体多样化程度、i ,tS 表示 i城市生产性服务业的专业化水平。
将公式(4-3)代入(4-2)可得如下表达式:

其中0m =ln C,公式(4-6)便是本文中用于定量分析生产性服务业集聚对长江中游城市群经济影响的计量经济模型。根据马歇尔外部性理论,生产性服务业集聚会产生规模经济效应,降低服务的生产成本、增加企业盈利空间,促进区域经济增长,因此本文将集聚规模 Scale 作为计量模型的一个自变量;而由上文的分析,生产性服务业集聚专业性和多样性也会促进区域经济的发展,所以本文选择专业化程度 S 和多样化水平 Div 作为影响经济增长的自变量。
4.1.3 变量与数据说明。
本文采用的样本为长江中游城市群 2003-2013 年 28 个地级市的面板数据,数据主要来自 2004-2014 年《中国城市统计年鉴》(1)经济增长:衡量经济增长的指标有经济增长率、GDP 、人均 GDP 、等,考虑到 GDP 与各变量的量纲数据相差太大,因此本文采用经济增长率来衡量经济的增长。(1)生产性服务业专业化:根据 Ezcurra,Pascual and Rapùn,生产性服务业专业化可表示为:
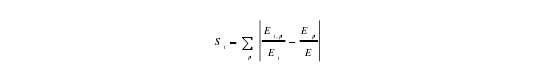
其中i ,pE 表示 i 城市 p 产业的就业人数,表示 i 城市的就业人数,表示整个长江中游城市群 p 产业的就业人数,E 表示整个长江中游城市群的就业人数。
(2)生产性服务业多样化:本文采用改进后的赫芬达尔-赫希曼指数 H-系数(Herfindal-Hirsh-man-index)来表示:
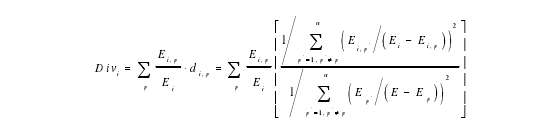
其中,iD iv 表示 i 城市生产性服务业的总体多样性程度,该指标越大表示多样性程度越高。当生产性服务业各部门所占劳动份额相同时,该指标达到最大值。
在计量模型中,该指标的正参数便表示存在雅各布斯外部性。
(3)生产性服务业集聚规模:目前,国内外测度服务业集聚水平的方法较多,包括区位熵、空间基尼系数、地理集中度指数,相比较而言区位熵指标比较简单易行,对数据的要求低,且能够衡量各地区分行业的产业集聚状况,是比较适合面板数据的计量分析,因此本文将采用区位商指标来衡量长江中游城市群生产性服务业集聚规模。
区位商是指某地区某产业的产值(从业人员,企业个数)占该地区所有产业产值(就业人员,企业数量)的比重与区域整体的该产业(从业人员,企业个数)占区域总体所有产业产值(就业人员,企业数量)的比重之比,区位熵越大,表明产业集聚倾向越突出。本文用每个城市生产性服务业就业规模占长江中游城市群总就业人口的比例来表示生产性服务业的集聚规模:
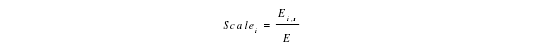
其中,iS a cle 表示 i 城市生产性服务业的相对规模,i ,sE 表示 i 城市生产性服务业的就业人数。
(4)知识存量:本文采用各地级市科学技术支出,科技支出指研究和试验发展阶段与科技活动有关的人、财、物、时间、信息等资源的投入科技经费的总量;(5)资本投入:本文采用各地级市年末固定资产投资总额;(6)劳动投入:从理论上讲,参与社会经济活动生产过程,创造价值的是劳动力付出的活劳动,因此,以劳动力的工作时间作为衡量劳动力投入的标准更加合适;但考虑到目前没有有效的统计方法来统计劳动者的工作时间,而且劳动的质量也存在不确定性,所以,本文采用中外学者的普遍做法,以年底劳动者的数量作为全社会劳动投入的替代变量,长江中游城市群各地级市劳动投入采用历年《中国城市统计年鉴》的年末就业人数。
4.2 模型估计及结果分析。
4.2.1 OLS 参数估计方法。
普通最小二乘法是目前回归分析中使用最广泛的估计方法,其基本思想是通过使残差平方和最小求出回归系数的估计值,因此本文也将采用普通最小二乘法估计来估计长江中游城市群生产性服务业集聚对区域经济增长影响模型。
4.2.2 描述性分析和单位根检验。
在进行单位根检验之前,本文先对各变量进行描述性统计分析,各变量的描述性统计分析结果。
计量经济理论表明,许多经济变量,尤其是面板数据大多数是非平稳的,用非平稳数据进行回归分析,会产生伪回归现象,因此需要先对各经济变量进行单位根检验,目的是为了检查每个变量在时间序列上是否是平稳的,这是避免出现伪回归的必然步骤。单位根检验方法有多种,其中应用最为普遍的是 ADF 检验,因此本文也将采用 ADF 单位根检验,本文利用 EVIEWS7.0 软件对各变量的原始值、一阶差分进行单位根检验,各个变量单位根检验的最终结果。
GDP、K、L、T、Scale、Div、S 的原数据序列均没有通过ADF 单位根检验,由此说明以上各变量均是非平稳序列。然后本文对 GDP、K、L、T、Scale、Div、S 进行一阶差分,并对各变量的一阶差分进行单位根检验,结果表明各变量的一阶差分序列均在 10%及以上显著性水平下通过 ADF 单位根检验,所以 GDP、K、L、T、Scale、Div、S 均是一阶序列。
4.2.3 面板数据的协整检验。
由于原序列均为一阶差分平稳,所以经济增长率与生产性服务业集聚各变量可能会存在某种平稳的线性关系,这个线性关系反映了各变量之间存在的长期的稳定均衡关系,也即协整关系。因此本文将对一阶差分后的数据做协整检验,如果存在协整关系,一阶差分后的数据做回归则不会出现伪回归的现象,可以直接用回归结果;如果不存在协整关系,则应该做稳健性检验,防止出现伪回归。本文用 kao 检验来检测原序列 GDP,K,L,Scale,T,Div,S 是否存在协整关系。ADF 的 t 值为-11.86,p 值为 0.000,拒绝原假设,原序列GDP、K、L、T、Scale、Div、S 存在长期的协整关系,因而可以继续做回归分析。
4.2.4 面板数据的回归结果。
本文通过对计量模型使用 OLS 估计,得出其实证结果。
4.2.5 回归结果分析。
从方程的估计结果可以看出,R-squared 为 0.932558,说明本文的计量模型拟合度较高,解释变量生产性服务业集聚规模的 p 值为 0,其在 5% 水平显著,表明生产性服务业集聚规模对长江中游城市群经济增长具有明显的正向效应,对经济增长 GDP 的影响为正,变量集聚规模的系数为 0.668,表明生产性服务业集聚规模每增加 1%时,经济增长率就增加 0.668%,从 GDP 的回归结果与长江中游城市群的经济发展情况基本相符。解释变量生产性服务业集聚多样性水平的 P为 0,其在 5% 水平显著,表明生产性服务业集聚多样性促进经济增长,从其系数 3.794766 来看,生产性服务业多样性程度每提高 1%个点,经济增长率就增加3.794%,该结果与本文第三章的理论分析结果相一致。而解释变量生产性服务业集聚专业化的 P 值为 0.6673,其在 1%水平下不显著,说明生产性服务业集聚专业化对经济增长的影响是负向作用,其与本文第三章理论分析中生产性服务业集聚专业化促进经济增长的理论分析结论相反,其原因将在第五章结论里面做深入的剖析。根据实证结果,生产性服务业集聚专业化每增加 1%时,经济增长率将减少 0.0096%.但综合生产性服务业集聚专业化和多样化水平,其总的效应仍然是促进经济增长的。而对于本文引入的知识存量解释变量,其 P 值为 0.0002,其在 5%的水平下显著,由其系数 0.056 可知,当科技支出水平每增加 1%时,经济增长率就增加 0.056%.以上是本文对生产性服务业对长江中游城市群经济增长影响的计量模型回归结果的分析,第五章也将继续从微观上分析其结果并将得出相关结论。





