
21 世纪是知识经济和信息经济时代,也是以数据分析为重要内容的大数据时代,在这个时代中数学技术的重要性日渐凸显,并以前所未有的速度向其他技术领域渗透,特别是数学技术与计算机技术的结合,已经成为当代高新技术的重要内容。美国学者 E·David 曾说,“数学在经济竞争中是必不可少的”。数学的革命性发展促进了数学教育的根本变革,数学建模、数学实验等成了高层次人才必备的基本能力,为此,应探究数学模型和数学实验的关系,以推进数学教育改革,培养学生“用数学”的能力。
一、数学建模概述
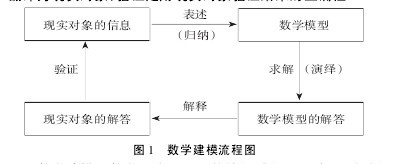
数学模型是为了描述客观事物的特征和内在联系,用字母、数字或其他数学符号建立的等式、不等式、图标、框图等数学结构表达式。数学模型能解释某些现实性问题,预测对象的发展状态,或为解决实际问题提供最优决策。数学建模是为实现特定目的而建造数学模型的过程。数学建模可以通过表述、求解、解释、验证几个阶段,实现现实对象到数学模型再到现实对象的循环。
如图 1 所示,表述是把实际问题翻译为数学问题,然后用数学语言解释实际问题; 求解是用科学的数学方法解答数学模型; 解释是用数学语言把答案翻译为现实对象; 验证是用现实对象验证结果的正确性。数学建模是数学理论运用于其他领域的切入点,对创新数学教育、培育创新精神具有重要意义。在数学教学中,教师可以引导学生弄清问题的本质、解决问题的方法途径等,让学生建构数学模型,或将实际问题归纳为某类数学模型,这样有利于培养学生的创新意识、创新精神,建立以解决问题为中心的教学模式。对同一案例可以用不同的数学方法、建模思路来解决,这样能拓宽学生的数学思维,激发学生的学习兴趣,形成“问题———探究———解答———问题……”的开放式教学模式,使数学教学向实践、社会、生活等延伸。【图1】
此外,数学建模有利于强化实践教学。学生要用数学知识解决实际问题,就需要建立数学模型,在建立数学模型时需要广泛搜集资料、查阅问题背景、用计算机模拟计算,这有助于培养学生的创新精神和科研能力。因而,在数学教学改革中,应渗透建模思想,学习建模方法,嵌入数学模块,将数学建模融入数学教学的全过程,培育学生的创新精神、实践能力、分析与解决问题的能力。
二、数学实验概述
数学实验是从指定的实际问题出发,借助计算机和数学软件进行数学运算、证明猜想、模拟仿真、显示图形等以及解决实际问题、探索数学规律的数学实践活动。数学实验以学生为主体,以实际问题为载体,以数学软件和计算机为工具,以数学建模为过程,以优化数学模型为目标,将抽象的数学理论变成了生动具体的可视性学科,实现了数学建模的发展和延伸。同时,数学实验也是实际问题与数学理论之间的桥梁和纽带,在提出猜想、验证定理、解决问题等方面发挥着重要作用。
数学实验课是利用计算机技术培养学生“用数学”能力的课程,它以学生为主体,以探索和创新为首要原则,让学生去体验、探索、实践,有助于提高学生的动手能力、思维能力和观察能力,提升学生的综合素质。数学实验课主要涉及数值计算、数理统计、优化方法三部分内容,通常以 MATLAB 数学软件平台进行各种运算,以数学方法安排课程内容,以数学建模引入问题和方法,整个课程从建模初步练习开始,到建模综合练习结束。随着计算机技术的快速发展,计算机的运算功能、图形功能日益强大,数学软件变得更加丰富,这使数学实验摆脱了机械性的符号演算,可以通过计算机进行观察、联想、类比等探讨规律性结果,这为数学实验教学创造了良好条件。
三、数学建模与数学实验的关系分析
( 一) 数学建模与数学实验的联系。数学实验与数学建
模的关系就是学数学和用数学的关系,学数学是研究、学习数学,用数学是以数学为工具来分析和解决实际问题,两者之间相互联系,相互促进,用数学是数学发展的原始推动力,学数学是数学发展的内在动力。
数学实验是高校数学教育的重要课程,侧重于培养学生应用数学的能力,数学建模是数学实验的应用与升华,是数学理论与数学实验相结合的产物。数学建模用 Matjematocal、Maple、Matlab 等软件包为数学实践课程创造了条件,使数学问题变得直观形象,便于理解和掌握; 数学建模促使数学学科不断向社会科学与自然科学渗透,也使数学实验被提到了新高度。另一方面,数学模型的建立与求解离不开数学实验,因为许多数学模型是抽象的、复杂的,只有通过数学实验,才能进行数值求解和定量分析。
( 二) 数学建模与数学实验的区别。数学实验和数学建模
并不相同,数学实验是学习数学的方法,以培养学生的动脑、观察、动手能力为目的,借助数学软件来验证和应用数学规律; 数学建模是运用数学的手段,以培养学生解决实际问题能力为目的,有助于提升学生的创新思维。就课程设置而言,数学实验课是理工类专业的四门数学基础课程之一,而数学建模课则多为数学选修课; 在数学类专业中,数学实验课多被放置于计算、优化、统计等课程之中,数学建模课多为必修课。数学建模课以实际问题的建模、模型结果的解释应用为主要内容,包含着丰富的建模案例,但很少涉及数学模型求解; 数学实验课介绍了数值计算、数据统计、方法优化等数学软件,侧重于用计算机、数学软件进行数学模型求解,涉及的实际问题较为简单。
( 三) 数学建模与数学实验的融合。数学实验与数学建模
都以培养学生创新能力、解决实际问题的能力为目标,这两门课程的融合有助于提升学生的创造思维、竞赛意识、创新意识与应用能力和整体素质,推进学生的全面发展,推进数学教学创新。传统数学实验是偏重学习的验证性实验,而数学建模与数学实验的融合能够使学生掌握 MATLAB、SAA、LINGO 等数学软件,并利用这些数学软件建立数学模型、解决数学问题,有助于提高学生分析和解决问题的能力,提升学生的综合素质。同时,“数学实验”与“数学建模”的融合有助于开展讨论式、研究型、实践案例式等开放式教学,解决传统教学中“重理论,轻实践”的问题,激发学生的数学兴趣,提高数学教学效率。
数学建模是沟通数学与其他学科的桥梁和纽带,也是推进数学发展的重要方式,将数学建模思想融入数学实验课之中,有助于学生运用数学技术和计算机软件解决实际问题,推进高校数学教学改革。
【参考文献】
1. 张学哲. 数学建模·数学实验·数学创新[J]. 湖北民族学学报( 自然科学版) ,2001,2
2. 秦宣云,李学全. 对数学实验课教学的认识以及教学过程实施方法[J]. 工科数学,2002,18( 6)
3. 楼建华. 数学建模与数学实验[J]. 黑龙江高教研究,2003,3
4. 徐兆棣,李晓毅. 数学建模与数学实验的交互关系[J]. 沈阳师范大学学报( 自然科学版) ,2010,3





