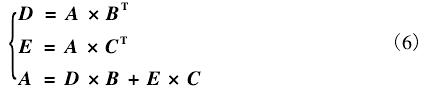当F(x,y)= 1时,在绞综穿 综区域内 可 用式(5) 表示 此 处 是 绞 经 经 组 织 点 还 是 地 经 经 组织点:

式中:x∈N且1≤i≤W1,y∈N且1≤y≤R1.
3. 2绞经花纱中各部分的数学关系
经分析,可以建立的数学关系如式(6) 所示。
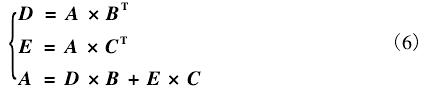
BT和CT代表绞综穿综及绞经所穿平综矩阵、地经所穿平综矩阵的转置矩阵。在计算D和E的过程中,有时会出现某些元素大于1,这是由于将基综提升作了重复运算造成的。所若D(x,y)> 1或E(x,y)> 1则令D(x,y)= 1或E(x,y)= 1即可;在 计算A的过程中,有时A中也会出现大于1的元素,若A(x,y)> 1,则令A(x,y)= 1.因为在计算绞经经组织点时,用上述公式重复计算了1次,因此可能会出现大于1的元素。
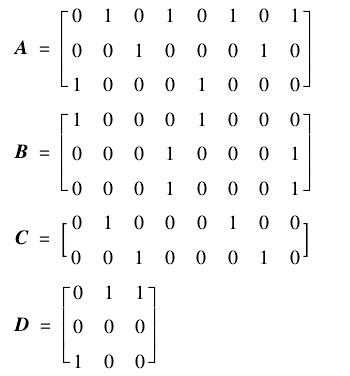
以图8(f) 中三经绞地斜纹花纱的地部组织为例,验算上机图中各部分的数学关系如下。

 4结 论
4结 论
本文以纺织史和丝绸考古成果为基础,按照织物组织结构对宋代绞经花纱进行分类,分析织造机具的形制推断出宋代绞经花纱的织造工艺。对比宋时机构与现代机构,按照新型纱罗提花机工作原理绘制宋代绞经花纱上机图,用矩阵表达上机图各部分并定义各矩阵之间的逻辑运算,建立数学模型。本文研究成果为对古代绞经织物与现代织机及CAD配合系统设计的实现提供了理论依据。
参考文献:
[1] 蔡欣。宋代绞经丝织物研究[J].丝绸,2016(2) :61 -72.CAI Xin. Study on warp twisted silk fabrics in SongDynasty[J]. Journal of Silk,2016(2) :61 - 72.
[2] 镇江博物馆。江苏金坛南宋周瑀墓发掘简报[J].文物,1977(7) :18 - 27.Zhenjiang Museum. A bulletin on the excavation of thetomb of Zhouyu of the Southern Song dynasty,Jintan,Jiangsu[J]. Cultural Relics,1977(7) :18 - 27.
[3] 福建省博物馆。福州南宋黄昇墓[M].北京: 文物出版社,1982:86 - 92.Fujian Museum. Thirteenth-Century Tomb NearFuzhou[M]. Beijing:Cultural Relics Press,1982:86 - 92.
[4] 陈晶,陈丽华。江苏武进村前南宋墓清理纪要[J].考古,1986(3) :247 - 260,转268.CHEN Jing,CHEN Lihua. A summary of the excavation ofthe tomb near Wujin of the Southern Song,Jiangsu[J].Archeology,1986(3) :247 - 260,and 268.
[5] 周迪人,周旸,杨明。德安南宋周氏墓[M].南昌: 江西人民出版社,1999:41 - 42.ZHOU Diren,ZHOU Yang,YANG Ming. Thirteenth-Century Tomb at De' an in Jiangxi[M]. Nanchang:Jiangxi People's Publishing House,1999:41 - 42.
[6] 顾苏宁。高 淳 花 山 宋 墓 出 土 丝 绸 服 饰 的 初 步 认识[C]/ /南 京 市 博 物 馆。南 京: 江 苏 人 民 出 版 社,2008:52 - 68.GU Suning. A study of the silk costume excavated fromthe tomb of Hua Moutain of the Song dynasty,GaochunCounty[C]/ / Nanjing Municipal Museum. Nanjing:Jiangsu People Publishing Ltd,2008:52 - 68.
[7] 南京市博物馆,中国文化遗产研究院,敦煌研究院,等。南京报恩寺遗址地宫文物保护研究[M].北京:文物出版社,2014:62 - 87.Nanjing Municipal Museum,Chinese Academy ofCultural Heritage,Dunhuang Research Academy,et al.A Study of the Protection of Cultural Relics Eexcavatedfrom the Underground Palace Historic Site of Bao' enTemple,Nanjing[M]. Beijing:Cultural Relics Press,2014:62 - 87.
[8] 赵丰。古代纱罗织物及其对现行组织学的启示[J].浙江丝绸工学院学报,1986,3(4) :50 - 55.ZHAO Feng. Ancient leno weaves suggestive ofextending the range of modern leno weave[J]. Journalof Zhejiang Institute of Silk Textile Technology,1986,3(4) :50 - 55.
[9] 陈国安。浅谈衡阳何家皂北宋墓纺织品[J].文物,1984(12) :77 - 81.CHEN Guo' an. A study of textiles excavated from thetomb of Hejiazao Moutain of the Northern Song dynasty,Hengyang[J]. Cultural Relics,1984(12) :77 - 81.
[10] 徐国华。从机织原理探讨古代提花技术的发展[D].上海: 华东纺织工学院,1981:11 - 12.XU Guohua. The developments of techniques for patternweaving in ancient China based on weaving prin-ciple[D]. Shanghai:East China Institute of TextileScience and Technology,1981:11 - 12.
[11] 史文训。中国古代绞纱织制技术及其发展[D].杭州: 浙江丝绸工学院,1985:50 - 56.SHI Wenxun. The guaze weaving technique and itsdevelopment in ancient China[D]. Hangzhou:ZhejiangInstitute of Silk Textile Technology,1985:50 - 56.
[12] 罗群。飘渺变化的“宋”罗[J].丝绸,2012(4) :52 -56.LUO Qun. Leno weaving techniques in Song Dynasty[J]. Journal of Silk,2012(4) :52 - 56.
[13] 赵承泽。中国科学技术史( 纺织卷) [M].北京: 科学出版社,2002:241.ZHAO Chengze. History of Science and Technology inChina(Textile) [M]. Beijing:Science Press,2002:241.
[14] 顾平。织物结构与设计学[M].上海: 东华大学出版社,2006:137.GU Ping. Fabric Structure and Design[M]. Shanghai:Donghua University Press,2006:137.
[15] 张国辉。用普通织机开发花式纱罗产品[J].纺织学报,2005,26(6) :97 - 98.ZHANG Guohui. Development of leno brocade productswith ordinary loom[J]. Journal of Textile Research,2005,26(6) :97 - 98.
[16] 詹忻,祝成炎。纱罗组织数学模型的实现[J].纺织学报,2009,30(1) :46 - 50,59.ZHAN Xin,ZHU Chengyan. Realization of mathematicalmodel for leno weaves[J]. Journal of Textile Research,2009,30(1) :46 - 50,59.
[17] 赵良臣,闻涛。织物组织设计中的综合和分解算法[J].纺织学报,2004,25(5) :83 -84.ZHAO Liangchen,WEN Tao. The comprehensive anddecomposing algorithm in dobby weave design[J].Journal of Textile Research,2004,25(5) :83 - 84.