4 构建 ZK 公司软件开发项目风险评估模型
4.1 构建评价指标集
根据上述理论,风险评估首先需要进行风险识别。在本人作者主持下,连同 ZK公司管理层,将运用到风险识别的相关方法或工具,依据公司的实际情况(参见第 3章),对公司软件开发项目管理过程的风险因素进行识别,然后简化关键因素后构建一套评价指标集,为下一步的风险估计做准备。
ZK 公司为控制软件产品的质量,在各个软件开发项目实施过程中基本上都是采用传统瀑布型软件生命周期开发模型,如图 4-1 所示。
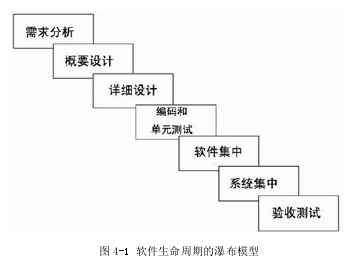
在此软件生命周期的模型框架下,我们以 ZK 公司技术经理为核心,运用流程图分析法(参见章节 2.2.1),基于公司长期习惯的软件开发项目管理流程为分析对象,将与公司的软件开发项目各种活动有影响的风险关键因素罗列出来,相关风险点见表 4-1所列。初步罗列出来的风险点,显然有一定的局限性,这是由于技术部较少参与到公司非技术性的管理工作中。
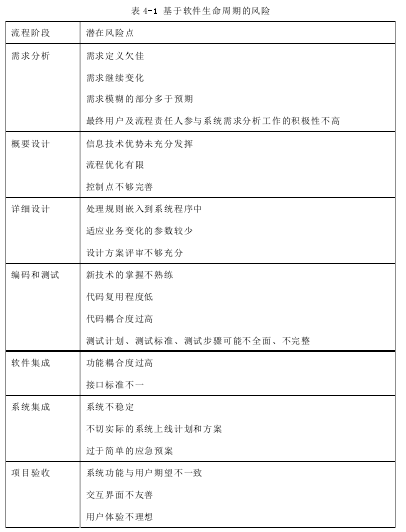
ZK 公司同时也注意到,风险管理应该是在所有的软件开发项目过程中持续进行的,所以还结合了 SEI 的 CRM 模型(参见章节 2.1.3)进行风险识别。同时,基于中小企业的实际管理特点,在项目管理和风险管理中不可能有太多的资源和繁杂的流程,所以必须去繁就简。公司全体人员集中在一起,采用头脑风暴法(参见章节 2.2.2)对公司的软件开发项目过程中主要的风险因素进行识别。在此风险识别过程中分两个层次进行。
在管理层,以公司领导和部门经理为主,体现公司的实际情况以及以往的经验,经过管理层的讨论,最后从宏观层面确定了 ZK 公司软件开发项目风险评估模型的 6个综合指标:人员因素、技术因素、管理因素、环境因素、资源因素、质量因素(见表 4-2 所列)。这 6 个综合指标的意义在于,能从宏观和中观的层面反映公司的普遍情况,在同一时点公司对不同的项目产生的影响基本相同,而在某一个不长的时间段内(如半年或 1 年)这些因素之间的关系不会出现太大的变化,对相同项目不同的时点产生的影响基本相同。只要公司的经营状况没有发生重大改变,这些综合指标相关权重在确认后,在相当一段时间内是相对稳定的,不需要在对每个项目进行评估时重新估算。
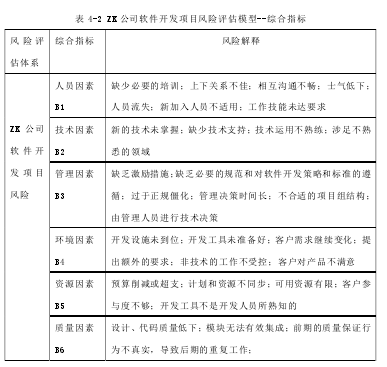
与此同时,我们组织公司内部的所有技术开发人员,针对软件开发项目过程中的具体风险,从操作层面上参考 Boehm 的“十大风险因素清单”(见表 2-1)以及 SEI 的风险提问单分类(见表 2-2),对公司的软件开发项目过程中的风险因素进行识别。经过讨论,最后从操作层面确定了 ZK 公司软件开发项目风险评估模型的 16 个评价指标(见表 4-3 所列)。这些评价指标的意义在于可以在任何时点对公司正在实施的任意一个软件开发项目进行逐项评价,而且不同的时点和不同的项目,评价结果可能都不同,能够真实反映项目在评估时间的实际风险。
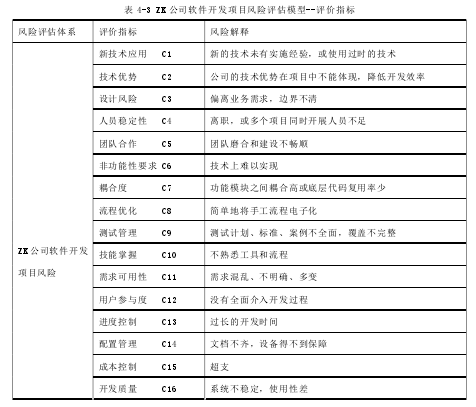
4.2 运用 AHP-FCE 构建评估模型
4.2.1 构建层次结构模型
在上述综合指标和评价指标确定后,采用层次分析法(AHP,参见章节 2.2.4)的思路,将 ZK 公司软件开发项目风险评价体系分为三个层次:第一层:目标层 A,ZK 公司软件开发项目风险第二层:综合指标 B,(B1--B6 ,见表 4-2 所示)第三层:评价指标 C,(C1--C16,见表 4-3 所示)在此三层体系的基础上,采取专家调查法(参见章节 2.2.3)确定各层指标之间重要相关性。专家组由 ZK 公司领导、技术部经理、外单位资深高工组成,本文作者负责调查问卷设计和调整,公司行政部采取电子邮件方式向专家发送并回收调查表。同时为了简化评价体系,将大多数专家都认为相关度不大的指标之间直接不作关联。在多次反复收集意见后,逐渐形成相对统一的指标相关性,从而获得 ZK 公司软件开发项目风险评价的层次结构模型,见图 4-2 所示:
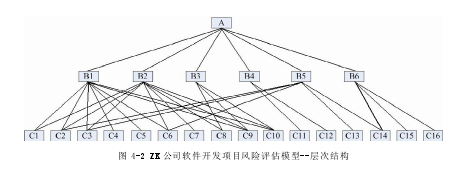
4.2.2 确定 B 层各综合指标的权重
在层次结构模型确定后,继续按上述方式采用专家调查法(参见章节 2.2.3)获得各指标间的两两比较矩阵。指标间采用 1-9 的标度(参见表 2-3)表示这两个指标之间对于对上一层某个指标的相对重要性,由各专家独立完成,然后采取平均值取整的方法最终得到关于项目风险(A)的综合指标(B1--B6)两两比较矩阵 A-B,如表 4-4 所示:
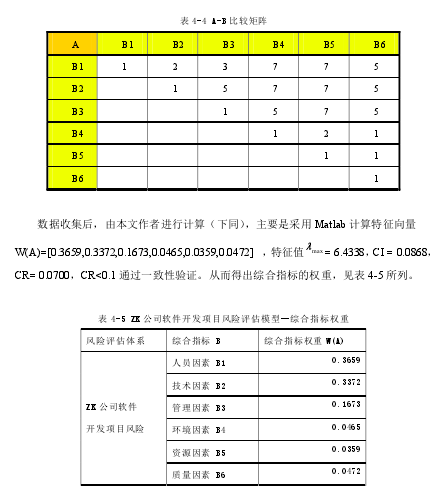
从该表可以直观看到各指标的风险排序,和 ZK 公司管理层的预期一致,符合公司实际情况。其中,人员因素和技术因素的权重比较突出,这和中小企业的特点相匹配,开发团队的人员本来就不多,个别人员的素质和流动对项目影响很大,对新技术的了解以及选用开发工具的使用熟练程度可以左右项目的实施情况。
4.2.3 确定 C 层各评价指标的权重
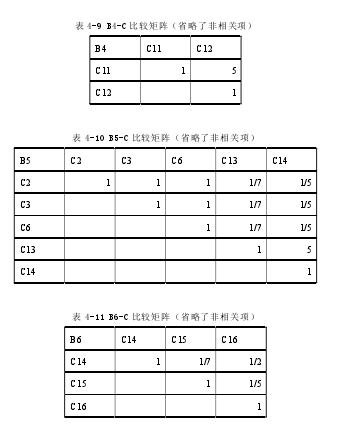
同样采用专家调查法,针对 B 层的每一个综合指标,在 C 层有相关性的评价指标间进行两两比较,获得关于每一个综合指标(B1--B4)的评价指标(C1--C16)两两比较矩阵 B1-C、B2-C、B3-C、B4-C、B5-C、B6-C(见表 4-6 到表 4-11 所示)。
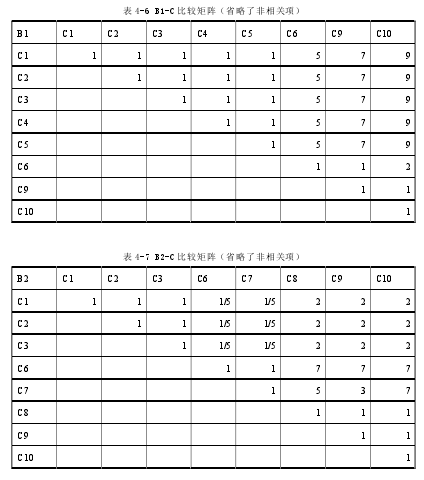
根据第 2.2 章节的公式及直接使用 Matlab 软件分别对上述 6 个比较矩阵计算得出其特征向量、最大特征根 maxl、一致性指标 CI、随机一致性比例 CR 等,并进行一致性检验:
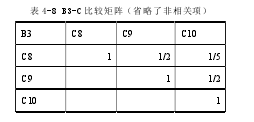
根据第 2.2 章节的公式及直接使用 Matlab 软件分别对上述 6 个比较矩阵计算得出其特征向量、最大特征根 maxl、一致性指标 CI、随机一致性比例 CR 等,并进行一致性检验:
W(B1) = [0.1833,0.1833,0.1833,0.1833,0.1833,0.0359,0.0267,0.0209] , maxl(1)=8.0224,CI(1)= 0.0032, CR(1)= 0.0023<0.1,通过一致性校验。
W(B2) = [0.0769,0.0769,0.0769,0.3348,0.3001,0.0438,0.0488,0.0418] , maxl(2)=8.1501,CI(2)= 0.0214, CR(2)= 0.0152<0.1,通过一致性校验。
W(B3) = [0.1283,0.2764,0.5953] , maxl(3)= 3.0055,CI(3)= 0.0028, CR(3)=0.0048<0.1,通过一致性校验。
W(B4) = [0.8333,0.1667] , maxl(4)=2,CI(4)=0,2 阶矩阵不需校验。
W(B5) = [0.0594,0.0594,0.0594,0.5820,0.2398] , maxl(5)= 5.2050,CI(5)= 0.0513,CR(5)= 0.0458<0.1,通过一致性校验。
W(B6) = [0.1125,0.3033,0.5842] , maxl(6)= 3.9814,CI(6)= 0.4907, CR(6)=0.8461<0.1,通过一致性校验。
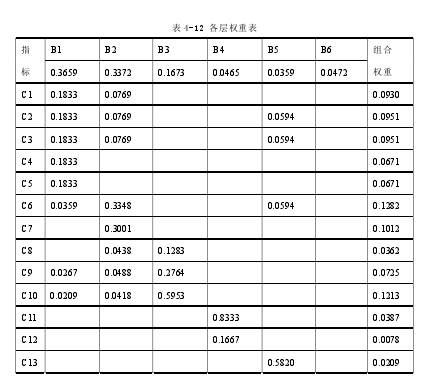
由上述 6 个特征向量补充对应的非相关项后组成矩阵 W(B),结合 B 层的综合指标的权重 W(A),计算 C 层各评价指标对于 A 层项目风险的组合权重 W=W(B) * W(A),计算得到W=[0.0930,0.0951,0.0951,0.0671,0.0671,0.1282,0.1012,0.0362,0.0725,0.1213,0.0387,0.0078,0.0209,0.0139,0.0143,0.0276] 。从而得到各层权重,见表 4-12 所示:
同样,需要对汇总后的矩阵作一致性检验,计算其一致性检验的如下指标:
==miiiCIbCI1,
==miiiRIbRI1,CR=CI/RI,其中 CIi 为与 bi 对应的 B 层的一致性指标,RIi 为与 bi 对应的 B 层的平均随机一致性检验的指标。
由上面的层次单排序知 CI1=0.0032, CI2= 0.0214, CI3= 0.0028, CI4=0, CI5=0.0513,CI6= 0.4907。通过平均随机一致性指标(表 2-4)可知 RI1=1.41,RI2=1.41,RI3=0.58,RI4=0,RI5=1.12,RI6=0.58。
经计算:CI=0.3660*0.0032+0.3372*0.0214+0.1673*0.0028+0.0465*0+0.0359*0.0513+0.0472*0.4907=0.0339;RI=0.3660*1.41+0.3372*1.41+0.1673*0.58+0.0465*0+0.0359*1.12+0.0472*0.58=1.1561;CR=0.0339/1.1561=0.0293,由于 CR 小于 0.1,所以结果具有很好的一致性。
最终得到 ZK 公司软件开发项目风险评估模型的评价指标体系,见表 4-13 所示:
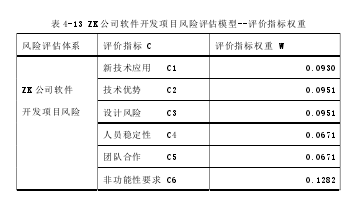
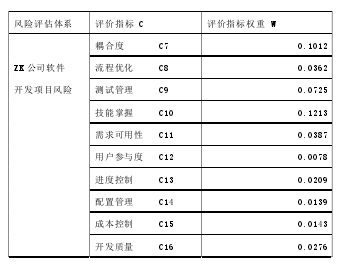
从该评价体系可以看到,非功能性要求 C6、技能掌握 C10、耦合度 C7、技术优势 C2、设计风险 C3、新技术应用 C1 等评价指标权重很高,这些指标可以直接影响软件开发项目的顺利进行,风险影响度很高。从这里可以看出,即使该评价指标的权重已经和综合指标的权重进行了组合,项目组微观操作层面认知的风险严重性和公司领导宏观管理层面是有些不同。当然,这也真正体现出 ZK 公司的软件开发项目管理特点,非功能性要求 C6 的风险系数更加反映出 ZK 公司的普遍客户群体(政府机关、事业单位为主),经常会提出额外的非功能性要求的实际情况,以致项目组技术人员对此心怀畏惧;而技能掌握 C10、耦合度 C7、技术优势 C2、设计风险 C3、新技术应用C1 确实是中小型软件开发项目最为重要的技术因素,在小团队里这些因素稍有不妥,将很快影响到项目的进度和质量。
4.2.4 定义评语集
根据 ZK 公司的日常管理习惯,对软件开发项目的风险程度划定为五个等级,评语集 V={V1(极低),V2(低),V3(一般),V4(高),V5(极高)}。
4.2.5 定义评价矩阵表格
根据表 4-3 以及上述定义的评语集,将两者组合则可以得出如下风险评价表格(见表 4-14)。
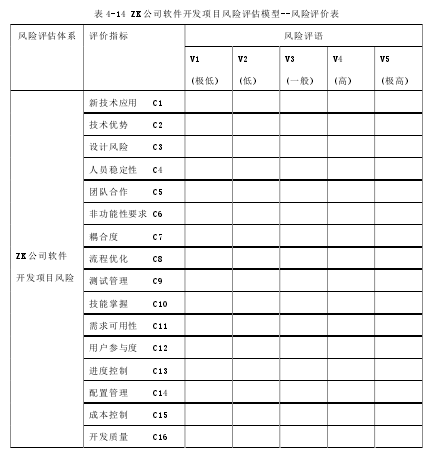
在需要对某一个进行中的项目进行风险评估时,运用专家调查法(参见章节 2.2.3),让项目组主要成员针对该项目对表内每一个评价指标给出唯一的一个评语,如该项目的需求到目前为止仍未完全清晰,风险较高,则对“需求可用性 C11”给出“V4(高)”的评价,在相应框中打钩即可。
4.2.6 模糊综合评价
在上一步骤得到所有评价参与者对项目当前状况的评价表后,以每个评价指标得到的评价比率作为隶属函数,每个评价指标对应的评语获得的打勾数除以参与评价的人数就是隶属度。显然,隶属度集是实数闭区间[0,1]。例如,参与评价的项目组成员有 5 人,对该项目利用表 4-14 进行风险评价,评价指标“新技术应用 C 1”一行中,有 2 人在“V2(低)”,3 人在“V3(中)”的评语打勾,评语“V2(低)”和“V3(中)”分别得到 0.4 和 0.6 的评价概率,其它 3 个评语的评价概率则为 0。评价指标“新技术应用 C 1”在对应评价集 V={V1(极低),V2(低),V3(一般),V4(高),V5(极高)},得到的隶属度分别是(0,0.4,0.6,0,0)。统计所有评价,从而很方便地得到该项目当前评价矩阵 R。
在得到具体项目的评价矩阵R后,结合上述用AHP方法计算得到评价指标权重W,根据 FCE 原理(参见章节 2.2.5)可以得到模糊综合评价向量 S = W * R,该模糊综合评价向量 S(S1,S2,S4,S4,S5)的各个值表示对应评语 V1(极低),V2(低),V3(一般),V4(高),V5(极高)的概率。
为了让本评估模型能够更加方便直观地给出评价结论,我们将主观评价的语义学标度进行量化,采取均匀分布的方式定义评语量化尺度,并依次赋值为1、2、3、4及5,主观测量用五级语义学标度。所设计的评价定量标准见表4-15。

最后,评估结果 v = S * E = (W * R) * E,评语量化尺度向量 E=[1,2,3,4,5] 。根据v 的数值直接得到评估对象的风险评语。根据上述隶属函数和隶属度的选择,评价矩阵R 的每一行都必然是归一的,评价指标权重 W 也是归一向量,所以最后评估结果 v 必然落在实数闭集[1,5]之内。当量化数值在[1,1.5]之间则属于风险“极低”,在(1.5,2.5]之间则属于风险“低”,如此类推。
4.3 ZK 公司软件开发项目风险评估模型
经过以上的模型构建过程,ZK 公司针对本公司的软件开发项目可以简单快捷地开展风险评估,核心内容是两份表格(表 4-13 有权重的评价指标表格、表 4-14 简单直观的风险评价表)和一个评估函数(v = (W * R) * E),具体的评估步骤如下:
1、以表 4-14 为样式,由具体软件开发项目组核心人员分别填写对该项目的风险评价表,统计各评价指标对应的评语比率形成对该项目风险的模糊评价矩阵 R。
2、计算 v=(W * R) * E,W 为表 4-13 的权重向量,E=[1,2,3,4,5] 。
3、根据 v 的数值对照表 4-15,得到该软件开发项目对应的风险定级和评语,V={V1(极低),V2(低),V3(一般),V4(高),V5(极高)}。





