
0、引言
光辐射是强爆炸的重要杀伤作用之一,通过对光辐射的定性分析,对于了解强爆炸的性质、评估其毁伤作用具有重要意义.早期有关光辐射的研究,建立在试验测量的基础上,结合相关的规律性分析,总结给出了光辐射功率走时的经验关系;在数值模拟方面,采用辐射流体力学方法,对光辐射功率进行了计算分析.在计算过程中,由于光辐射能流的强不稳定性(非线性、强烈依赖于物理参数等),因而通过一定的方法进行处理:一种是利用辐射热传导模型,辐射能流采用相应的扩散近似.
由于假设条件的苛刻,导致光辐射功率计算不够细致;另一种方法,对整个区域采用辐射流体力学方法直接求解,为避免辐射能流的剧烈振荡,对能流进行了平滑,这在一定程度上降低了辐射能流的计算精度,对于光辐射功率求解造成了困难.本文基于辐射流体力学计算方法,对光辐射输运过程采用直接求解.
为提高辐射能流的计算精度,并最大程度的提高计算效率,利用算子分裂方法将方程分裂为对流项和源项,二者独立求解,有效解决了光辐射计算中的辐射能流不稳定性问题,同时计算效率在原有基础上也得到了明显提升.给出的光辐射功率走时曲线,与已有结果和经验公式一致.
1、计算模型
强爆炸光辐射发展过程,是光辐射与流体耦合作用的过程,因而采用辐射流体力学方法,构建辐流耦合的物理模型.为简化方程求解,通常采用灰体近似方法,输运过程以矩方程形式给出.其中,辐射压强由最大熵Eddington因子方法确定:
流体力学方程组:

其中ρ为空气密度,u为空气速度,p为空气压强,e为空气总能量,κ′0为静止坐标系中考虑了受激发射的空气吸收系数;Er为辐射能密度,Fr为辐射能流,c为光速;φ=aT4为温度T下的黑体辐射能密度(a=5.67×10-16J/(m2·K4),为斯蒂芬-波尔兹曼常数).
最大熵Eddington因子下的辐射压强Pr=χEr:

空气的状态方程采用实际空气状态方程,即:

而eI、ρ分别为空气内能及密度.
通过以上方程组,在充分保证求解精度的基础上,能够完整、全面的反映强爆炸光辐射物理过程.
对于光辐射功率计算,取空气温度2000K为火球阵面,取计算得到的阵面处辐射能流,根据式(R为火球半径):
P=4πR2Fr(5)计算得到光辐射功率.
2、求解方法
采用算子分裂法的方案,将辐流方程组分为对流项和源项单独处理,原辐射流体力学方程组可化为如下形式:
对流项(式(6)第一项)通过有限体积法,构造五阶WENO格式,数值通量的计算采用局部Lax-Friedrichs方法,从而实现高精度求解.刚性源项(式(6)第二项)的处理,最终是化成了一个常微分方程组的求解问题.求解初始条件假定强爆炸总能量集中于等压火球内,辐射能与空气内能总合等于爆炸总能量,计算边界条件采用对称边界.
3、计算结果与分析
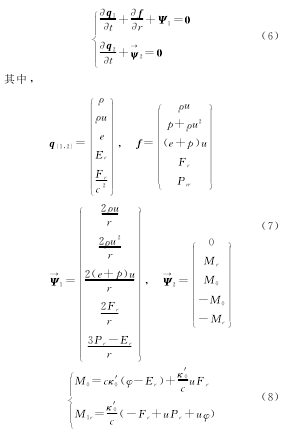
取当量为1kt、高度在海平面(h=0km),求解相应的强爆炸火球光辐射输运过程,空气初始状态参量如下:
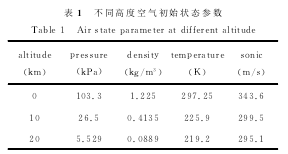
计算得到的强爆炸火球阵面走时(如图1)符合火球的物理过程,与Brode计算结果符合良好,证明了方法的可靠性.
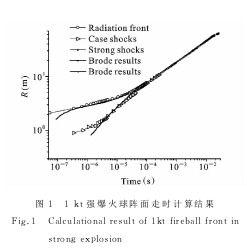
为研究强爆炸光辐射功率走时,需要先确定辐射能流随时空变化关系(式(5)).
图2、3分别给出了强爆炸光辐射不同时刻(4ms前后4ms后)辐射能流的时空分布.
从图中可以看出,辐射能流没有出现不稳定情况,同时时间步长较原有直接求解大为提高.光辐射能流在不同时刻的空间分布,有两个阶段:早期(4ms前),辐射能流随时间和空间位置向外单调减小,说明光辐射功率随爆炸能量向外发展逐渐减弱;在4ms以后,光辐射能流在空间分布上出现了逐渐增大过程,成为“双脉冲”.
光辐射能流的第二次脉冲,说明在后期阶段,强爆炸光辐射逐渐增大,与火球的“复燃”过程相对应.
辐射能流反映的是光辐射输运能量的大小,与空气吸收系数有着重要关系.
下图给出了4ms前后辐射能流与空气吸收系数、温度分布对比关系.
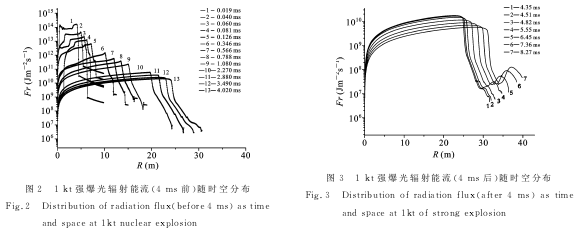

在t=2.88ms时刻,火球的辐射能流在空间分布为单脉冲,对应火球的温度均在10000K以上,而空气吸收系数也为单脉冲:辐射能流较大的位置,吸收很弱,而当吸收系数较大时,辐射能流开始减小;在t=8.27ms时刻,辐射能流在空间分布为双脉冲,在第二脉冲附近,火球温度已经降到几千K,此阶段,空气吸收系数在空间分布也出现了两个阶段:
第一阶段的分布与2.88ms基本一致,此后吸收系数在3000K附近,却出现了极小值,这也使得辐射能流出现第二次增大.
空气吸收系数再次极小的出现,与空气温度、密度有关,也是导致火球光辐射第二极大的根本原因.
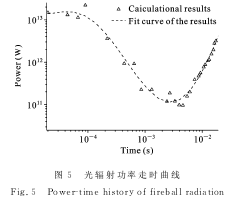
分析了辐射能流随时空分布及其与空气吸收系数的关系之后,利用式(5)给出光辐射功率走时关系(火球阵面为2000K,对应位置为火球半径):在计算的时间范围内,光辐射功率走时从开始逐渐减小,达到极小值后又开始增大,与实际火球发展过程一致.
其极小值对应于t=4.0ms,根据已有文献给出的结果,在1kt强爆条件下,光辐射功率极小值约为3.88ms,二者符合较好.
4、结论
采用辐射流体力学方法,直接求解了灰体近似下的强爆炸火球光辐射输运过程.利用算子分裂方法,实现对流项和强源项独立求解,保证了求解过程中辐射能流的稳定性,同时也极大提高了方程求解效率,在此基础上给出了1kt强爆条件下光辐射功率走时曲线.计算结果符合强爆火球发展过程,与已有结果一致.
参考文献:
[1] 屠琴芬.强爆炸火球的辐射流体力学计算中的几个问题[R].西安:西北核技术研究所,1986.
[2] 陈健华,王心正,谢龙生等.均匀大气中的强爆炸一维辐射流体力学数值解[J].爆炸与冲击,1981,1(2):37-49.
[3]Eugene M D Symbalisty,John Zinn,Rodnq W Whi-taker.Radflo Physics and Algorithms.LA-12988-MS.1995.
[4]Crowley K Barbara,David H Glenn,Marks E Robert.An analysis of marvel-a nuclear shock-tube experi-ment[J].Journal of Geophysical Research,1971,76(14):3356-3374.
[5]Marrs R E,Moss W C,Whitlock B.Thermal Radia-tion from Nuclear Detonations in Urban Environ-ments[R].UCRL-TR-231593,June 7,2007.
[6] 田宙,乔登江,郭永辉.不同高度强爆炸早期火球数值研究[J].兵工学报,2009,30(8):1078-1083.
[7] 高银军,田宙,刘峰等.基于多群方法的强爆炸早期火球数值模拟[J].应用物理,2011,2(2):163-167.
[8] 田宙,乔登江,郭永辉.不同当量强爆炸早期火球现象的数值模拟[J].爆炸与冲击,2009,29(4):408-412.
[9]Minerbo Gerald N.Maximum entropy eddington fac-tors[J].J.Quant.Spectrosc.Radiat.Transfer,1977,20(6):33-42.
[10]闫凯.二维辐射流体动力学方程组的数值求解.西北核技术研究所,硕士学位论文,2011.
[11]闫凯.二维辐射流体动力学方程组的数值求解.第六届全国青年计算物理学术会议,2011.
[12]乔登江.核爆炸物理概论[M].北京:国防工业出版社,2003.
[13]屠琴芬.高空强爆炸火球的一维辐射流体力学数值模拟[R].西安:西北核技术研究所,1987.
[14]屠琴芬.地下强爆炸早期火球的辐射流体力学总结[R].西安:西北核技术研究所,





