1、细绳水平转动状态
首先分析细绳水平转动状态：如图（1）所示，一条质量为M且分布均匀的绳子，长度为L，一段拴在转轴上，以恒定角速度在水平面上旋转。设转动过程中绳子始终伸直，且忽略重力与空气阻力，求距转轴为r处绳中的张力。
绳子在水平面内转动时，由于绳上各段转动速度不同，所以绳中各处的张力也不同。现取距转轴为r处的一小段绳子dr为研究对象，其质量为dm＝（M／L）dr，设左、右两边的绳子对它的拉力分别是T（r）与T（r＋dr）。这一小段绳子做圆周运动，根据牛顿第二定律，有：
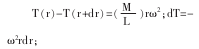
由于绳子的末端为自由端，即r＝L时，T＝0，所以：
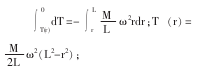
从以上结果看出，愈靠近转轴处绳中的张力愈大。
2、细绳竖直提起状态
再分析细绳竖直提起状态：长为l、总质量为m的柔软绳索盘放在水平台面上，用手将绳索的一端以恒定速率υ0向上提起如图（2），求当绳索上端离台面为x时手的提力。这是一个质点系运动的问题，可用质心运动定理来分析。取x轴垂直向上，以台面为原点，则当绳索提起x长时，系统的质心坐标为
可见提取细绳的力F随速度υ0增大而增大，随高度增加而增大。类似情况还有：长为l、质量M均匀分布的柔绳，一端挂天花板下的钩子上，将另一端缓慢地垂直提起，并挂在在同一钩子上，试通过直接积分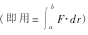
可以求出该过程中对绳子所作的功。
这是一个变力作功问题，取绳自由下垂时末端位置为坐标原点，铅直向上为Ox轴正向，如图3，当可见该过程对绳子作的功与绳长有关。
3、细绳静止下落状态
下面再来讨论细绳静止下落状态：一质量为m，长为l的完全柔软均匀细绳竖直地悬挂着，其下端刚刚与地面接触如图4。放开绳子，使之从静止状态开始下落。求在下落过程中地面对绳的作用力。
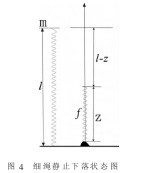
以地面为坐标原点建立竖直向上的z轴。把绳子看做一质点系，其质心高度和速度分别为
由此可得质心加速度为：
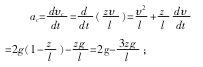
设地板对绳子的作用力为F，对整根绳子应用质心运动定理，有：F－mg＝mac；将ac的表达式代入上式，得地板对绳子的作用力为：F=m（g+ac）=3mg（1-z／l），可见作用力与绳长下落的长度有关，类似情况还有：
一质量为m、总长为l的细绳，开始时有一半放在光滑的桌面上，而另一半下垂，如图（5）所示，试求细绳桌面边缘时重力所作的功。
重力所作的功，等于细绳势能增量的负值，取桌面为势能零点，因而有：
如：一根质量为M、长度为L的细绳、被竖直地悬挂起来，其最低端刚好与秤盘接触．今将细绳释放并让它落到秤盘上，如图（6）所示．当细绳下落的长度为x时，试求秤的读数是多少？
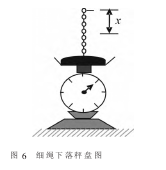
秤的读数反映了细绳对秤盘的作用力的大小，数值上也等于秤盘对细绳作用力的大小。该力由两部分组成，第一部分为已落入盘中的细绳所受的力F1，其数值等于其重力，取竖直向上为坐标轴正向：
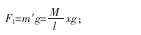
第二部分为正要落入盘中的部分作用力F2，设其质量为Δm′，根据动量定理，此时忽略其重力，
综上各种情况：细绳可看成多质点构成质点系，通过张力作用。
在各种状态下，机械能不守恒，但通过相关物理规律可以了解在不同状态下存在各种变化规律，反映其内在力学特性。
参考文献：
1．马文蔚．物理学（第四版）［M］．北京：北京高等教育出版社，1999
2．周衍柏．理论力学（第二版）［M］．北京：北京高等教育出版社，1986
3．朱照宣．理论力学［M］．北京：北京大学出版社，1982
4．李承祖，杨丽佳．基础物理学（上册）［M］．北京：北京科学出版社，2004
5．王少杰，顾牡．大学物理学第三版（上册）［M］．上海：上海同济大学出版社，2006
