
一、引 言
资产价格与宏观经济变量之间的作用机制与效果是经济学研究中最受关注的领域之一,2007 年发生的全球性金融危机使中央银行是否应该“事后清理”———当资产价格泡沫破裂或价格快速下降时进行政策干预,减轻对宏观经济的冲击,还是“逆风而动”———当资产价格泡沫形成或资产价格不断上升时适时调整,成为争论最为激烈的问题之一。
持前一种观点的学者认为资产价格对宏观经济的影响较小,所以中央银行应该仅对通货膨胀及( 或)失业率进行积极的干预,对资产价格波动只需关注而不必将其作为中介目标,即便资产价格中出现明确的泡沫成分。
①后一种观点认为资产价格波动对宏观经济的影响较大,并认为,也许经济运行平稳时资产价格对宏观经济影响较小,但在宏观经济运行异常时却可能较大,甚至不同经济状态下的影响效果可能完全相反; 此外,资产价格波动可能影响宏观经济发生异常状况的风险。这对于如同“风险管理专家”一样操持货币政策的中央银行而言更为重要。
两种观点的争议核心在于资产价格对宏观经济的影响效果上。不同的研究对象和样本下的实证分析结果常常存在较大的差异; 此外,关注于被解释变量的均值或分布的不同分位等研究方法的不同也是形成认识上差异的重要原因。尽管如此,学术界的反应似乎相对缓慢( Cecchetti,2008),多数研究依然在均值回归的视角中洞察资产价格对宏观经济的影响,仅有 Cecchetti( 2008)、Gochoco-Bautista( 2008)等少数研究摆脱传统的框架,在资产价格对宏观经济变量的尾部影响的研究上迈出重要的、探索性的一步。
本文采用分位数回归方法,比较分析我国股票价格波动对宏观经济变量———产出缺口与通货膨胀的左、右尾部及均值的影响,以期探究在不同经济状况下资产价格对宏观经济的影响,为央行制定货币政策提供研究依据。分析结果表明股票价格对产出缺口和通货膨胀的均值影响均不显着,但对尾部的影响效果却较为显着,且对左右尾部的影响是非对称的。
二、相关理论及文献
( 一) 传统理论
对资产价格( 及资产收益) 与宏观经济之间关系的研究由来已久,资产价格变动对产出的影响机制主要包括财富效应、投资效应等。财富效应认为,资产价格上升使消费者的财富增加资源约束减弱,进而再扩大消费需求; 投资效应或托宾 Q 理论从投资者角度分析资产价格对产出的影响,当资产价格( 即市值)上升高于其投资成本时,投资变得更为有利可图,因而增加投资需求。近年来,信贷约束理论和金融加速器等金融摩擦理论为资产价格与投资提供了新的解释。信贷约束理论认为资产价格上升意味着抵押品价值增加,信贷约束减弱,企业可以为更多的可投资项目融资,投资也会增加。金融加速器理论与信贷约束理论相似,认为资产价格上升能缓解信贷约束,降低融资成本,进而使投资增加。此外,资产价格也可能通过影响消费者( 或投资者) 的信心进而影响宏观经济( 信号作用) 。资产价格( 现值) 等价于未来预期收益的贴现和,资产价格的变化反映投资者对未来经济的预期,所以资产价格下跌会通过预期进而影响消费、投资行为。例如,股票价格下跌,人们以此推断未来经济可能会出现滑坡,进而减少现期消费。
与资产价格—产出关系相比,对资产价格与通货膨胀的研究更为久远,成果更为丰富。资产是对其代表的实物资本的索取权,因实物资本的价值不受通货膨胀的影响,所以证券资产被认为是一种抵御通货膨胀( 对冲通货膨胀风险) 的有效工具之一。Fisher 假说认为,名义利率应该等于预期通货膨胀率加上实际利率。保值假说认为资产代表着对实物资本的索取权,实物资本的价值不受通货膨胀的影响,具有保值的功能,所以当通货膨胀上升时,至少在长期里投资者基于对冲通货膨胀风险财富保值的目的会增加对实物资产的需求,进而使资产价格上升。
随着理论的发展,学者们对资产价格与宏观经济之间的关系做了大量的实证研究,然而对二战后美国等国家的实证分析结果却显示通货膨胀率与实际股票收益呈反方向变化。因此,一些学者提出了新的假说,以解释实际股票收益与通货膨胀之间反向变化的现象。
Modigliani 和 Cohn ( 1979)的通货膨胀幻觉假说认为,股票投资存在通货膨胀幻觉( 通货膨胀发生时,误认为股票收益增加,进而增加投资,导致收益减少) 。当通货膨胀上升时,股票投资者倾向于加大对未来收益和分红的折现率( 高于名义利率) ,从而出现股票价格被低估的现象; 同理,通货膨胀率下降时股票价格会被高估。Fama 假说认为实际资产收益与实际经济活动呈正相关,而通货膨胀与实际经济负相关( 依据货币需求模型) ,所以股票价格与通货膨胀预期呈( 虚假) 负相关。Brandt 和 Wang( 2003)时变风险规避假说认为,通货膨胀使投资者变得更倾向于风险规避,因此推高了风险溢价和实际折现率。除此之外 Feldstein( 1980)、Geske 和 Roll( 1983)、Hess 和 Lee ( 1999)等也从不同角度对此现象做出了解释。
①Schwert ( 1989)等对美国资产价格波动与宏观经济变量的实证分析表明资产价格对宏观经济波动有着重要影响。Lee ( 1992)采用 VAR 方法分析了二战后美国资产收益与实际宏观经济变量之间的关系,发现股票收益对未来实际经济活动的影响较显着,但对通货膨胀率的影响较小。Aylward 和 Glen( 2000)对 1951 ~1993 年间的 23 个国家( 其中 15 个发展中国家) 进行了实证分析,发现各国股票价格对未来的实际经济影响显着,而且 G7 工业国的股票价格对其经济的影响明显强于发展中国家。Aylward和 Glen ( 2000)的结论符合一般性的经济直觉———在发达国家,金融系统比较完善,资产价格与宏观经济之间的联系更加紧密,相互作用也必然更为显着。
( 二) 最新发展
不断出现的金融危机促使一些学者从更宽的视角分析资产价格对宏观经济的影响,为什么在平稳的宏观经济状况下突然发生金融危机? Cecchetti ( 2008),Gochoco-Bautista ( 2008)等学者将研究的焦点置于资产价格对产出及通货膨胀尾部的影响。Cecchetti ( 2008)实证检验 17 个工业化国家的资产价格( 证券和房地产) 快速上升对产出和通货膨胀出现异常情况的边际影响———即对其概率分布的左、右尾部的影响。结论认为房地产泡沫改变宏观变量的整个分布,而证券价格虽然几乎不改变宏观经济变量的均值和方差,但会使恶劣的情况变得更加恶劣。Gochoco-Bautista ( 2008)采用相似的方法分析东亚 8 国资产价格对宏观经济的影响,认为资产价格对宏观经济的影响是非对称的,资产价格泡沫仅使恶性结果的发生概率增加,但不会增加良性结果出现的概率。
Cecchetti ( 2008)和 Gochoco-Bautista ( 2008)的研究结果不仅对普遍运用着的简单货币政策法则提出质疑,也为重新认识资产价格对宏观经济的影响提供了重要启示———仅关注资产价格对宏观经济变量均值的影响是不够的。
( 三) 国内相关研究
国内学者对我国资产价格对宏观经济的影响也做了大量的研究。王虎、王宇伟、范从来( 2008)采用 VAR 模型分析了 1997 ~2006 年我国股票价格、价格水平与产出之间的作用效果,结果表明股票价格对滞后一年的 CPI 有正影响,而且影响比较稳定,对产出缺口虽有正影响但不稳定,认为财富效应和投资效应都不明显。Peng、Cui 和 Qin ( 2009)采用 4 阶滞后的 VECM 模型分析了我国股票价格对宏观经济的影响,结果表明资产价格不是产出的格兰杰原因,但产出是资产价格的格兰杰原因。Wang ( 2010)等的研究结果却与 Peng、Cui 和 Qin ( 2009)、王虎等( 2008)的结论颇有差异。Wang ( 2010)采用EGARCH 模型对 1992 ~ 2008 年中国股票价格波动与宏观经济变量波动进行了格兰杰检验,发现股票价格波动与 GDP 波动各自独立变化,相互不为格兰杰因果关系; 与 CPI 则存在双向的因果关系,认为股票价格上涨引发消费增加,进而引起价格上升。这样的结果留下了一个疑问,如果股票价格变化与价格水平之间的中间环节是消费,那么股票价格与产出应具有格兰杰因果关系,而不是互不存在因果。
由上述文献回顾可见,多数先行研究主要采用( S) VAR,Granger-Cause 等均值回归的方法,结论为宏观经济变量的均值对资产价格变化的响应,即在“正常经济状态”下的影响,对审慎地制定宏观政策的央行提供有限的参考依据。为此,本文采用分位数回归方法探索股票价格波动对宏观经济的影响,具体地,本研究重点分析股票价格波动对产出缺口和通货膨胀分布的左尾部( 0. 05 分位) 和右尾部( 0. 95 分位) 的影响,对应的经济含义分别可理解为经济过热、萧条时股票价格波动对产出的影响,以及高通货膨胀、高通货紧缩时股票价格波动对通货膨胀的影响。
三、模型与实证方法
( 一) 实证模型设计
基于简练原则和本文的研究目的,假定当期的产出缺口与通货膨胀的动态过程受自身及股票价格滞后期的影响。这样的设定不仅符合宏观经济变量变化过程中的惯性特征,也可以消除实证中误差项自相关问题。另外,为避免股票价格自身动态过程对结果产生异常影响,实证研究中仅采用某一滞后期的股票价格作为解释变量,作为这一设定的弥补,采用不同滞后期的股票价格作为待选。以 Cecchetti ( 2008)和 Gochoco-Bautista ( 2008)的研究思想为基础,本文将实证模型设定如下:【1】
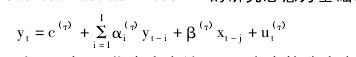
式( 1) 中,yt代表产出缺口( 下文中简称产出) 或通货膨胀,xt - j代表股票价格缺口,下标 i 表示被解释变量( 产出或通胀) 的自回归阶数,下标 j 代表解释变量———股票价格缺口的滞后阶数。待估参数 c( τ),α( τ)i,β( τ)的上标 τ 表示分位数,因此参数 β( τ)则表示对被解释变量 τ 分位的影响。除上式( 1) 外,作为辅助的稳健性分析,也将估计仅有股票价格单一解释变量( 不含解释变量自回归项) 的回归方程。这样的设定可以最大程度地减少主观设定对分析结果的影响。
( 二) 分位数回归方法
基于 OLS 或 MLE 的均值回归关注的是被解释变量的条件均值对解释变量的响应程度,隐含地假定解释变量对被解释变量各分位的影响是均匀的,以本文为例,意味着在不同经济状况下( 萧条或高胀) 股票价格对宏观经济变量的影响是相同的,显然这与经验证据不符。Konener 和 Bassett ( 1978)提出的分位数回归方法可以估计解释变量与被解释变量不同位之间的线性影响效果。借助各分位参数估计值可以观察解释变量对被解释变量各分位的边际效应。【2-3】

假定残差项的条件期望值为 0,即 Qτ( u|ξ) =0,则被解释变量 τ 分位条件值 Qτ( Y|X = x) 等于系数估计值与解释变量的乘积,因此系数 Θ( τ)表示相应解释变量对被解释变量 τ 分位的影响。τ 分位回归参数估计值 Θ^( τ)则通过优化下式求得:【4】
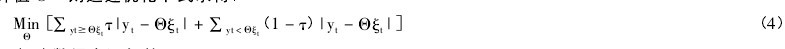
( 三) 数据来源与整理
本文实证分析中所用数据为 1992 年第一季度 ~ 2013 年第三季度共 87 个季度样本。采用对数实际GDP、对数上证综指( SSE) 在 HP 滤波( Hodrick-Prescott) 下的波动部分代表产出缺口和股票价格缺口,采用消费者价格指数( CPI) 的增长率表示通货膨胀。各序列均为季度调整后数据,所有原始数据取自《锐思数据库》。
四、实证分析结果
( 一) 股票价格缺口对产出缺口的影响
不同设定下股票价格缺口对产出缺口的均值、0. 05 分位及 0. 95 分位的影响见表 1。表中的列表示模型设定方式,行向的第一部分为均值回归下的参数估计值,第二部分为位数回归下 0. 05 分位、0. 95 分位的系数估计值( 下同) 。
由均值回归结果可见,当滞后一期的产出缺口作为解释变量时,误差项自相关现象基本消失,以此为基础分别引入滞后 1、2、3 期的股票价格缺口作为解释变量。均值回归时,所有的系数估计值在统计上都不显着( 见表 1 中模型 1、模型 2、模型 3 列的估计结果) 。考虑可能存在产出缺口的滞后变量与股票价格缺口之间可能存在多重共线性,故仅用股票价格缺口的滞后变量作为唯一的解释变量进行均值回归,然而系数估计值仍然在统计上不显着,回归方程的拟合度也没有明显的改变。这样的结果与先行研究中“股票价格缺口对产出的影响并不显着”的研究结论基本相似。
虽然股票价格对产出均值的影响不显着,但对左、右尾部的影响却比较显着。对产出 0. 05 分位的回归结果见表 1( 表 1 的中间部分) 。首先,滞后 1 期产出缺口对当期产出缺口的影响在统计上不显着,表明在经济萧条时产出缺口的持续性并不明显; 其次,无论是单独抑或与滞后产出缺口共同作为解释变量,滞后 1 期和 3 期的股票价格缺口作为解释变量时,相应系数估计值在统计上显着( 在 0. 1 和 0. 01 显着性水平) ,影响方向为正,说明当经济萧条时股票价格上升引起产出增加。
对产出0. 95 分位的回归结果与0. 05 分位的结果截然不同( 见表1 的第三部分) 。滞后1 期产出缺口的系数估计值在统计上是显着的,说明在经济繁荣时产出缺口的惯性比较明显。然而,除滞后 3 期的股票价格作为独立的解释变量之外( 模型 6) ,股票价格缺口对产出缺口的影响均不显着。
股票价格仅在经济萧条时产出缺口影响较为显着的原因在于: 当经济繁荣甚至过热时,市场对投资的未来回报较为乐观,所以投资约束较弱,股票价格上升对投资及产出的影响甚微; 反之,当经济萧条时,市场对投资收益较为悲观,投资约束较强,投资者融资约束较强,所以股票价格( 抵押品价值) 上升对投资者融资产生较大帮助。从信贷周期理论而言,银行行为是“后顾型”,即依据过去的信息进行决策。当经济繁荣企业投资收益好时,银行甚至可能会提供信用贷款,而在经济萧条投资收益较差( 或违约概率较大)时银行对抵押贷款的要求更严格。【表1略】
( 二) 股票价格缺口对通货膨胀的影响
股票价格缺口对通货膨胀的均值及分位数回归下的参数估计值见表 2。【表2略】
均值回归结果表明,滞后通货膨胀率的参数估计在统计上显着,均衡影响( 即滞后期的系数之和) 均大于 0. 8,表明通货膨胀具有很强的惯性。然而所有设定下,股票缺口对通货膨胀均值的影响均不显着,也没有明确改善回归的拟合度。与均值回归相比,分位数回归结果更引人关注。
与均值回归相比,在 0. 05、0. 95 分位上通货膨胀的惯性虽然依然显着,但出现较大的分化。在 0. 05分位上通货膨胀滞后期的系数之和约为 0. 56 ~0. 72,而在 0. 95 分位上系数之和均大于 0. 9,说明在高通货膨胀时期惯性极强,而在严重通货紧缩时惯性略小些。依据新凯恩斯理论,可能的解释是当通货膨胀率较高时,企业对此做出过度反应,定价时更依赖于“经验法则”。
虽然股票价格对通货膨胀均值的影响不显着,但对其 0. 05、0. 95 分位的影响却不然。在低分位( 0. 05分位) ,存在自回归项时,仅滞后 4 期的股票价格缺口的系数估计值在统计上显着; 不存在自回归项时,滞后 3 期、4 期的股票价格缺口对产出缺口的影响都在统计上显着,而滞后 1、2 期的股票价格缺口的系数估计值仍不显着,在统计上显着的系数估计值均为负值。说明在严重通货紧缩时,股票价格缺口对通货膨胀的作用时间比较长,影响为负,即股票价格缺口增加时通货膨胀率变小。股票价格缺口对通货膨胀 0. 95分位的影响表明( 见表 2 的第三部分) ,存在自回归项时滞后 1 期和滞后 4 期的股票价格缺口的系数估计值在统计上显着,不存在自回归项时滞后 2 期、3 期、4 期的股票价格缺口的系数估计值在统计上显着,统计上显着的系数估计值均为正。此外,0. 95 分位的参数估计值均明显大于相应的 0. 05 分位的估计值。
货币主义理论为高通货膨胀时股票价格上升使通货膨胀加剧,而严重通货紧缩时使通货紧缩更加严重的现象提供了一种可能的解释。假定高通货膨胀时期货币增长率较高,而在严重通货紧缩时货币增长率较低,股票价格缺口增加导致货币需求增加,当通货紧缩时会导致价格下降,而在通货膨胀较高时则相反,使价格上升。
五、结 论
本文采用 1992 ~2013 年时间序列分析了资产价格对产出缺口和通货膨胀左、右尾部的影响。实证分析结果表明,股票价格缺口仅对产出缺口的低分位影响比较明显,且影响方向为正,即在经济萧条时股票价格上升使产出增加。而股票价格对通货膨胀的影响则为双侧非对称影响,即在严重的通货紧缩时股票价格上升使通货紧缩加剧,而在高通货膨胀时,股票价格缺口也会使通货膨胀加剧。从影响强度上看,股票价格缺口在高通货膨胀时的影响强度明显大于通货紧缩时期。
依据本文的实证结果,提出如下政策建议: 当宏观经济处于相对平稳状态时,即产出和通货膨胀都比较温和时,中央银行可以不将股票价格纳入调控范围。但是当宏观经济出现异常时,特别是通货膨胀率过高或过低时,须密切关注股票等资产价格,适时对其进行政策干预。





