
0 引言
居民消费价格指数,简称为CPI,它是反映城乡居民家庭购买并用于日常生活消费的一篮子商品和服务项目价格水平随时间变化的相对数,是重要的经济预警指标,称之为经济发展的晴雨表,既可度量通货膨胀(通货紧缩)的严重程度,又可用于国民经济核算和指数化,如工资、租金、利息或税收之类的货币流量的调整,各级政府通过它来了解全国各地价格变动的基本情况,分析研究价格变动对经济社会和居民生活的影响,从而制定相应的宏观政策和计划、进行宏观调控。
随着经济的发展和市场化程度的不断深入,人们对CPI的关注度越来越高,政府部门的政策制定者、企业家管理者以及金融投资者均高度关注着CPI的发展趋势,想以此来制定政策或进行投资规划,为此,很多学者围绕CPI的准确预测和度量进行了大量的理论和实证研究。由于CPI具有明显的季节因素,因此不管何种预测方法,如何进行CPI季节调整极为关键。目前,对CPI季节调整的研究主要是有两方面,一是用X-12-ARIMA或其改良方法来探测交易日、闰年、异常值和春节对CPI的影响;二是运用 CPI 的同比指数、环比指数或者二者结合来对建立SARIMA模型并进行短期预测。相对于单一的对同比和环比序列建模而言,结合两种模型构造的合成预测值的预测精度更高。
用定基比来建立SARIMA模型并进行预测的文章并不多见,在桂文林的中国居民消费价格指数间的关系与选择中,研究了环比、同比和定基价格指数以及环比“折年率”之间的相互转化情况,并验证了研究中同比向定基比转化的合理性。由此,本文利用CPI定基价格指数,应用SARIMA模型,构建定基比CPI预测模型,并对预测精度进行分析。
1 CPI同比、环比、定基比的比较
在国家统计局网站上,目前主要公布的是以上年同期或上年同月为基期的同比指数,即报告期某期或某月消费者物价水平与上年同期或同月消费者物价水平相对比的一种相对数,这种同比指数所反映的是某期或某月相距12个月的物价变动情况,且对比基期又在不断变化波动,受到基期价格波动的影响,无法准确地反映出近期物价的波动,对价格变动反映不够灵敏,再加上在存在“尾因素”,因此在实践中存在一些缺陷。
在反映经济时间序列的变动情况时,同比反映变动的转折点慢于环比,不利于及时把握拐点和变动趋势。因此,为了提高统计数据的及时性,有必要进行环比指数的计算。环比价格指数指在一个价格指数数列中,每个指数都以计算期的前期为基期(对比期)而计算的价格指数。
其特点是基期随计算期的变动而有规律的变动。常用的月环比价格指数,就是以上月价格水平为100的价格指数。月度环比指数反映了一个较短时期内(一个月)的价格变动,由于时间较短,老百姓印象更深刻,感受更强烈。
分析短期变化一般采用环比数据,但环比价格指数受季节、气候和突发事件的影响较大。
定基价格指数是指在一定时期内对比基期固定不变的价格指数。通常以某一年为基期来计算。以固定期价格水平为100,如果计算期的价格指数高于100,表示这一时期的价格水平上升,低于100,则表明这一时期的价格水平下降。编制定基价格指数的目的在于观察物价变动长期趋势及其规律。这是世界上多数国家计算居民消费价格指数所采用的方法。
从月同比、月环比、定基价格指数间的相互转化来看,桂文林的中国居民消费价格指数间的关系与选择,有三者之间的定义公式可以看出,由定基指数可以准确地计算同比和环比价格指数,也可以从环比指数到同比指数转换,但无法从同比指数到环比指数或定基指数的转换,可见,定基指数是转化能力最强的指数,环比指数次之,同比价格指数的转化能力最弱。
从定基价格指数的作用来看,主要有三方面:
一是能够剔除数量结构变化对月度或季度环比价格指数的影响,单纯反映月度或季度市场价格的变化趋势,从而加强对短期价格变动的影响分析、走势判断和宏观监测。
二是可以观测任意时期价格变动状况,大大提高价格统计指标的应用价值。由于定基指数分月计算针对固定基期的价格变动幅度,它既可以观测较长时间(如5年),也可以观测较短时间(季度累计、月份)价格变动情况,适应性和实用性都很强。
三是有利于价格统计资料的国际对比,实现价格统计制度方法与国际接轨。
2 时间序列SARIMA模型
2.1 季节调整的蕴含
季节因素调整是现代统计学的缩影,它是以现代数理统计模型为基础,通过模型识别、参数估计和模型的检验、预测应用多阶段的计算,剔除掉原始数据中的季节因素和偶然因素,在面临非常复杂的数据库时,运用计算机这一工具在短时间内把多而杂的枯燥数据变成清晰可视的曲线图,从而提高了数据的分析和使用价值,使人们更加清楚地看到并掌握在某一时刻所要了解的经济发展的趋势。
2.2 SARIMA模型简介
SARIMA模型来源于自回归单整移动平均模型(ARI-MA),ARIMA模型由博克斯(Box)和詹金斯(Jenkin)创立,亦称B-J方法,它是一种精度较高的时序短期预测方法,能够更加本质地认识到时间序列的结构与特征,达到方差意义下的最优预测。针对季节时间序列Xt的方法是,首先对作各种不同的差分变化,然后再分析经变换后的序列的偏相关函数(EACF)。一般来说,总是反复对序列做差分运算,直到EACF表现出某类易于解释的特征,即其中有少量的相关系数显着时为止。由该种方法最后所确认的ARIMA模型,由于通常包含周期性滞后期的有关参数,因此就常常被称为季节ARIMA模型,即SARIMA模型。
季节时间序列模型即SARIMA(p,d,q)(P,D,Q)s模型一般表达式为:
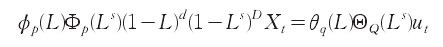
式中,P是季节自回归阶数,Q是季节移动平均阶数,s为周期,并且分别称ΦP(Ls)和ΘQ(Ls)为季节P阶自回归算子和Q阶移动平均算子。ut为均值为0. 方差为σ2的正态分布,并且对任意的k,有cov(et,et-k)=0.
当P=D=Q=0时,SARIMA 模型退化为 ARIMA 模型;当P=D=Q=p=q=d=0时,SARIMA模型退化为白噪声模型。
3 定基CPI指数预测模型的构建与实证分析
3.1 定基CPI的数据特征
数据采样区间为居民消费价格指数(CPI)1990.1~2012.11上年同月为基期的同比指数数据,数据来源于国家统计局网站和中经网数据库,以1990年为基期,进行定基计算,选择1990.1~2012.11定基共275个样本数据,为了检验模型向后预测的准确度,在进行模型的构建时,2012年1~11月的数据没有参与模型的构建和参数估计,只用作模型精度的评价,因此实际参与模型构建的样本数据为264个。
3.1.1 平稳性检验
将 1990.1~2011.12 CPI 月度定基指数序列记为Xt序列。由图1知,CPI定基指数Xt序列递增型呈现周期性变化,我们可以根据经验初步看到Xt序列是不平稳的,存在着季节性。采用 ADF 检验序列平稳性,如表 1 可知,在1%、5%和10%的显着性水平下,τ=-2.142698>τα,不能拒绝存在单位根的原假设,即Xt序列是非平稳的序列。
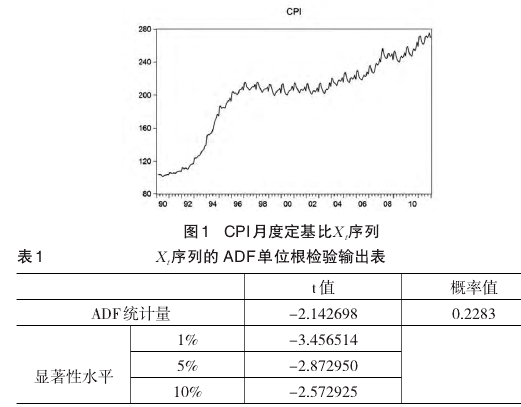
3.1.2 季节性检验
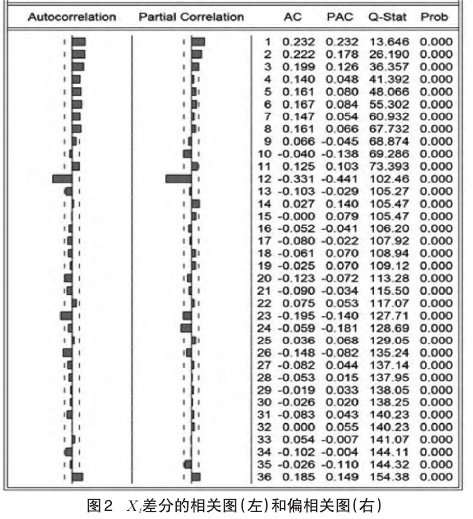
从图1可以看出Xt序列存在周期性的季节波动,为了更进一步证明定基CPI的季节性特点,我们借助时间序列的样本自相关函数来检验时间序列中的季节性特点。如果一个时间序列数据中有季节性,那么通常它的自相关系数也具有相应的季节性特征,由于Xt序列是一个非平稳序列,对其进行一阶差分,消除长期趋势后,其差分序列的自相关分析图(图2)可知,r12=-0.331,r24=-0.059外,自相关系数基本都落入随机区间内,说明定基CPI具有较强的季节特点。
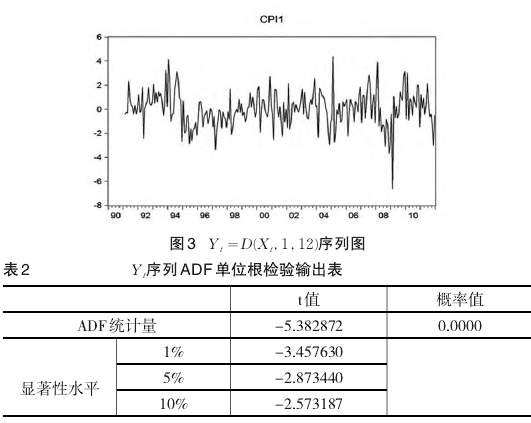
3.2 SARIMA预测模型的构建CPI月度定基比序列是具有季节特点的非平稳序列,且存在12期滞后,因此,序列模型可考虑包含长期趋势,季节调整且能够拟合CPI定基的随机波动。本文选取带季节ARIMA模型即SARIMA模型。
对Xt序列进行一阶十二步差分得到Yt=D(Xt,1,12)后,画出序列图,如图3,可初步判断该序列是平稳的,用ADF检验来进行判断,其检验结果见表2,在1%的显着性水平下,检验结果拒绝原假设,接受原假设存在单位根,从而确定Yt序列为平稳非白噪声序列。
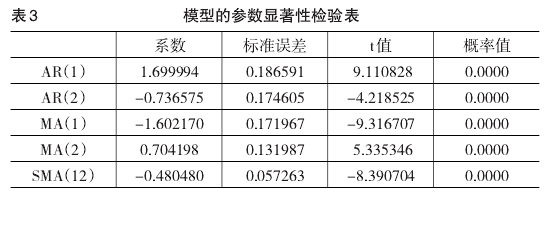
根据它的自相关系数和偏自相关系数的特征,我们建立乘积模型SARIMA(2,1,2)×(0,1,1)12,利用最小二乘法(ls)估计参数,如表3,模型中的参数检验都是显着的,通过对残差序列进行Q检验,残差序列为白噪声序列,说明此模型是比较理想的。最终,我们得到的模型如下:
(1-1.699994L+0.736575L2)(1-L)(1-L12)Xt=(1-1.602170L+0.704198L2)(1-0.480480L12)ut.
模型中的参数显着性检验结果如表3:
4 结论
对历史数据拟合程度的高模型并不完全代表对未来预测的准确度,为了证明模型进行外推预测的准确性,本文在构建模型时将2012年以后的数据不参与参数的估计,只用来对模型预测精度的评价,避免样本内外预测精度不一致的缺陷,同时向后即2012.12~2013.2做预测,分析CPI的未来走势。在处理数据时,我们把预测的CPI定基指数转化为CPI上年同月为基期的同比数据。
4.1 精度评价
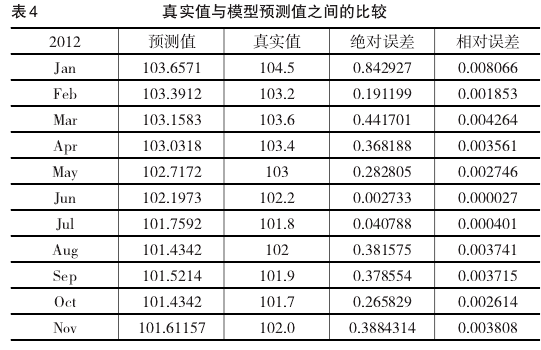
我们利用该模型对2012.1~2012.11的CPI定基指数进行预测,然后通过计算转化为CPI上年同月为基期的同比指数,与国家统计局公布的上年同月为基期的同比指数即真实值相比较,真实值和预测值之间的比较见下表4,结果表明模型的相对误差均在1%以内,可见预测精度很高。
4.2 CPI后期走势分析
通过该模型,对2012.12 -2013.2 CPI定基指数进行预测,然后通过计算转化为CPI上年同月为基期的同比指数,同国家统计局公布的数据一样也保留一位有效数字,得出,2012年12月CPI为101.7,2013年1月CPI为100.8,2013年2月CPI为101.8.
参考文献:
[1]中国人民银行调查统计司.时间序列X-12-ARIMA季节调整-原理与方法[M].北京:中国金融出版社,2006.
[2]易丹辉.数据分析与Eviews应用[M].北京:中国人民大学出版社,2008.
[3]张虎.季节调整方法在CPI指数中的应用[J].统计与决策,2011,(2)。
[4]张鸣芳.居民消费价格指数季节调整实证研究[J].财经研究,2004,30(3)。
[5]栾惠德.季节调整中的春节模型[J].经济学(季刊),2007,6(2)。
[6]贺凤羊,刘建平.如何对中国CPI进行季节调整[J].数量经济技术研究,2011,(5)。
[7]张健.SARIMA模型在预测中国CPI中的应用[J].统计与决策,2011,(5)。
[8]桂文林,韩兆洲.中国居民消费价格指数间的关系与选择[J].
统计研究,2012,29(9)。





