本篇论文目录导航:
【题目】国内生物制药行业经营状况评估
【第一章】中国生物制药业发展现状探究绪论
【第二章】数据包络模型与Malmquist生产率指数
【第三章】DEA模型指标的设定及数据来源
【第四章】我国生物制药行业绩效的实证分析
【结论/参考文献】生物制药行业健康发展研究结论与参考文献
第2章 研究的理论和模型综述
2.1 数据包络模型(DEA)
2.1.1 数据包络理论
效率的测量已成为能引起奋力改进生产力机构极大兴趣的主题。50 年前,法雷尔(1957)关于生产力效率的经典论文给出了最好的陈述。
"关于测量一个产业的生产力效率问题对于经济理论家和经济政策制定者都非常重要。如果以不同经济体制的相对效率的理论依据是受到实证检验,那么必不可少可以得出一些效率实际测量值。同样,如果经济规划所关心的是自身在特定产业的情况,那么获知在没有吸收更多的资源条件下,期望特定的产业增加其输出量仅通过提高其效率能达到什么程度。"法雷尔进一步指出所有企图解决这一问题都失败的首要原因是由于未能将多个输入测量值组合到任何令人满意的效率测量中。这些不完善的方法包括了利用一个单一输入(忽略其他所有输入)得到一个平均生产力以及构建得到一个投入与产出之比的加权平均的效率指标。回应劳动生产率,资本生产率等等这些不充分的独立指标,法雷尔提出了可以更充分得处理这一问题的工作剖析法。他的测量方法旨在适用于任何生产组织;换而言之,"从车间到整个经济。"不幸地是,他将数值例子和讨论限于单输入的情况下,虽然他可以确切地阐述多个输出的情况。
法雷尔完成开创性工作 20 年后,为满足能够评估多输入多输出生产经营单位相对效率的令人满意的程序的需求,查尔斯等人基于那些想法,提出了更为强大的方法论,其后被称为数据包络分析(DEA)。DEA 背后所隐含的最初的思想是提供这样一个方法论,在一个可比较的决策单元集中,展现出经营最好的决策单元能够被辨别出来,并可以得到效率前沿面。此外,该方法能够测量非前沿面单元的效率水平,并可以确定如此低效率单元可比较的基准。
相较于例如比率分析的传统财务分析方法或者回归分析,DEA 能提供非常独特且有用的性质。尽管所有方法都有它们的优点和缺点,但是 DEA 最重要的特性是有能力将众多参数同时进行比较并得到一个总体绩效的标量值。在给定的企业组中,DEA 能评价各个企业(通常称为决策单元)的相对有效性。假设这些决策单元通过消耗一组输入能产出各种不同的输出。一般而言,一个决策单元需要一些输入才产出一个或多个输出。然而,在 DEA 中,只需要选择一些输入和输出,依赖于其对于决策单元的效率绩效有多大的影响,为了不淡化了效率分析而使用太多的参数。在任何 DEA 模型计算中,对于输入和输出的选择是最重要的,这是因为不同输入和输出组选择会改变研究的结果。它们在一个产业和另一个产业之间变动,甚至在同一产业内变动,这有赖于已实现的效率分析目标。一开始总是用 2 到 3 个输入(输出)是有利的,随后慢慢地增加数目,记录下每个增加的输入(输出)对于效率值的影响。
DEA 的另一独特特点是使用所有的输入和输出的单元类型不是必须要求一样,只要所有的决策单元使用同样一组输入和输出,且评价效率值单位不变。这一特点给予我们选择输入和输出极大的灵活性,以及提供了比较决策单元相对有效性便利的路径。
2.1.2 数据包络模型
2.1.2.1 CCR 模型
最早的形式是由A.Charnes,W.W.Cooper和E.Rhodes(1978)提出(简称为CCR模型),但其仅能处理具有规模收益不变特征的决策单元的效率评估问题。模型如下:

衡量每个决策单元的效率。如果1*q=且存在一个最优解(,),0,0,****vuv> u>而(,)***qvu是线性规划(1)-(5)的最优解,称 DMU O 为 CCR-有效率。否则,称 DMU O 为 CCR-低效率。当 DMU 低效率时,DEA 模型也给出在低效率和一定基准下与 DMUS 有效率相符的参考集合,我们称之为同侪团体。相较于低效率决策单元,同侪决策单元是最接近有效性的单元,且被观测到在相同或更少的输入条件下,能产出相同或更高水平的输出。这使得低效率决策单元了解到是否存在输入过度浪费或者是否存在改进输出量的可能。
上面提及的规模报酬不变(CRS)DEA 模型所含的意思是决策单元的规模与效率关系不大。为了方便计算,开发了双线性规划模型(1)-(5),将每个决策单元与由样本中所有决策单元线性组合得出的虚拟决策单元进行评价比较,效率值计算如下:

在虚拟决策单元线性组合中jl作为乘数对应于每个决策单元,得出虚拟决策单元输入与输出的权重。每个决策单元与虚拟决策单元相比较,以获知在相等或较少输入条件下,决策单元是否能够比虚拟决策单元产出相等或更多的输出。如果存在这一决策单元,此决策单元是有效的,形成有效前沿的一部分,且1,1,0,00= =="j?jqll.如果决策单元不能满足以上情况,此单元低效率,低效率的程度取决于前沿面上的效率公司。
2.1.2.2 BCC 模型
之后,Banker等人(1984)延伸Charnes等人(1978)的早期工作,提出了BCC模型,使DEA方法可用于评价可变规模收益的生产技术,并在CCR模型的基础上进一步推出纯技术效率和规模效率。也就是把技术效率分解成纯技术效率和规模效率,而且技术效率=纯技术效率×规模效率。
对于任一决策单元 0DMU,其对偶形式的BCC模型可表示为:

在(1)式中,j =1, L,n表示决策单元的个数,( )ximij=1, L,为投入要素,( )yrsrj=1, L,为产出要素,m和s分别为投入和产出变量的个数, 0q为决策单元0DMU的有效值。如若10q=,则决策单元DEA有效;如若10q<,则决策单元DEA非有效。
虽然BCC模型能够区分决策单元的纯技术效率和规模效率,但是与传统DEA效率评价模型一样,其存在缺陷为要求所有投入产出数据都是非负的。然而,在现实当中,某些决策单元在某些年度的某些产出(比如净利润)上会出现负值的情况。
2.1.2.3 加法模型
查尔斯等人(1985b)引进了加法或帕累托-库普曼斯模型,此模型在一定程度上,结合了两个导向。图 5 说明这一想法由 B-A-C 构成的象限在那里任何方向都被允许.
加法模型有一些不同的版本,我们给出了最为基本的,其解决线性最优问题,由下面的式中表示。对于jl变量的凸性约束暗示我们需用可变规模收益模型。由如下模型形成的前沿面与相应的可变规模收益模型形成的前沿面相同,因此当且仅当 VRS 有效,决策单元加法有效解得最优解时所有松弛变量等于 0.显然,规模收益不变模型的生产可能集同样可被使用(图 2.1 有说明)。

由于所得到的各种投入与产出所对应的单位不相称,可能在某些情况下使用如上式中那样简单的松弛变量的加总不太实际。此外,模型中没有提供如 BCC和 CCR 模型的测量低效率的方法。为克服这一问题,查尔斯等人(1985b)提出了
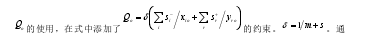
过 iox和 roy将-is和+rs各自分开旨在使这些松弛变量单位保持不变,并乘以d控制整体规模。为了保持与 CCR 和 BCC 模型所测效率的意义的一致性,末吉(1990)提出了 o1-Q的测量法。常和末吉(1991)其文章中认识到的问题是0 ?1-?1oQ规定没有必要,实际情况中可能为负。
由于本文的决策单元(生物制药上市公司)产出中存在负值,所以利用Charnes 等人(1985)提出较为客观的处理方法即所谓 additive BCC 模型,其突出的特点在于所谓"转换不变性(translation invariant)",即对所有投入产出数据加上一个充分大的正数。
2.2 Malmquist生产率指数
Malmquist 指数首先由 Malmquist(1953)提出,用于投入消耗的定量分析。
费雷等人(1994)发展了基于 DEA 的 Malmquist 生产力指数用于测度生产力的变化。该指数可以分成两个部分,一部分测度技术前沿面上的变化,而另一部分测度技术效率的变化。
为了描述这种方法,让tijx,trjy表示决策单元在 t 时间内任何时间点的输入和输出水平。Malmquist 指数计算需要两个单期和两个混合时段的测度。两个单期测度可用使用 CRS DEA 模型。因此,在 t 时段我们通过 CRS-DEA 模型完成效率的计算。
用相同的方式,在上面模型里用 t+1 代替 t,在 t+1 的时段里我们得到了决策单元 oDMU的技术效率值( )11,+ t+ototoqxy.
第一个混合时段测度,其将每个 oDMU定义为( )11,+ t+ototoqxy,最优值的计算是利用如下线性规划问题。
这一模型在时间 t 用t+1ox比较前沿面。用相同的方式,我们能得到另外的混合时间段测度,在时间 t+1 里( )11,+ t+ototoqxy用tox比较前沿面。
这个(输入导向型)Malmquist 生产力指数可以表达为

根据公式(2),全要素生产率TFP的变化即分解为技术效率变化、纯技术效率变化和规模效率变化。技术效率变化大于1意味着技术在考察的年份实现了跨越,即实现了技术进步;纯技术效率大于1意味着管理改善使效率发生了改进;规模效率大于1意味着改变了要素投入,提高了规模效率;TFP变化大于1意味着生产力有所改善。反之,上述指标值小于1,则表明相应效率恶化。





