
一、引言
1995 年,Longstaff 在其经典论着[1]-[2]中,首次运用无套利思想和期权定价理论构造模型,从流动性价值的角度计量了证券“可交易( Marketability) ”的价值,即着名的流动性期权理论。该理论将证券由于不可交易带来的折价视为一个回望期权,认为流动性缺失是导致不可交易或交易受限股票产生折价的主要原因,并基于“投资者完美择时能力”假设得到了流动性折价的最大值,认为“收益波动率是决定折价程度的主要因素”.然而,在将模型结论和实证证据进行比较时,却发现现实的折价程度往往接近甚至高于理论模型得出的最大值,虽然作者认为这仅仅是“非正式的比较”而不是“正式的检验”得出的结果,这一现象仍足以引起我们的关注。而后,研究者们从不同角度对流动性期权理论进行了扩展和应用[3]-[4],但是,并没有最终说明为什么实际观察到的折价会接近甚至高于理论最大值。因此,我们有理由认为,证券的可交易价值中还包含着除流动性价值之外的其他因素。
通过对股票价格行为的观察,发现“可交易”过程带来的其实不仅仅是流动性飞跃,还使股票价格的波动成为可能,同时,真正给投资者带来收益的,更不仅仅是“能卖”,而是“能以不同的价格卖”,正如 Longstaff 的观点,“波动”才是决定流动性折价的主要因素。因此,在股票的可交易过程中波动同样可能具有价值,虽然相对于流动性价值的简单明了而言,波动性价值显得相对复杂,但在适当的背景和假设条件下,还是能够将其分离出来的。本文将对此进行初步尝试,通过考察股票从不可交易到可交易过程简单地说,就是股票的上市过程中形态变化和价值增值的本质,从根源上探讨股票可交易价值的构成和性质,将其分解为流动性价值和波动性价值,分别描述。
二、可交易过程的分解
现实中,股票从不可交易到可交易的过程几乎是在瞬间完成的,且在这一过程中,股票同时获得了可流动性和可波动性。为了研究的方便,我们设想将这一过程分解成两个虚拟的阶段:
---可流动过程。允许股票以固定价格交易,即投资者可以随意买卖股票,买卖行为不受限制,但交易价格不变;---可波动过程。在可流动的基础上允许股票价格随机波动。
这样,我们就可以将股票可交易过程产生的价值分解成两个部分,可流动阶段产生的流动性价值和可波动阶段产生的波动性价值。
令可交易过程中股票的初始价格为 S1,可流动过程结束之后股价为 S2,可波动过程结束之后股价为 S3.有
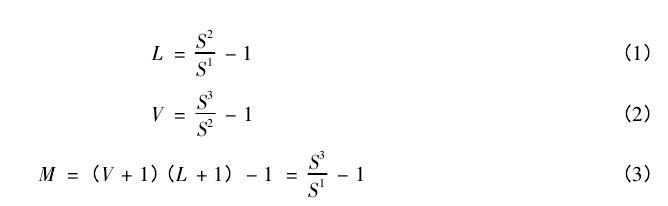
称 L 为股票可交易过程中的流动性价值,V 为股票可交易过程中的波动性价值,M 为股票的可交易价值①,且有 S3= ( V + 1) S2= ( L + 1) ( V + 1) S1= ( M + 1) S1.
事实上,关于股票流动性价值的定义已经不计其数[5]-[6],但这些定义几乎无一例外地将其视为“能以不同的价格买卖”所带来的价值,这中间显然包含着“能买卖”和“以不同的价格”两层含义,因而这些研究无论是从微观结构领域,还是立足于资产定价问题,都必然地在流动性价值中包含了波动性可能的影响,而本文模型中的流动性价值则被定义为“能以相同的价格买卖”所带来的价值,因而彻底排除了波动性的影响。同时,近年来关于流动性与波动性关系的研究认为二者之间是互为因果但又不完全相关的[7]-[8],且已经有研究发现市场层面上,市场波动对股票价格和收益具有显着的影响[9]-[12],而本文模型则是在个股层面上,在“能以相同的价格买卖”的基础上,引入“不同的价格”,独立地探讨波动性可能的价值。换句话说,我们将分别讨论“能买卖”和“以不同的价格买卖”两个问题,即本文模型与以往模型的最大区别在于对股票可交易过程的分解及对流动性价值和波动性价值的分别建模。
三、可流动过程与流动性价值假设
1: 市场无摩擦,具有无限的流动性,投资者是价格接受者。
不可交易的股票经过可流动过程成为可以固定价格交易的股票,其价格也由 S1变为 S2,现实中,这一过程是瞬间完成的。为了对该过程中创造出来的流动性价值进行合理的描述,令 TL= 0 为可流动过程产生的瞬间,存在两项除流动性状况外其他条件均相同的资产 A1和 A2,它们的价格均无波动。资产 A2从 TL= 0 起可流动,价格为 S2,而资产 A1将从 TL= T( T > 0) 起可流动,价格也为S2,而在 TL∈[0,T]时价格为 S1.若理性投资者面临资产 A1和 A2的投资策略选择,则当 S1和 S2之间满足何种关系时,投资者会认为两种策略间无差异? 表 1 显示了上述条件下不同投资策略的现金流分布情况①:

根据无套利原理,策略 1 和策略 2 的收益必须相同,否则将存在无套利空间,因此有
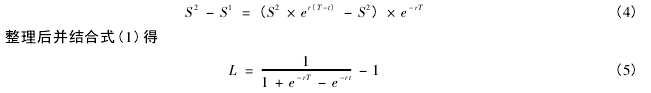
其中 r 为无风险利率,t 为投资者预期提前卖出股票变现的时间。
不难证明 L >0,且 L 是 t 的减函数,即流动性存在正的价值,且流动性价值随投资者预期变现时间的延后而减小。t =0 时,Lmax= erT- 1,表明投资者若在第一时间卖出可流动的股票将可获取最大的流动性价值,其本质即为获取资金的时间价值; t = T 时,Lmin= 0,表明流动性价值会随着不可流动期限的临近而逐渐变小,最终消失。
四、可波动过程与波动性价值
( 一) 假设
假设 2: 研究期间内股票的内在价值不变且投资者站在内在价值的角度看待股票价格的变化。
股票的可波动过程是瞬间完成的,如此短的时间内股票内在价值不可能发生变化; 投资者对波动性价值的预期是站在当前信息的立场上做出的,其对股票价格的未来可能路径的设想亦是基于当前的基本面状况的。
假设3: 投资者的预期波动率 Y 服从均值回复过程( mean-reverting process) ,价格 S 服从几何布朗运动,即
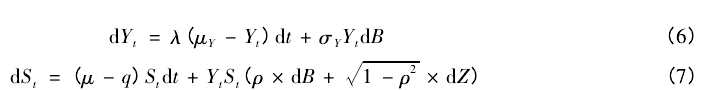
其中,λ、ρ、q 为常数,λ 为波动率的均值回复速度,λ >0 且其取值越大,回复速度越快; ρ 为波动率过程和价格过程的瞬时相关系数,-1≤ρ≤1; q 为连续现金红利率; μY为波动率的长期均值,即投资者的预期平均波动率; σY为预期平均波动率的变动率; B 和 Z 是两个相互独立的维纳过程,且有:
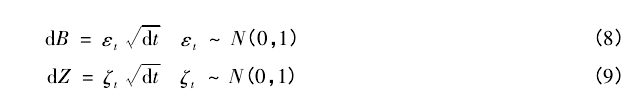
需要说明的是,这里的股票波动及价格路径并非是资产 A3未来可能路径的模拟,而是在股票可波动阶段开始之前,投资者为了评估波动性价值的大小,站在股票内在价值不变的立场上,以 S2为着眼点设想的股票可能的运动规律,其中,初始波动率 Y0= 0,初始价格 S0= S2,其它常数则取决于投资者自身的判断和预期。
( 二) 模型
若投资者持有一单位正处于可交易过程中的股票,令可波动阶段开始时为 TV= 0,此时股票价格为 S2,从下一个瞬间开始,股票价格开始波动。由于内在价值不变,股价可波动前后投资者的预期也就不变,仍为 S2,但由于股价的可波动,投资者多了一种选择: 如果以后时点上股价高于 S2,可以考虑卖出股票获取盈利,是为收益; 而如果波动使股价低于 S2,则可继续持股,并非损失,因为根据假设 2,投资者是站在内在价值的角度看市场的,内在价值不变,投资者对上市公司未来的预期就不变,波动导致的股价的暂时下降并不会给投资者带来损失。而这一选择权的出现使股票完成了可交易过程,其价格也由 S2变为 S3.
再来看这项额外选择权,它是一项权利而非义务,符合标准期权的基本特征。由于持有者可以在任何时点上行权,它更接近于一个美式期权。不同的是,它的执行价格是可交易股票在某时点上的即时价格,是时变的,且它没有明确的到期时间。具体地,令 TV= 0 时,投资者拥有一份可流动但无波动的股票( 资产 A2) ,而从下一瞬间开始,股票价格的可波动使投资者又拥有了一份期权合约( 资产 B) ,赋予投资者在以后的任何时刻以和完全可交易股票( 记为资产 A3) 相同的价格卖出资产 A2的权利。这样,我们就用资产 A2和资产 B 复制了资产 A3,并称资产 B 为波动性期权,令其价格为 C,则资产 A3的价格应为 S3= S2+ C.由于期权价格必定是不小于零的,因此,在本文的假设环境下,可交易过程中波动性价值为正
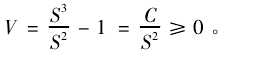 .
.
为了便于求解,我们还要在不影响波动性期权价值的条件下,对其进行适当的变换,将其视为一个行权价格 X 永远等于标的股票初始价格 S0的美式看涨期权( 资产 B‘) .比较 B 和 B',不难发现二者在任何时点上都具有相同的预期收益,也就应该具有相同的价值。因此,下文中将不再区别资产 B 和资产 B'.此外,兼顾假设 2 和现实情况,设期权的有效期 To= 1.至此,我们的任务已经转换为对波动性期权进行估值。
( 三) 模型求解
作为一种路径依赖期权,美式期权的求解往往需要借助数值方法,本文即将采用蒙特卡罗模拟法对波动性期权估值。蒙特卡罗模拟在美式期权估值中的应用始于 Tilley[13],但当时的算法由于计算量过大而几乎无法应用,后经研究者们引入分层法、动态规划思想等,逐步优化算法,减少计算量,才逐步得以在实践中运用[14]-[15].随后,最小二乘蒙特卡罗模拟( Least - Squared MonteCarlo Simulation,LSM) 的提出在这一领域做出了突破性贡献[16],该算法运用最小二乘法确定暂不执行期权的条件预期收益,进而确定最优停时,且仅对期权处于价内的路径进行回归,大大提高了算法的效率,减少了计算的时间。之后,关于 LSM 中回归的时点、路径数与方程数的关系等问题的讨论[17],则使得 LSM 得到进一步的优化,并迅速得到了广泛的应用。因此,本文将采用这一方法求解股票可交易过程中波动性价值的分布特征。
模型求解步骤如下:
第一步,确定相关参数取值,令 r =0. 06、X = S0= S2= 10;第二步,模拟股票的价格路径,令 To= 1,步数为 252,根据式( 6) 模拟股票随机波动路径 997条,对每一条模拟的波动路径,再根据式( 7) 模拟股票价格路径 9998 条;第三步,对每一条模拟价格路径,运用 LSM 算法求最优停时( 具体见文献[16]-[17]) ;第四步,根据最优停时计算波动期权的价格,进而得出波动性价值;第五步,固定其他因素,分别对不同的 q、μY、σY、ρ 和 λ 重复第二至第四步,得到波动性价值的分布特征。
( 四) 分析与讨论
1. 波动性价值的存在---现金红利率的影响
根据传统的金融理论,现金红利率( q) 是股票内在价值最直接的反映。令 λ =2、ρ =0. 50,图 1显示了在不同的 μY和 σY条件下,q 的变化对波动性价值的影响。
可见,随着红利率的提高,股票波动性价值逐渐下降并最终消失,表明投资者可以获得的红利水平越高,股票价格可波动为其带来的价值就越小,当红利水平达到一定程度后,稳定的红利收入已经能够达到投资者的预期水平,波动作为一种额外的选择权,对其已经不再具有吸引力。另一方面,当预期平均波动率( μY) 较小时,波动性价值也较低,其衰减至 0 也就越早,但同样 μY水平下,波动率的变化率( σY) 对波动性价值的影响不大,表现为图中曲线依 μY的不同明显分为两组。
由此可知,波动性价值的存在与否取决于投资者对股票现金红利率的判断,红利率低于一定的水平时,波动性有价值,否则则没有价值。
2. 波动性价值的水平---预期平均波动率及其变化率的影响
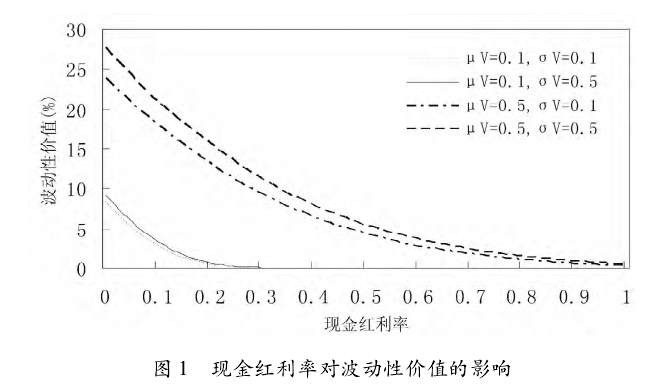
预期平均波动率( μY) 反映了投资者对未来股价波动水平的预期,预期平均波动率的变化率( σY) 则反映了波动受随机因素影响的程度。令 λ =2、ρ =0. 50,图 2 和图 3 分别显示了在无红利( q =0) 及有红利( q =0. 03) 时,不同 σY条件下 μY的变化对波动性价值的影响,及不同 μY条件下波动性价值随 σY的变化。
显然,μY和 σY均是波动性价值水平的影响因素,均与波动性价值呈正相关关系,但比较而言,μY是首要决定因素,其对波动性价值的影响远远大于 σY.主要表现为图 2 中曲线斜率较大但基本交织在一起,而图 3 中曲线斜率小但明显地依 μY的大小分成两组且相互间间隔较大。因此,在内在价值不变的条件下,股价的波动具有价值,预期波动越大,投资者的可能盈利越多; 另一方面,σY对波动性价值的作用程度与 μY的大小有关,表现为图 3 中高 μY组的曲线斜率明显大于低 μY组,说明投资者在预期平均波动率水平较高时,才会更多地关注波动率的变化率,波动性价值对其的反应才更敏感。此外,不同的红利水平对波动性价值曲线的形状和走向没有显着的影响。
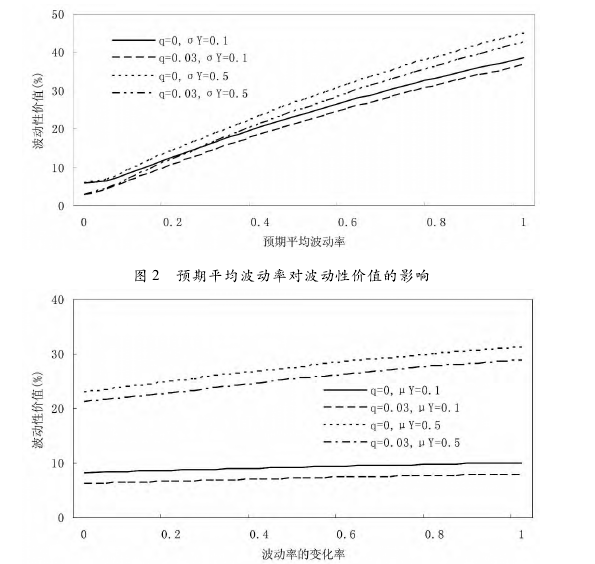
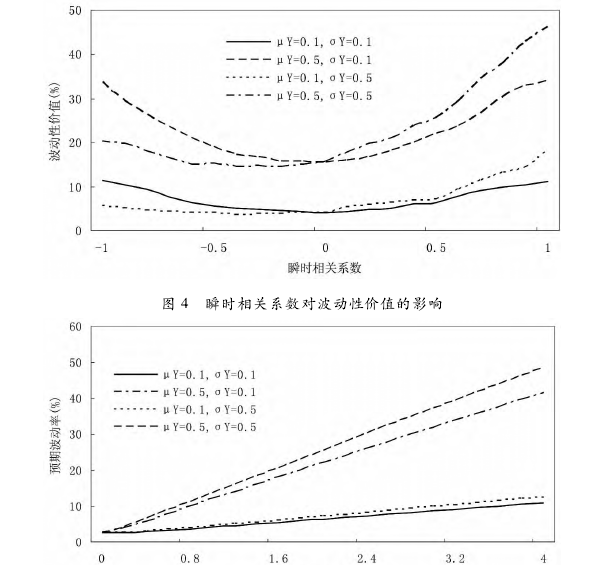
值增加,从实践意义上来讲,λ 大表示波动在偏离投资者的预期之后会很快回复,因而便于投资者把握投资机会,降低风险,实现收益。
最后,图 4 和图 5 中的曲线都根据不同的 μY分成了两组,分别表示了两种不同的 μY水平,再次表明预期平均波动率是波动性价值的主要影响因素。
五、结论与展望
通过对股票可交易过程的分解,我们可以将股票的可交易价值分解为流动性价值和波动性价值,并分别建立流动性价值模型和波动性价值模型。
基于无套利思想的流动性价值模型显示,股票可交易过程中的流动性价值主要表现为资金的时间价值,其大小主要取决于投资者的预期变现时间;在内在价值不变的前提下,股票的波动性可能具有价值,且具有如下特征:
1. 波动性价值的存在与否取决于股票的红利水平,红利率越高,波动性价值越小,直至最后消失。即高额且稳定的红利发放能满足投资者对利润的预期,从而降低其对波动性价值的需求,当红利率达到一定水平后,波动对投资者便不再具有价值。
2. 预期平均波动率决定了波动性价值的水平,是波动性价值的首要影响因素,预期平均波动水平越高,投资者可能获取的收益越大; 预期平均波动率的变化率也是波动性价值的重要影响因素之一,二者也呈正相关关系,但与预期平均波动率相比,其影响程度明显较弱,且其影响程度随预期平均波动率的增大而增强,更多表现为投资者对波动性价值可能存在风险的认识;3. 波动过程和价格过程的相关程度、波动率的均值回复速度对波动性价值的影响主要表现为对其“实现机会”的作用,波动过程和价格过程的相关程度越高,波动过程的均值回复速度越快,则波动性价值实现的机会越大,波动性价值也就越大。
将波动性作为股票价格形成过程中的一个独立因素,实现股票可交易价值中流动性价值与波动性价值的分离,无疑是一种全新的尝试。文中波动性价值存在与否的关键在于股票价格的运动规律是否改变,也就是股票的内在价值是否发生变化,目前我们是通过假设股票内在价值不变实现的,我们或许可以将本文中定义的波动性价值称为“绝对波动性价值”,而寻求一条判断内在价值是否变化的准则,或是研究能够与内在价值的变化形成互动均衡的“相对波动性价值”,将是未来有意义的研究方向。
参考文献:
1. Longstaff,F. A. How Much Can Marketability affect Security Values [J]. Journal of Finance,1995,50( 5) : 1767- 1774.
2. Longstaff,F. A. Placing No arbitrage Bounds on the value of Nonmarketable and Thinly Traded Securities [J].Advances in Futures and Options Research,1995,8: 203 - 228.
3. 梁朝晖,张维。 流动性的期权定价方法 [J]. 北京航空航天大学学报( 社会科学版) ,2005,18( 3) : 8 - 11.
4. Koziol,C. and Sauerbier,P. Valuation of Bond Illiquidity: an Option - theoretical approach [J]. Journal of FixedIncome,2007,16( 4) : 81 - 107.
5. Acharya,A. A. and Pedersen,L. H. Asset Pricing with Liquidity Risk [J]. Journal of Financial Economics,2005,77( 2) : 375 - 410.
6. 陈雨露,汪昌云。 金融学文献通论 - - - 微观金融卷[M]. 北京: 中国人民大学出版社,2006: 178 - 209.
7. Mike,S. and Farmer,J. D. An Empirical Behavioral Model of Liquidity and Volatility [J]. Journal of EconomicDynamics Control,2008,32 ( 1) : 200 - 234.
8. Gillemot,L. ,Farmer,J. D. and Lillo F. There's More to Volatility than Volume [J]. Quantitative Finance,2006,6 ( 5) : 371 - 384.
9. Adrian,T. and Rosenberg,J. Stock Returns and Volatility: Pricing the Short - run and Long - run Components ofMarket Risk [J]. Journal of Finance,2008,63( 6) : 2997 - 3030.
10. Ang,A. ,Robert,H. ,Xing,Y. and Zhang,X. The Cross Section of Volatility and Expected Returns [J].Journal of Finance,2006,61( 1) : 259 - 299.
11. Delisle,R. J. ,Doran,J. S. ,Peterson,D. R. Asymmetric Pricing of Implied Systematic Volatility in the Cross- section of Expected Returns [J]. Journal of Futures Markets,2011,31( 1) : 34 - 54.
12. Li,J. Volatility Components,Leverage Effects,and the Return – Volatility Relations [J]. Journal of Banking &Finance,2011,35( 6) : 1530 - 1540.
13. Tilley,J. A. Valuing American Options in a Path Simulation Mode [J]. Transactions of the Society of Actuaries,1993,45( 1) : 83 - 104.
14. Broadie,M. and Glasserman,P. Pricing American - style Securities using Simulation [J]. Journal of EconomicDynamics and Control,1997,21( 8 - 9) : 1323 - 1352.
15. Grant,D. ,Vora,G. and Weeks,D. Path - dependent Options: Extending the Monte Carlo Simulation Approach[J]. Management Science,1997,43( 1) : 1589 -1602.
16. Longstaff,F. A. and Schwartz,E. S. Valuing American Options by Simulation: a Simple Least Squares Ap-proach [J]. Review of Financial Studies,2001,14( 1) : 113 - 147.





