
拣货作业是仓储管理中一个必不可少的环节,该环节的效率如何、差错率高低直接影响仓储管理运行效率。传统的拣货方法都没有系统地对每种货物在仓库中的位置进行描述,没有建立仓库入口与所拣货物之间的路径几何关系,只是机械地或者主观地根据所拣货物位置以及种类,随机选择一条自己认为比较合适的路线,而没有依据所拣货物的种类及其相互间的位置关系进行拣货最佳路径的计算与设计,使得很多时候仓储人员都会把时间浪费在拣货的流程上。
基于偏离度的拣货方法是近年来兴起的一种比较科学的拣货方法。本文在S形启发方式拣货的基础之上,将基于偏离度的拣货方法结合在一起,根据拣货点与货物存储地点之间的偏差来对拣货的路径进行规划与不断的修正。
1、相关问题的提出
本文研究的是平行拣货通道仓库的拣货路径问题。以某仓储系统的仓库为例(如图1所示),在该仓库中,分拣货物的通道首先可以分为横向通道与纵向通道,其中横向通道数目要少于纵向通道的数目。横向通道主要有前横向通道和后横向通道,纵向通道与货物的摆放呈平行的关系。【图1】

在拣货的过程中,同一条路径到达路径两边货物的距离在本文中忽略不计。在这个仓库中只有一个出口,拣货人员的目的就是从图1左下方的入口进入仓库并在某目标地点拣货然后返回出口。本文就是通过偏离度的方法计算从出口到拣货再回到出口的最短路径。
2、偏离度下的路径优化
本文是在S形启发方式拣货的基础之上来设计拣货路径的。所谓S形启发式的拣货方法,就是拣货人员通过出口进入到仓库以后,从一条纵向的通道进去拣货然后再进入下一个纵向的通道,拣货员的整个路线呈现S形,一直到回到出口完成拣货任务。目前大部分仓储企业的拣货方式都是以此方式为基础的。
2.1 偏离度的概述
在本算法中偏离度的含义是指仓储人员从进入仓库入口处到实际的货物之间的距离,也就是描述了出发地与目标地之间具体的偏差程度,偏差程度由多个偏差度组成。
由于在实际的拣货过程中不一定或者一般都不是单一的某一种货物的拣货,而是多种货物或者多订单一起的拣货。在这种情况下可将偏离度定义为多路径下出发点与目的地点多个偏离度的和。现假设在一次货物的拣货过程中共有I种货物需要拣货,那么实际的偏离度为这I种偏离度之和,假设该仓库系统有K个纵向的通道,那么在每一种货物的拣货过程中其偏离度的计算为几个通道路径之和,可以通过权重系数以及每种货物在第i个通道距离出口点的距离来计算。其中该入口可以是从前向通道进入,也可以是从后向的通道进入。那么综合的偏离度可由所有偏离度综合计算得出。由于是多路径的计算,那么在实际的路径选择中就会出现若干个不同的偏离度,假设路径为m条,那么就会出现相应的多个不同的偏离度。最后可以通过比较多个不同的偏离度来计算最优路径。偏离度示意图如图2所示。【图2】

2.2 偏离度下的路径优化原理
在S形启发方式拣货的基础上,基于偏离度下的路径优化原理实际上是利用了计算机的强大计算能力,假设本次拣货有若干个种类,那么该算法会对每种货物的偏离度进行计算,然后计算出总的偏离度。因为仓储人员拣货方式的种类是可以遍历的,也就是仓储人员对这若干种货物进行拣货,当货物拣货完毕并且回到原始地点的时候,那么其所经历的路径虽然是多种多样的,但是对于计算机来讲这是可以穷尽的。计算机通过计算每一条路径的偏离度得到这若干种物品的一个综合偏离度,然后对比若干种路径的偏离度,最小的偏离度所对应的路径就是仓储人员取货所应该走的路径。拣货通道的示意图如图3所示。【图3-4】


图4为基于偏离度原理的路径优化图,图中黑色的小方块为待拣货的货物,由起始点指向各个货物存储的点的箭头描述了各种货物当前的偏离度,但是由于路径的不唯一造成了偏离度的不唯一,也就是说图中每个物体的偏离度都不是唯一的,而是都具有多个偏离度。如果仓储人员要选择最短的路径即最小偏离度的路径,就要首先通过计算机计算出仓储人员可能走的每一条路径的综合偏离度,然后根据综合的偏离度的大小来确定到底该选择哪一条路径。
2. 3 偏离度下路径优化方法的判断方法
偏离度下路径优化的判断方法就是首先根据此次所拣货物种类的不同,通过计算机对仓储人员所有走过的路径进行计算并进行存储。
确定了每一条路径之后,计算每一条路径针对每一个物品的偏离度,然后再计算该路径下所有待拣货物的综合偏离度,最后每一条路径都会得到一个综合的偏离度。在这些偏离度所对应的路径当中,最小偏离度对应的路径便是该算法下应该优先选择的路径。
(1)最后一个拣货点是k通道
在计算出每条路径所对应的偏离度之后,每个偏离度所对应的路径也就确定了,那么仓储人员所应该走过的路径也就是确定的,图5为经过计算后仓储人员经过最后k通道的路径示意图。【图5】

(2)最后一个拣货点不是k通道
在另外的一个试验中,还是利用随机数的形式让若干个货物随机分布在仓库的各个位置,将其种类以及其相应种类位于哪个通道都记录到计算机当中,并针对若干种货物的分布以及仓库通道的分布计算所有仓储人员可能走过的路径,并将其存储起来。最后计算每条路径上所有物品的综合偏离度,选取最小的偏离度所对应的路径就是要选择的路径。
在该实验中仓库的路径分布以及货物的分布如图6所示,得到的最佳路径在图中已经标出。可以看出在这个试验中该算法的最后一个拣货点不是k通道而是k-1通道。【图6】

3、仿真数据结果的比较分析
假设针对图1中所模拟的仓库,利用S 形启发式方法计算出仓储人员从进入仓库到拣货完成所需要的路径,然后根据拣货点的不同分别计算出多个不同的拣货点所对应的S形启发方式下的路径。再根据偏离度的路径优化方法计算最优路径。经仿真10 次求平均值绘制出表1.以随机拣货点的数量为横坐标,以这两种方法优化计算所得出的对应于特定数量的随机拣货点的路径作为竖坐标,分别取15对点就可以在同一坐标系中绘制出两条具有类似意义的折线,其中一条折线代表S 形启发式方法所得到的随机的拣货点与拣货路径之间的关系。另一条代表偏离度下路径优化方法得到的路径结果与随机拣货点之间的关系,如图7所示。【表1.图7】
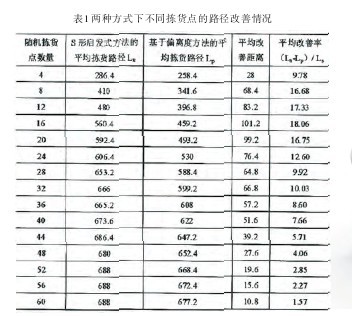

结合表1和图7可以看出,针对同一拣货点的数量,基于S形启发方式下拣货的路径普遍地比基于偏离度的拣货方式所要走的路径长。也就是说基于偏离度的拣货方式要优于基于S形启发方式的拣货方法。














