
一、引言
近年来,对冲基金 (Hedge Fund) 工具在我国日益增多,我国的金融市场环境也日渐成熟,国外对冲基金越来越重视在中国金融市场中的投资机遇,很多国外的对冲基金公司开始向中国进军。但是,由于发达国家有较为完善的金融市场,这给对冲基金的发展提供了良好的发展环境,因此与对冲基金相关的理论研究主要在西方发达国家,包括投资组合理论、资产估值理论、套期保值理论、Black-Scholes 期权定价理论。而我国改革开放刚刚三十年,金融市场的发展更短,因此对冲基金在我国的发展环境与西方发达国家有所不同,这就要求我们不能简单地把对冲基金在西方发达国家的运作模式直接应用过来,我们应当探索适合我国金融市场的对冲基金投资策略。本文结合我国股票市场的实际,运用对冲基金投资的思想,分析将统计套利运用于对冲基金的投资过程,并计算其收益状况。
本文的创新之处在于: 第一,首次尝试在对冲基金对标的股票进行统计套利之前加入 GARP 选股模型,为随后的投资组合挑选出高价值和高成长性的股票; 另外,本文通过对多项指标的分析,基于 GARP 选股模型的思想,挑选出了 11 项能够反映股票成长和价值两方面的指标。第二,本文尝试通过对成长、价值、活跃程度三类指标进行层次聚类分析挑选出相关性较高的股票对,而不是仅仅通过相关系数挑选股票对,这就能够更好地保证挑选出的股票对具有内在和外在的高度相关性。第三,本文尝试使用中心化后的价差进行 GARCH 模型建模,求解其条件方差方程,并通过中心化后的价差与条件方差方程中的残差进行对比来确定交易时机,中心化后的价差剔除了常数项系数的影响,能为我们更好地提供交易时机。
二、文献综述
(一) 国外对冲基金投资及统计套利在对冲基金投资中运用情况综述
对冲基金起源于 20 世纪 50 年代初的美国,在运作初期,主要是通过期权、互换、期货等金融衍生工具和相关联的股票对进行空卖空买,运用风险对冲的操作思想和运作方式,尽可能地规避投资中出现的各种风险。在对冲基金发展 60 多年后,渐渐地成为了一种投资方式,即利用金融衍生工具中的杠杆效应,一方面接受高风险,一方面追逐高收益。
针对对冲基金的分析多以金融理论为基础,并由此衍生出来很多对冲基金的投资策略,包括股票对冲策略、相对价值策略、事件驱动策略、宏观策略,每种投资策略都有多种具体的操作方法。其中统计套利是一种可以脱离市场走势获得稳定收益的相对价值套利策略,在对冲基金中应用普遍,特别是在做空机制的市场中。
统计套利的思想是华尔街交易员 Nunzio Tarta-glia[1]在 20 世纪 80 年代提出的,他所带领的小组发展了基于统计技术的数量化套利策略,开始了统计套利的实践操作,后来 Oleg Bondarenko 和S. Hogan[2]等学者给出了统计套利的严格数学定义。
Andrew Neil Burgess (1999)[3]创新性地提出了一种统计套利动态模型的计算方法,即利用协整和误差修正理论来构建交易比例; G. Vidyamurthy(2004)[4]认为统计套利是基于相对定价,他认为公司相似的股票价格较为接近,定义错误定价的大小为价差,当价差较大时,错误定价的程度较高;Andrew Pole (2007)[5]在着作中从最基本的加权移动平均模型,到复杂的动态因子分析模型建立起了价差和残差①之间的关系,从理论上构建了统计套利模型; Nicolas Hunck (2008)[6]讨论了成对交易中交易组合的选取方法和已选组合的优劣评价方面的问题,以 S&P100 指数样本股为待选股票池,运用Elman 神经网络方法分别预测两两组合的收益。
(二) 国内对冲基金投资及统计套利在对冲基金投资中运用情况综述
国内对冲基金整体发展概况研究综述。程翼[7]于 2001 年编着的 《对冲基金》主要介绍了对冲基金的定义、分类和特征、发展过程和其投资方式,重点分析了对冲基金的收益和风险问题。此外,国内的学术期刊还发表了一些有关对冲基金研究的论文,黄运成[8]等 (2008) 从对冲基金的规模,其分布地域,所构建的投资组合策略以及收益—风险特征等方面对对冲基金进行了分析。在对冲基金实际运用到投资中时,国内学者对对冲基金具体投资策略的研究也起步较晚。张树德 (2009)[9]介绍了传统的对冲基金投资策略的相关原理和特征,讨论了我国目前对冲基金投资策略的发展方向,包括对冲策略精细化、非对冲化策略和数量化投资三种发展趋势; 李伟婷 (2010)[10]研究了国外对冲基金采用的投资策略,主要从多样化投资的策略和理念出发,这给我们了一定的启示; 顾巧明和惠宝成[11](2011) 在分析传统的投资对冲基金组合架构存在不足的基础上,提出了新的资产组合构架模型,从理论上论证了对冲基金更多的是一个风险溢价的提供者,以及将对冲基金与传统资产有机整合到一起更有好处。从上述论文看出,我国对于构建对冲基金投资组合的研究主要基于简单的定量分析上。
具体到统计套利策略在对冲基金的应用中,方昊[12](2005) 从理论上给出了统计套利策略,并对 16 对封闭式基金组合建立投资组合,当价格比值超过或者低于长期均值的偏差超过 1 个标准差,则开始进行交易; 杨勇[13](2009) 给出了统计套利理论模型,当两只协整的股票出现价差时便进行套利,但文章并未给出具体的实证分析; 于玮婷[14](2011) 挑选出相关系数较高的两只股票,并利用静态的价差标准制定其交易规则,寻找套利机会。除了学者,机构投资者对统计套利策略也有所研究,联合证券、中信证券、光大证券和海通证券都进行过统计套利研究,总体偏向于技术型策略。光大证券 (2008) 选择沪深 300 成分股作为标的股票,选取具有协整关系且相关系数最大的股票对,基于市场中性策略和成对交易进行统计套利; 对冲网 (2012) 选取了浦发银行和招商银行两只股票,根据价差建立起的 GARCH 模型,通过价差和条件方差方程中的残差进行比较,选择交易时机。
三、数据、GARP 选股模型及其结果
(一) 数据
2013 年 1 月 25 日,根据证监会公布的通知,上交所能够参与融资融券的标的股票数量从 180 只扩大至 300 只,深交所融资融券标的股票数量由98 只扩大至 200 只。总的来说,我国能够参与融资融券的标的股票范围扩大至 500 只,这就为我们构建对冲基金投资组合提供了利好消息。最近随着“国五条”的出台,房地产行业得到了极大的关注,因此本文选取房地产行业的股票作为对冲基金操作的标的股票。
本文数据来自招商证券智远理财服务平台,房地产行业共有 146 家公司,根据各个公司财务指标数据,采用 GARP (Growth at a Reasonable Price)选股策略挑选出 10 只具有高投资价值的股票。要求挑选出的这 10 家公司满足以下两个条件: 第一,该上市公司的股票属于融资融券的标的股票; 第二,该上市公司已于 2012 年之前上市。
在挑选出来股票对后,要找出套利区间,为了保证数据有效性,本文选取 2011. 01. 04—2012.04. 03 之间的两只股票日收盘价数据作为研究样本。
(二) GARP 策略指标选取及构建模型
1. 指标选取
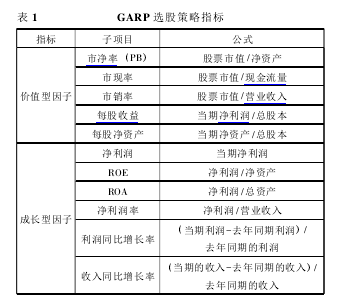
GARP 选股策略是一种结合了价值投资和成长投资策略,试图寻找价值被市场低估,同时又有较强持续稳定增长潜力的股票,具有分散化投资、数量化选股以及收益较稳定的特点。GARP 选股策略将指标分为价值型因子和成长型因子,综合考虑指标的意义各方面因素,本文选择的价值型因子包含5 个子项目,成长型因子包含 6 个子项目,详见表1。右侧指标可以综合反映上市公司的价值和成长状况,保证了通过 GARP 策略选出的股票具有良好的统计套利的特性。
2. GARP 模型构建
根据 GARP 模型的思想,选股时应同时考虑价值型因子和成长型因子。本文对上述指标进行等权重进行加总,选取出得分前十名的房地产公司股票。
3. 数据处理
在选取的数据中存在比率型数据,例如市盈率、净利润增长率等; 也存在数值型数据,例如总资产、净资产等。数据的单位不一致,对后续分析将会产生一定的影响,因此本文将每一个变量的数据进行标准化处理。通常以均值为 0,标准差为 1的正态标准化处理之,公式为: 标准化后变量 =(原变量-均值) /标准差。
(三) GARP 选股结果
在通信达平台上获得房地产行业 146 家企业的11 项指标,包括市净率、市现率、市销率、每股收益、每股净资产、净利润、ROE、ROA、利润同比增长率、收入同比增长率、净利润率。对每一项数据进行标准化,并进行等权重加总得出每个公司总的得分,选出前 10 只股票详见表 2。

四、基于聚类分析构建股票投资组合
实施统计套利策略的关键是通过一定的方法寻找股票价格波动存在高度相关的股票组合,然后对股票价格序列建立交易组合。为了能将选择股票的基本面分析与量化手段联系起来,本文通过能反映一只股票价格波动和内在价值的指标来进行相似度分类。上文从房地产行业中选取了 10 只有投资价值的股票,下面将从这 10 只股票中选出一对股票,股票对中的两只股票应具有高相关性。
(一) 聚类分析
考虑到每只股票的各项指标间可能会存在一定的相关性,所以样本间的聚类采用层次聚类分析法(Hierarchical Cluster Analysis) ,该方法对给定的数据集进行层次的分解,直到某种条件满足为止。
(二) 指标选取
在聚类分析中,为了较为客观全面地衡量两只股票之间是否具有高度的相关性,选取了反映股票内在投资价值的指标,与 GARP 选股策略两方面的指标相同,同时又引入了反映股票活跃情况的两项指标,每笔均量表示成交总量与成交笔数的比值,每笔换手表示每笔均量与流通股本的比值。这三方面指标从价值、成长、活跃程度综合反映股票的状况,保证了层次聚类分析后选取出的股票具有较高的相关性。
(三) 相关性检验
为了验证经过层次聚类分析得到的股票组合是否在价格序列上具有相关性,分别求出每一组股票对与股票价格的相关系数。
(四) 聚类分析结果
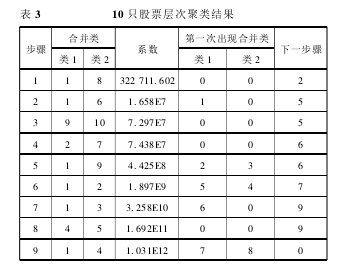
本文对 GARP 策略选取的 10 只股票的成长、价值及活跃度情况指标作层次聚类分析,得表 3。由表 3 可以看出,10 只股票经过 9 次聚类归为一大类。根据上文对选股的要求,可以选出一对股票———保利地产和万科 A。由于万科 A 在 2012 年间有无交易数据的情况,在处理数据时删除了相应日期保利地产的股价,最后共计 286 个交易日数据。
对上述两只股票对进行相关性检验,得到相关系数为 0. 802 3,说明两个股票之间具有较高的相关性,为以后做协整做准备。
五、基于统计套利策略分析投资组合的收益率
统计套利是指用统计方法寻找套利机会的投资策略,其核心是在金融时间序列中运用计量经济学、金融建模的方法来发现套利机会。发现所构建的投资组合中的错误定价关系,并对这种关系建立起动态的模型,进而可以实施统计套利的投资策略。统计套利可以减少市场中的系统性风险,可以产生无风险的超额收益,从而产生低风险、低波动率,但是稳定的收益。随着金融统计软件以及数学建模方法的发展,统计套利模型越来越受到我国机构投资者的关注。本文对上文选取出的股票对通过统计套利策略构建投资组合。
(一) 统计套利具体操作策略
本文使用统计套利中的成对交易策略,这种方法也被称作利差交易。在前文的基础上选取出 1 个股票对,随后确定交易规则及收益率评价标准,运用 GARCH 模型来寻找股票对中的交易机会,并进行统计套利。
(二) 协整检验
本文将协整关系运用于统计套利具体策略中的成对交易策略。在 Eviews 中对每只股票价格进行单位根检验,若两变量的单整的阶不同,则两变量不是协整的,重复聚类分析的过程,重新选取股票对; 若两变量的单整的阶相同,并且都是平稳的,则两变量有可能是协整的。本文通过最小二乘法(OLS) 求出两只股票价格之间的回归方程,在此基础上求出方程的残差序列,当残差序列是平稳的,并且服从正态分布时,这一对股票的价格存在长期就均衡关系,此时统计套利就会变得很容易。
当残差偏离到一定程度时开始建仓,买进被相对低估的股票,卖空被相对高估的股票。
(三) 交易规则及收益率评价
本文将操作区间分为两部分。第一部分,无套利区间,在该区间内视为不存在套利机会; 第二部分,套利区间,在该区间内,对冲基金应积极建立套利组合,卖空高估值的股票,买入低估值的股票。对于套利区间的确定,首先的原则是交易触发的区间,应该大于交易双方的成本,确定该区间的方法有 ARMA 模型、Markov ARMA 模型和非参数模型,基于非参数方法对样本内数据交易区间实证表明,若去除均值之后的价差序是白噪声序列,则最大收益的交易边界是+0. 75σ,本文在前人研究基础上,确定套利区间时考虑交易费用和样本外数据可能出现剧烈波动,最后得出无套利区间 (-σ,σ) ,套利区间 (-∞ ,-σ) ,(σ,∞ ) 。
确定套利区间后,应构建价差序列和残差序列。计算两只股票间的价差为 st= pyt-β×pxt,其中pyt是股票 y 在 t 时刻的股票价格,pxt是股票 x 在 t时刻的股票价格,st是 t 时刻两只股票的价差,β是 x,y 的协整系数。价差序列表明了两只股票股价的差距水平,进而可以根据对价差的分析来构建统计套利的交易策略。根据价差序列均值对该序列进行中心化处理,mst= st-mean(st) ,很多研究在确定交易策略时,直接根据价差序列整体的标准差来确定交易条件,没有考虑价差序列方差会随时间变化而变化,事实上,很多金融时间序列都会随时间发生变化。为了更符合价差序列波动情况,本文用 GARCH 模型来模拟价差序列的变化。本文分析ms,首先判断 ms 是否是平稳序列,并根据 ms 数据特征写出自相关模型,假设滞后性为 n,则 mst= co+c1×mst-1+…+cn×mst-n+εt。
用 GARCH(p,q) 模型估计序列 mst的条件方差方程,可以得出:
σ2t= α0+α1×ε2t-1+…+αp×ε2t-p+γ1×σ2t-1+…+γq×σ2t-q(1)
通过上述模型可以得出每个交易日 mst和 σt的数值,然后可以进行具体的操作,当 mst< - σt时,买入 1 股 y 的股票多头,卖空 β 股 x 的股票空头,具体的资产配置比例,要根据当时的股票价格来确定,建立交易头寸后,mst回落到 (-σ,σ) 区间时,进行反向操作; 当 mst> σt时,卖空1 股 y 的股票空头,买入 β 股 x 的股票多头,其余同上。以相应的每日收盘价作为本日交易的买入价和卖出价。
在不考虑交易成本和融资费用的情况下,每一期的收益可以计算出来:
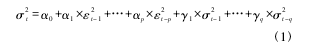
式中,rt是一次完整交易的收益; pxt-1是在此次交易第一天购入相对低估的股票,也即x 的价格; pxt是t时刻进行平仓时的 x 的股票价格; pyt-1是在此次交易第一天卖空相对高估的股票,也即 y 的价格; pyt是 t 时刻进行平仓时的 y 的股票价格。每个股票对样本周期内的收益相加得到每只股票的累计收益率 R。
(四) 实证结果分析
1. 股票对的协整检验
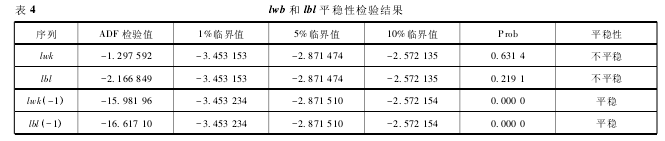
万科 A 和保利地产股价分别记做 wk 和 bl,为了减少舍入误差,对 wk 和 bl 进行自然对数处理,分别记做 lwk 和 lbl。对 lwk 和 lbl 两个序列进行平稳性检验,详见表 4。

结果显示,lwk 和 lbl 本身都不是平稳序列,但是它们的一阶差分是平稳的,表明两者之间可能存在协整关系。用最小二乘法求出两个价格对数序列的回归方程为: lwkt= 0. 277 7+0. 806 4×lblt+εt,t=(3. 411 9)(23. 479 8) ,R2= 0. 66。对残差 εt进行平稳性检验,发现 εt是平稳的,也即求对数后的两列数据就有协整关系。
2. 根据交易时机进行投资的收益率情况
由于 lwk 和 lbl 具有协整关系,可得 lwk 和 lbl两个序列的价差为: st= lwkt-0. 806 4×lblt,再根据价差均值 mst =st-mean(st) 。
对该序列进行中心化处理得到 mst。用 GARCH模型计算价差序列的条件异方差来代替价差的简单标准差,由于价差 st包含了回归方程 lwkt= 0. 277 7+0. 806 4×lblt+εt中的系数信息,因此本文采用中心化后的价差 mst。分析 mst序列的自相关函数和偏自相关函数,初步判断 mst是一个自回归过程: mst=0. 000 5 + 0. 995 6 × mst-1+ μt ,其中 t = (0. 770 4)(112. 732 3) ,R2= 0. 978 2。对上式进行条件异方差的 ARCH-LM 检验,得到了滞后阶数为 5 时的结果,其中 F 检验结果为 3. 048 4,Prob. F(5,274)为 0. 01,可以看出 mst具有 ARCH 效应,用 GARCH(1,1) 建模得到表 5 结果。
写出条件方差方程的表达式为: σ2t= 0. 588 1×μ2t-1+0. 435 6×σ2t-1(3)式中,μ2t-1表示用均值方程的扰动项平方的滞后,用来度量从前期得到的波动性的信息; σ2t-1是上一期的预测方差。
本文运用 2011. 01. 14—2011. 12. 30 共 239 个交易日股票价格求价差,并求出价差的无条件方差为 0. 145 6,作为异方差方程的初始值,因此可以得到随着时间变化的残差 σt的值。
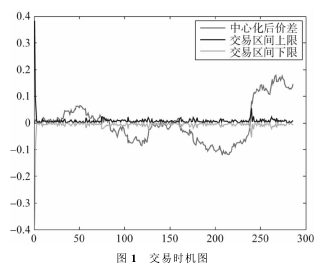
将条件方差方程的预测方差和中心化后的价差用图 1 表示。
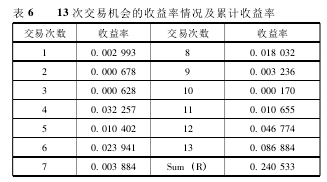
结合上表和 Excel 中计算出的数据显示,在2012. 01. 04—2013. 04. 03 时间段中共有 19 次套利机会,其中套利机会出现在当天的共有 6 次,考虑到交易难以捕捉,予以删去,剩下 13 次。当交易条件出现时,建立头寸进行交易,并且进行逐日盯市制度,使该头寸处于开放状态,也即不进行任何操作,直到价差恢复至均衡水平,随后进行平仓,相应的一个交易期结束,对每个交易期间找到其对应的股票数据。在不考虑交易成本费用的情况下,按照公式 (2) 计算其收益情况。详见表 6。
由表 6 可以看出由统计套利构建的股票对累计收益率达到 24%,收益率较高。
六、结论分析
首先,本文分析了对冲基金的投资策略,以及统计套利的方法,并将其运用到对冲基金投资策略中的股票多头/空头中,利用目前我国股市可以开展融资融券交易来进行股票多头和空头; 其次,本文选房地产行业股票作为对冲基金投资的标的股票,通过对指标的筛选建立起 GARP 选股模型,在房地产行业 146 只股票选取出具有投资价值的10 只股票,用聚类分析选取出成长价值、波动情况高度相关的一个股票对; 再次,构建股票投资组合,制定股票对投资的比例关系; 最后,制定套利区间标准,在 GARCH 模型得到的条件方差 (动态标准差) 构建出的套利区间下,求出收益率情况。
对冲基金的主要思想是通过对冲的方式避免或降低风险,通过本文可以看出统计套利策略可以很好地获得收益并规避风险。统计套利是一种无风险套利条件,损失远远小于预期收益。本文运用统计套利策略投资于相关联的公司股票,它们在内在方面具有一定的相似性,另外它们又受到共同外因的影响,因此对相对价格的发展趋势分析在某种程度上可以忽略不确定因素,通过对相对价格的统计套利可以获得较高收益。





