
反射 CEV 过程是经典 CEV 过程的扩展,通过在该过程中加入 Harrison[1]调节过程,能使 CEV 过程的状态空间被限制在某些特定的开、闭区间内。在反射CEV 过程中,取合适的漂移率 μ 和不变弹性方差尺度参数 β,其可包括几个着名的扩散过程,如反射布朗运动、反射几何布朗运动、反射 Ornstein - Uhlenbeck 过程以及反射平方根过程。另外,需指出: 在利用 CEV 过程描述的金融市场中,当不变弹性方差尺度参数 β≤0时,存在唯一的风险中性鞅测度,而当 β >0 时,则不存在等价鞅测度[2].
在简约形式下,可违约债券风险中性定价公式是由利率、违约强度和违约回复率联合确定的。在大部分已有的研究中,如: Cathcart,L. 和 EI - Jahel L.[3],Duffie D. 和 Singleton K.违约回复率 X 只是被假设为区间[0,1]间的常数。例如 X =0 表示零回复,即当公司违约发生时,债券持有者将不会收到任何回报。而 X =1 则意味着违约并未发生。近期,巴塞尔委员会( Basel Committee) 已经报告: 违约回复风险是违约风险中的一个重要组成部分。显然常数回复率不能完全刻画回复风险。Chiang 和 Tsai[5]用 Cox - Ingersoll -Ross( CIR) 过程描述回复率期限结构,但却并未考虑回复率 <1 的限制,这相应地给模型校准带来了困难。
文中提出了一个反射回复期限结构,即用状态空间为[c,1]( 0 < c < 1) 的反射 CEV 过程建模违约回复率动态。
1 可违约债券定价
设( Ω,F,( Ft∶ t≥0) ,P) 是一个风险中性的过滤概率空间,其中过滤 F = { Ft∶ t≥0} 满足通常条件,且这一风险中性概率空间支撑着一个 F - 适应的标准布朗运动 W = { wt∶ t≥0} .假设违约回复率 X = { Xt∶ ≥0}是如下反射 CEV 方程的唯一强解:
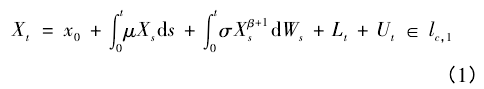
其中,0 < c <1 表示违约回复率的反射边界,状态空间lc,1=[c,1],初始水平 X0= x0∈lc,1,u≠0 为漂移率,σ > 0 为波动尺度参数,β≤0 为不变弹性方差尺度参数,且非负随机过程 L = { lt∶ t≥0} 与 U = { Ut∶ ≥0} 称为在反射边界 c 和 1 的调节过程。L 和 U 由下列性质唯一确定: ( 1) t→Lt和 t→Ut都是连续、单调不减过程且 L0= U0= 0,t∈R+.( 2) L 和 U 分别只有在 X = c 和X = 1 时才会增加,即对所有的 t≥0,下面等式以概率 1成立∫t0I( Xs= c)dLs= Lt,∫t0I( Xs= 1)dUs= Ut.当违约回复率被建模为 RSDE 式( 1) 时,可违约债券的风险中性价格[7]为P( t; T) = E[e-∫Tt( γ+λXs) dsFt],0 ≤ t ≤ T在此 E 是对应于风险中性概率测度 P 的数学期望算子。由于 RSDE( 1) 的强解是马氏的[8],则存在一个R+× lc,1上的可测函数 V( t,x) 使 V( t,Xt) = P( t; T) ,其中 0≤t≤T.接下来,要试图寻求价格函数 V( t,x) 的闭形式表示。
为此,首先定义如下的二阶微分算子
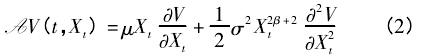
成立∫t0I( Xs= c)dLs= Lt,∫t0I( Xs= 1)dUs= Ut.当违约回复率被建模为 RSDE 式( 1) 时,可违约债券的风险中性价格[7]为P( t; T) = E[e-∫Tt( γ+λXs) dsFt],0 ≤ t ≤ T在此 E 是对应于风险中性概率测度 P 的数学期望算子。由于 RSDE( 1) 的强解是马氏的[8],则存在一个R+× lc,1上的可测函数 V( t,x) 使 V( t,Xt) = P( t; T) ,其中 0≤t≤T.接下来,要试图寻求价格函数 V( t,x) 的闭形式表示。为此,首先定义如下的二阶微分算子
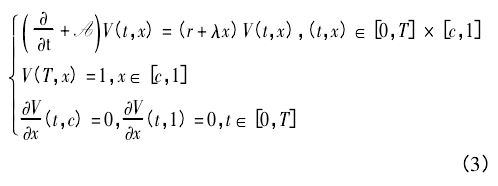
其中算子 A 被定义为式( 2) .对上述偏微分方程组进行时间倒置,令 τ = T - t,则有
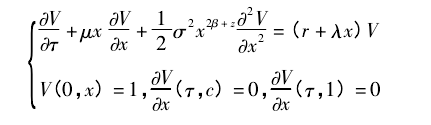
这是一个已知初值条件方程组。利用变量分离法,令。
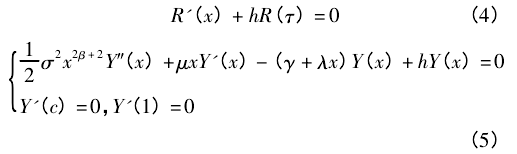
对于式( 4) ,R( τ) =e- hτ; 对于式( 5) ,这是一个 Sturm -Liouville( S - L) 问题。由于 V( t,x) 为光滑函数、其终值条件及 S - L 问题特征值和特征函数的性质[10],因此可得 V( t,x) 具有级数表示形式。那么主要问题是求解上面所述的 S - L 问题。应先考虑 β <0 的情形:
定理 1 假设违约回复率 X 满足 RCEV 方程,那么当 β <0,u≠0 时,价格函数 V( t,x) 具有如下的解析级数表示:
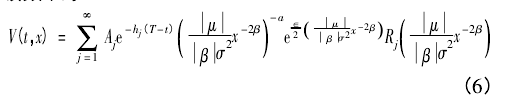
其中权重系数数列{ Aj,j∈N} 满足:


这显然是一个 S - L 方程,且相应的边界条件为式( 7) .
故由 S -L 理论 V( t,x) 可表示为式( 6) .
其次当 β =0 时,违约回复 X 率服从反射几何布朗运动( RGBM)dXt= μXtdt + σXtdWt+ dLt- dUt此时,便有定理 2 假设违约回复率 X 满足 RGBM 方程,则V( t,x) 可表示为下式:
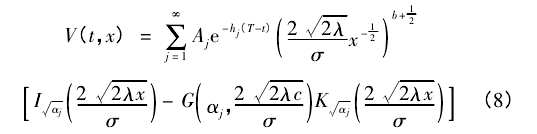




2 仿真实验
违约回复率 X 服从 RBM,可违约债券风险中性价格函数 V( t,x) 具有级数表示式。这里取下反射边界c =0. 4,利率 r = 0. 3,波动率 σ = 0. 1,交割期 T = 1,价格函数随违约回复率和违约强度的变化趋势,如下图所示。
图 1 所示为零时刻价格函数 V( t,x) 随违约回复率 X 的变化趋势。可观察到: 对于固定的违约强度λ = 0. 3,价格函数 V( t,x) 随违约回复率 X 的增大而上升,这与金融市场中的变化规律相符。当债券持有者所面临的风险一定时,若违约发生其所得到的回报越大则债券的价格越大,但不会超过无息债券的价格。
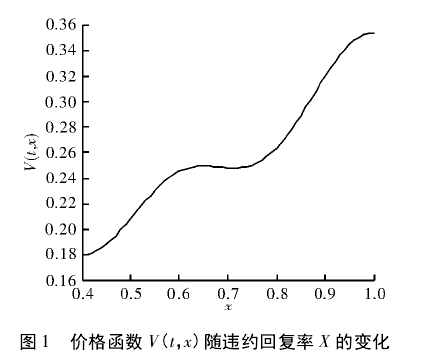
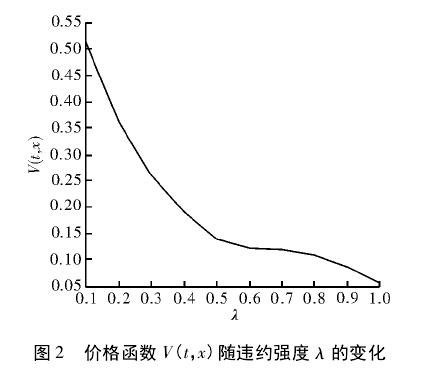
图 2 是零时刻价格函数 V( t,x) 随违约强度 λ 的变化趋势。可观察到; 对于固定的违约回复率 X =0. 4,价格函数 V( t,x) 随违约强度 λ 的增大而下降,这与金融市场中的变化规律相符。在给定违约回复率的情况下,违约强度增大则公司破产的可能性越大,即债券持有者所面临的风险也将越大,故而债券的价格便会降低。
3 结束语
针对可违约债券定价中的违约回复率建模问题,提出了一个反射回复期限结构,用状态空间为[c,1]( 0 < c <1) 的反射 CEV 过程建模违约回复率动态。在此框架下,利用恰当的变换和 S - L 理论推导出可违约债券风险中性价格函数的解析表达式。仿真实验证了,所提出方法的正确性,其能更好地刻画出实际的违约问题。而用马氏调节反射 CEV 过程来建模违约回复率进而推导可违约债券风险中性价格函数的解析表达式将成为进一步的研究重点。





