
γ 射线的角分布测量和极化测量对 γ 谱学的研究有着重要的意义,它们是研究原子核结构和特性的重要方法. 通过该测量能够验证原子核的跃迁方式,给出原子核的自旋和跃迁性质. 原子核由激发态跃迁到基态,有时要连续的通过几次γ 跃迁,这时放出的辐射称为级联 γ 辐射. 原子核放出一条 γ 射线后,接连地放出其级联γ 的概率 W 与两级联 γ 的夹角θ有关,即 W 是 θ 的函数———角关联函数[1].
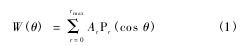
W(θ) 表示γ1和γ2之间夹角为θ时的相对概率,Pr(cosθ)为勒让德多项式,r 为偶数,通常只取到 4即可. 图 1 为笔者根据理论值[1]画出的不同跃迁方式的级联γ辐射的角关联函数,横坐标为角度值(弧度制),纵坐标为 W,图中数字表示不同跃迁方式,其中 42220 代表60Ni 的级联跃迁方式. γ1和 γ2级联跃迁通常以 Ia(L1)Ib(L2)Ic来表示[1],其中 L1和L2表示 γ1和 γ2的角动量;Ia,Ib和 Ic分别表示原子核始态、中间态和末态的自旋. 因此 42220 表示60Ni的 1 173. 3 keV 和 1 332. 5 keV 两条 γ 射线的角动量都是 2,初始态、中间态和末态的自旋分别为 4、2和 0.
1、 实验方法
为简化实验,本文只测量 90°和 180°的符合计数率并通过下式得到各向异性度 A 的值:

根据理论计算,对60Ni 来说 A = 0. 166 7. 通过将实验测得的各向异性度与理论值比较,就可以定出60Ni有关能级的自旋以及其γ辐射的级次,即其跃迁方式.
针对本实验要求,我们自行设计了实验平台,如图 2 所示. 整个平台主要分为两部分:中间的支撑架和两条可近 360°旋转的支撑臂. 支撑架的底盘上绘制角度刻度,支撑臂上各有一滑块,可移动,用于承载和固定探测器.
实验中选用的闪烁探测器为法国圣戈班公司生产的 3 英寸 × 3 英寸的溴化镧探测器和 5 英寸 × 5英寸碘化钠探测器. 这两个探测器体积大且探测效率高是该实验顺利进行的关键. 但同时,由于几何尺寸较大探测器不能简单地理想化为点,因此需要就实际实验情况对理论值进行修正.
我们选用活度为 100μCi 的60Co 源进行实验. 它的衰变纲图如图 3 所示.
60Co 发生 β 衰变后变为处于高能级(2505. 8 keV)的60Ni,之后60Ni 便会级联地放出 1 173. 3 keV 和 1 332. 5 keV 两条 γ 射线. 对于60Ni,我们采用符合的方法来保证公式(1) 中测得的信号来自于同一次级联 γ 辐射.



2、 理论修正
因为本文选用的探测器体积较大,而且为保证计数率在可接受范围内,探测器不能离放射源太远,所以θ并非严格的 90°和 180°,而且不同角度上由于穿过探测器的路径不同,探测效率也会变化,所以我们需要对式(1)中的 Ar利用加权积分的方法进行修正. 关于详细的修正方法,前人已经给出[2].
进行实验时,碘化钠探测器距放射源 30. 5cm,溴化镧探测器距离放射源为 20. 5 cm,探测器的尺寸已知. 这样按照参考文献[2]中的方法就可以对式(1)角关联函数进行修正,并最终得到修正过的各向异性度 A =0. 164 7.
3、 实验方法及电子学线路
实验电子学线路如图 4 所示. 笔者利用定时甄别器(ORTEC 584)阈值设定功能设计了类似于单道功能的电路. 同一探测器输出的脉冲信号分为两路,输入到两个设定不同阈值的定时甄别器中,这两个阈值之间就是我们感兴趣的能量段. 将两路信号输入到反符合单元中,下阈信号输入到反符合端. 这样当探测器探测到的射线能量介于此上下阈之间时,反符合单元就会输出脉冲信号. 用此脉冲信号做门信号,将探测器输出信号输入到多道分析器(OR-TEC Aspec927)中,就能看到上下阈之间的能谱. 这样做的目的是为了将两条γ射线的全能峰信号甄别出来,这样能够避免两探测器之间康普顿信号的cross - talk 效应,提高实验精度. 实验中我们取溴化镧探测器的 1 173. 3 keV 全能峰信号和碘化钠探测器的 1 332. 5 keV 全能峰信号进行信号处理.

实验中利用符合计数与两全能峰计数之比来代表 W,即碘化钠探测器的计数为 N1,溴化镧探测器的计数为 N2,符合计数为 Nc,假设这两个探测器的效率分别为 ε1(θ)和ε2(θ),入射的γ光子数为 N0,则有

这样利用两个探测器的计数 N1和 N2以及符合计数 Nc就可以得到 A. 这样做的原因是由于在实际实验中很难将放射源正好放在支撑架的中心,所以在转换角度后各路计数和符合计数都会变化,而这种变化跟角关联没有关系. 因此本文的方法可以消去这种变化的影响,而且由于单路计数远大于符合计数,因此不会对精度造成很大的影响.
将所有的装置按照图 4 进行搭建,阈值调节合适后就可以输入到计数器中,三路同时计数,一段时间后改变角度,重新计数.
4、 实验结果分析
最终得到的实验结果如表 1 所示,几组数据实验条件完全一致,仅仅改变卡峰时的阈值. 可以想见,阈值在较大范围内变化仅仅会影响单路的计数,对各向异性度不会有较大的影响. 以第一列数据为例,根据式(1)中提到的 W 计算方法和式(2),最终得到:A =0. 166 5. 经过计算偶然符合[3]基本上可以忽略,统计误差是最主要的误差. 根据统计误差的定
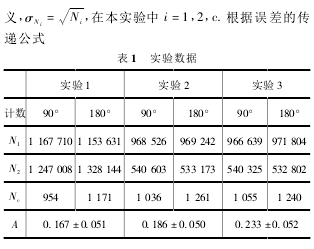

最终得 σA= 0. 051,即 A = 0. 167 ± 0. 051,与修正过的理论值完全符合. 与此实验值对应的理论跃迁方式是 42220,这也和实际的60Ni 两个级联 γ 射线能级自旋对应. 同理可得,实验 2 中 A = 0. 186 ±0. 050. 对3 次实验应用加权平均

其中 Ai和"i分别为各次实验得到的各向异性度和误差,将表 1 中的数据代入,可以得到 3 次实验各向异性度的平均值和最终的误差,最终的结果为 A =0. 195 ± 0. 029. 得到的平均值在误差范围内和修正过的理论值比较接近,说明实验方案可行,但实验精度尚需要进一步的提高.
5、 结论
通过实验测量值及理论修正值,两者符合得较好. 说明我们自行设计的实验平台及方法是简单可行的,在实验教学上值得推广. 该实验有助于学生对原子核的γ衰变和级联γ辐射物理现象的理解,并且通过此实验使得学生的基本核物理实验技能得到提高.
参考文献:
[1] 卢希庭. 原子核物理[M]. 北京:原子能出版社,2000:141-144.





