摘 要: 质子治疗过程容易受射程偏差、摆位偏差、患者解剖结构改变等不确定因素的影响,质子调强放疗的鲁棒性优化是将这些不确定因素考虑进计划的制定过程中,增加治疗计划鲁棒性的一种方法,在临床中有广泛的应用。鲁棒性优化的方法主要有4种:(1)概率法;(2)最差剂量法;(3)添加约束项;(4)多CT优化。本文综述了这4种方法的原理、优缺点和临床应用情况。同时,还介绍了治疗计划鲁棒性的评估方法。虽然目前剂量体积直方图束是最常用的评估治疗计划鲁棒性的方法,但是,剂量体积直方图束不能反映质子调强放疗计划对解剖结构改变的鲁棒性,因此,还急需建立一个简单易用并能被广泛接受的鲁棒性评估方法,方便质子调强放疗计划的对比和评估。
关键词: 质子调强放射治疗; 鲁棒性优化; 鲁棒性评估; 综述;
Abstract: The intensity modulated proton therapy(IMPT) process is susceptible to factors such as range uncertainties, setup uncertainties and anatomical changes. The robust optimization of IMPT is a method to increase the robustness of treatment plan by taking these uncertainties into consideration in the process of optimization, which is widely used in clinical practice.There are four methods for robust optimization:(1) probability method;(2) worst dose method;(3) adding constraints;(4)multiple CT optimization. This paper reviews the principles, advantages and disadvantages of these four methods and their clinical application, and it also introduces the evaluation methods for robustness. Although the dose volume histogram(DVH) bands is the most commonly used method to evaluate the plan robustness, DVH bands cannot reflect the robustness of IMPT plan with anatomical changes. Therefore, it is urgent to establish a simple and widely accepted robustness evaluation method to facilitate the comparison and evaluation of IMPT plans.
Keyword: intensity modulated proton therapy; robust optimization; robustness evaluation; review;
前言
质子调强放疗(Intensity Modulated Proton Therapy,IMPT)相比于传统的光子调强放疗(Intensity Modulated Radiation Therapy,IMRT)有剂量上的优势[1,2,3,4],但是,IMPT的剂量线梯度大,容易受不确定因素的影响[5]。质子治疗过程中的不确定因素大致分为3个方面:(1)质子束本身或由CT值转换为阻止本领而产生的射程偏差;(2)摆位偏差;(3)患者解剖结构的改变,如肿瘤退缩、体重降低等[6,7]。这些不确定因素的存在使得实际照射剂量与治疗计划中的剂量可能有很大不同,使治疗计划的可信度降低,甚至在临床中产生不可预测的结果。比较理想的解决方式之一就是将这些不确定因素考虑进IMPT计划的制定过程中,增加IMPT计划的鲁棒性。
目前,IMPT与IMRT类似,也用计划靶区(Planning Target Volume,PTV)考虑治疗过程中的不确定因素。光子剂量分布的空间特性受不确定因素的影响较小,质子束的剂量分布与射束穿过路径上的密度高度相关,射束路径上的非均匀介质会恶化射程偏差对剂量分布的影响,降低治疗计划的鲁棒性,多篇文章都指出,常规基于PTV的IMPT计划不能精确地考虑射程偏差和摆位偏差带来的剂量变化,从而不能很好地保证治疗计划的鲁棒性[8,9,10,11]。
临床中也会采用单野均匀剂量(Single Field Uniform Dose,SFUD)优化以增加治疗计划的鲁棒性[12]。SFUD优化是单个射野的笔束强度单独优化,不考虑其他射野的影响,优化的目标是满足每个射野都在靶区产生均匀的剂量分布,靶区外的剂量尽可能低。与SFUD优化对应的是多野调强优化(Multi-Field Optimization,MFO),MFO是所有射野的笔束强度同时优化,最终满足靶区和危及器官的剂量要求。由于MFO中每个射野、每个笔束的强度以及对应的靶区剂量通常是高度不均匀的,在射野剂量叠加时就需要保证射束的位置足够精确,否则射束的剂量就无法精准匹配,因此,不确定因素对MFO的影响比SFUD优化大[13,14],但是,SFUD优化给IMPT计划优化增加了额外的限制条件,这会使计划质量受到不必要的妥协,相比之下,MFO则有更大的优化空间,对于复杂解剖结构和复杂剂量分布的情形可以产生更优的剂量分布,有剂量上的优势。MFO是IMPT技术的主流,也是鲁棒性优化研究的重点,为了叙述简单,本文后续提到的IMPT优化均是指MFO。
鲁棒性优化是在逆向优化过程中考虑射程偏差、摆位偏差和解剖结构改变这些不确定因素的一种方法,与常规优化方式相比,采用鲁棒性优化制定的治疗计划对不确定因素的敏感度明显降低。本文的目的是论述鲁棒性优化的原理、评估方法和在IMPT中的应用问题,供临床应用和研究参考。
1、 鲁棒性优化的原理
在逆向优化中考虑射程偏差、摆位偏差和解剖结构改变这些不确定因素的方法主要有4种:(1)概率法;(2)最差剂量法;(3)添加约束项;(4)多CT优化。为了便于介绍这4种方法的原理及特点,这里首先定义一些变量和函数:笔形束的权重为ω,质子束射程为ρ,患者摆位偏差为?s,剂量为D,目标函数为E,发生偏差的概率为P。
1.1、 概率法
概率法假定射程偏差和摆位偏差是统计上两个相互独立的随机变量,这样照射剂量和目标函数也都是随机变量,通过优化目标函数的期望值来考虑存在射程偏差和摆位偏差的情形[15,16]。概率法还假定不同方向射野的笔束偏移是独立的,同一射野的笔束偏移是一致的,不考虑同一射野中有些笔束射程增加有些笔束射程减小的情形。概率法的优化目标函数<E (ω)>可以用公式(1)表示,利用优化算法使<E (ω)>最小。
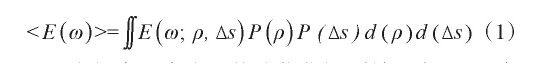
在概率法中为了能让优化问题易于实现,只有部分体元和情形用于估算目标函数值,文献[16]在优化的每一步产生10种发生射程偏差和摆位偏差的剂量分布,每种情形随机地取不同的体元集合,估算目标函数值。
1.2、 最差剂量法
射程偏差和摆位偏差是随机的,如果考虑所有偏差出现的情形需要大量的计算资源,为了减小此问题的复杂性,最差剂量法与概率法一样,也假定不同方向射野的笔束偏移是独立的,同一射野的笔束偏移是一致的,除此之外,最差剂量法还将摆位偏差分成前后、左右、头脚这6个方向,并假定偏差的大小是固定的(通常为3~5 mm),这样对于摆位偏差,每个体元i就产生了6种剂量分布Di1~Di6。再考虑2种有射程偏差(通常为±3.5%)的情形Di7和Di8,以及无偏差的情形Di0,最差剂量法对这9种情形(Di0~Di8)中的最差剂量分布Diworst进行优化。本质上最差剂量优化[8,17,18,19,20]、最小化最大值优化[21]都是最差剂量法优化。
最差剂量法优化把每个体元独立对待,最差剂量的定义如下:

最差剂量法优化假定当一个体元出现最差剂量的时候另一个体元也是最差剂量,很明显这种情形在物理上是不真实的。但最差剂量可认为是治疗计划质量的最差估计。有文献研究表明,处方剂量覆盖靶区的鲁棒性随优化过程中保守性的增加而增加,这也就意味着使用最差估计的方法是值得的[22]。
与最差剂量优化不同,最小化最大值优化考虑了体元之间剂量的联系,它把每一种情形下的剂量分布看成一个整体,只优化物理上存在的情形,计算每种情形的目标函数,优化使最大的目标函数最小[21],其数学模型可用式(3)表示:
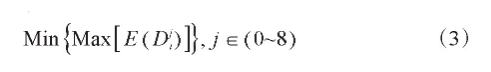
与概率法相比,最差剂量法的优点是不需要射程偏差和摆位偏差的详细模型,只需要少量的计算,因此计算速度更快,这些原因使得最差剂量法在临床中应用最为广泛,多数的商用计划系统中已集成了基于该方法的鲁棒性优化算法。
1.3、 添加约束项方法
添加约束项方法通过两步增加IMPT计划的鲁棒性,首先扩大靶区并用函数压缩照射野在靶区中产生的剂量梯度,保证有不确定因素存在时的剂量能覆盖靶区[23],然后增加函数f2,f2中定义了每个笔束的危险因子Q和产生射程偏差和摆位偏差的可能性P,避免在不确定情形下危及器官受到高剂量照射[24]。若常规优化的目标函数为E0,那么添加约束项方法的数学模型可写成式(4):
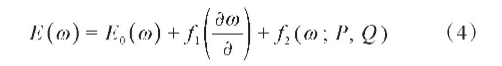
这种方法的原理不直观,并且Q和P的值非常依赖于物理师的经验,所以在临床中应用的报道不多见。
1.4 、多CT优化
上述3种方法都没有考虑患者解剖结构的改变,多CT优化是近两年提出的方法,每套CT都获取了特定情况下患者的解剖结构,在优化过程中采用患者的多套CT就可以考虑患者的解剖改变,通过同时优化患者的多套CT目标函数,可以改善放射治疗计划对解剖变化的鲁棒性[25,26,27,28]。若第n套CT的目标函数为En,则多CT优化的数学模型可用式(5)表示:
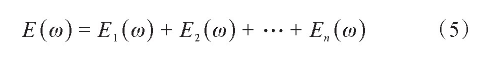
虽然现有研究结果显示,多CT优化可以在一定程度上减少自适应计划的次数[26,27],但是目前从计算速度方面考虑,在计算时En还没有考虑射程偏差和摆位偏差,以后,随着计算机计算能力的增强,多CT优化中也会逐渐考虑这些不确定因素。
2 、治疗计划鲁棒性的评估方法
考虑IMPT计划的鲁棒性是计划评估过程的一个基本要求。由于不确定因素的存在,无偏差的剂量分布不能很好地代表实际的剂量分布。IMRT通常用PTV来定义处方剂量和报道剂量-体积参数,然而,鲁棒性优化考虑了治疗过程中的不确定因素存在时的剂量扰动,也就是隐性地对靶区和危及器官加了外扩边界,如果优化目标也使用PTV,相当于不确定因素被考虑了两次,所以鲁棒性优化过程中靶区目标函数值的计算都是基于CTV而不是PTV,这点与常规基于PTV的优化方式不同,计划评估的方式也会不同。
现有的治疗计划系统只能在静态结构上显示剂量分布,鲁棒性优化包含了射程偏差、摆位偏差和解剖结构改变这些不确定因素,理论上提高了治疗计划的鲁棒性,但是很难从静态结构上定量地确定治疗计划鲁棒到什么程度,尤其在复杂的临床环境中。剂量体积直方图(Dose Volume Histogram,DVH)是计划评估常用的工具。设定不确定因素的具体值,将计划重新计算后就可以得到与设定的不确定因素对应的剂量分布,每个器官的单条DVH曲线很难精确地描述器官的实际受量,评估不那么直观。Lomax[7]提出使用极端情形下的剂量计算分布,最大/最小剂量偏差直方图评估IMPT治疗计划的鲁棒性。Albertini等[12]建议用偏差体积直方图(Error-bar Volume Histograms,EVHs)评估,EVHs中的值代表了有偏差剂量相对于无偏差剂量的偏差百分数,直方图越靠近0,治疗计划的鲁棒性越好。Trofimov等[29]建议使用DVH束去显示不确定因素存在时DVH变化范围,DVH束越宽,说明治疗计划对不确定因素越敏感,鲁棒性越差。Liu等[30]在计划对比时先计算每个体元的均方根剂量(Root-Mean-Square Dose,RMSD),用RMSD体积直方图曲线下的面积(Area Under the RMSD-Volume Histogram Curves,AUC)来对比计划的鲁棒性,AUC越小,代表治疗计划的鲁棒性越好。
目前,虽然商用的治疗计划系统中已集成了DVH束的评估功能,DVH束在临床中也已有广泛的应用,但是国际上还没有可以定量评价IMPT治疗计划鲁棒性的标准,这也就意味着急需找到一种通用且能定量评估IMPT计划鲁棒性的方式,否则有可能会选择一个表面上DVH参数满足要求,而鲁棒性较差的治疗计划。
3 、讨论
与基于PTV优化的计划相比,鲁棒性优化不但提高了治疗计划的鲁棒性,还减少了正常组织的受照剂量[30,31],产生这种现象的原因主要有以下几个方面:(1)鲁棒性优化使得靶区的剂量更均匀,这一点可以尽量保证在有不确定因素存在时的靶区剂量覆盖;(2)常规优化处方剂量覆盖PTV,而鲁棒性优化处方剂量覆盖有偏差情形下的CTV,PTV的体积大于CTV,所以鲁棒性优化可以更好的保护正常组织。不过需要特别提示的是,现在IMPT和IMRT的剂量学对比多是基于等剂量线和DVH参数,这种静态的比较忽略了IMPT对不确定因素的敏感性,在一定程度上会高估IMPT的剂量优势[32,33]。
分次照射过程中的器官运动会导致患者解剖结构形状或位置的改变,进而影响剂量分布[7,34],尽管鲁棒性优化没有直接考虑器官运动以及器官形变产生的剂量不确定性,但是有研究显示由呼吸运动和器官形变造成的照射剂量变差问题能通过鲁棒性优化减小。Liu等[35]研究了9例肺癌患者,通过4DCT考虑呼吸运动,把基于PTV优化的计划与最差剂量优化计划对比,对于靶区剂量,采用最差剂量优化的计划的鲁棒性优于常规计划。Li等[36]对比了9例肺癌患者的常规计划和鲁棒性计划,也得到了相似的结果。但是,需要注意的是,对于肺癌,采用只考虑了射程偏差和摆位偏差的鲁棒性优化治疗计划,在多个分次照射过程中的剂量偏差仍然较大,也就是要解决分次间或分次中由于器官运动或密度变化导致的剂量不一致问题仅依靠考虑了射程偏差和摆位偏差的鲁棒性优化是不够的,还需要制定自适应计划[37]或者采用多CT优化[25,26,27]。目前,多CT优化还处于研究阶段,未见商用计划系统中集成此项功能。
逆向优化的结果取决于设定的优化参数。鲁棒性优化虽然能够提高治疗计划的鲁棒性,但是,要实现一个在无偏差计划质量和鲁棒性之间平衡很好的计划,必须慎重地选择射程和摆位的偏差。不同的质子治疗中心,射程偏差的取值比较一致,通常为3.5%,摆位偏差随照射部位的不同而不同,通常头颈部取3 mm,胸腹部取5 mm[38,39]。
鲁棒性优化的计划质量取决于多个因素,除上述不同的优化算法和优化参数之外,射束方向也会影响治疗计划的鲁棒性。Cao等[40]选择了3例前列腺癌和两例颅底脊索瘤患者,通过与常规平行对穿野对比,无论在无偏差剂量分布还是在存在不确定因素的剂量分布中,射野角度优化后的治疗计划都能很好的保护危及器官。Gu等[41]研究了一种新的IMPT框架,该框架集成了射束方向优化功能(Beam Orientation Optimization,BOO)和通量图优化功能(Fluence Map Optimization,FMO),研究发现,使用BOO-FMO方法产生的射束在射程方面的鲁棒性优于手动设定的射束,摆位方面的鲁棒性也得以保留或改善。
综上所述,鲁棒性优化过程中考虑了射程偏差、摆位偏差和解剖结构改变对IMPT计划的影响。与常规基于PTV优化的IMPT计划相比,鲁棒性优化不但提高了治疗计划的鲁棒性,还减小了危及器官的照射剂量,因此在临床中应使用鲁棒性优化设计IMPT计划。在评估IMPT计划时,应考虑其鲁棒性,虽然目前DVH束是最常用的评估治疗计划鲁棒性的方法,但是,DVH束不能反映IMPT计划对解剖改变的鲁棒性,因此,还急需建立一个简单易用并能被广泛接受的鲁棒性评估方法,方便IMPT计划的对比和评估。
参考文献
[1] ZHANG X D, LI Y P, PAN X N, et al. Intensity-modulated proton therapy reduces the dose to normal tissue compared with intensitymodulated radiation therapy or passive scattering proton therapy and enables inpidualized radical radiotherapy for extensive stage IIIB non-small-cell lung cancer:a virtual clinical study[J]. Int J Radiat Oncol Biol Phys, 2010, 77(2):357-366.
[2] STUSCHKE M, KAISER A, P?TTGEN C, et al. Potentials of robust intensity modulated scanning proton plans for locally advanced lung cancer in comparison to intensity modulated photon plans[J].Radiother Oncol, 2012, 104(1):45-51.
[3] SCHWARZ M, PIERELLI A, FIORINO C, et al. Helical tomotherapy and intensity modulated proton therapy in the treatment of early stage prostate cancer:a treatment planning comparison[J]. Radiother Oncol,2011, 98(1):74-80.
[4] DING X F, LI X Q, QIN A, et al. Have we reached proton beam therapy dosimetric limitations?-A novel robust, delivery-efficient and continuous spot-scanning proton arc(SPArc)therapy is to improve the dosimetric outcome in treating prostate cancer[J]. Acta Oncol, 2018,57(3):435-437.
[5] SZETO Y Z, WITTE M G, VAN KRANEN S R, et al. Effects of anatomical changes on pencil beam scanning proton plans in locally advanced NSCLC patients[J]. Radiother Oncol, 2016, 120(2):286-292.
[6] LOMAX A J. Intensity modulated proton therapy and its sensitivity to treatment uncertainties 1:the potential effects of calculational uncertainties[J]. Phys Med Biol, 2008, 53(4):1027-1042.
[7] LOMAX A J. Intensity modulated proton therapy and its sensitivity to treatment uncertainties 2:the potential effects of inter-fraction and inter-field motions[J]. Phys Med Biol, 2008, 53(4):1043-1056.
[8] LIU W, ZHANG X D, LI Y P, et al. Robust optimization of intensity modulated proton therapy[J]. Med Phys, 2012, 39(2):1079-1091.
[9] ENGELSMAN M, KOOY H M. Target volume dose considerations in proton beam treatment planning for lung tumors[J]. Med Phys,2005, 32(12):3549-3557.
[10]UNKELBACH J, ALBER M, BANGERT M, et al. Robust radiotherapy planning[J]. Phys Med Biol, 2018, 63(22):22TR02.
[11]UNKELBACH J, PAGANETTI H. Robust proton treatment planning:physical and biological optimization[J]. Semin Radiat Oncol, 2018,28(2):88-96.
[12]ALBERTINI F, HUG E B, LOMAX A J. Is it necessary to plan with safety margins for actively scanned proton therapy?[J]. Phys Med Biol, 2011, 56(14):4399-4413.
[13]ZHU X R, POENISCH F, LI H, et al. A single-field integrated boost treatment planning technique for spot scanning proton therapy[J].Radiat Oncol, 2014, 9:202.
[14]QUAN E M, LIU W, WU R, et al. Preliminary evaluation of multifield and single-field optimization for the treatment planning of spotscanning proton therapy of head and neck cancer[J]. Med Phys, 2013,40(8):081709
[15]UNKELBACH J, CHAN T C, BORTFELD T. Accounting for range uncertainties in the optimization of intensity modulated proton therapy[J]. Phys Med Biol, 2007, 52(10):2755-2773.
[16]UNKELBACH J, BORTFELD T, MARTIN B C, et al. Reducing the sensitivity of IMPT treatment plans to setup errors and range uncertainties via probabilistic treatment planning[J]. Med Phys, 2009,36(1):149-163.
[17]PFLUGFELDER D, WILKENS J J, OELFKE U. Worst case optimization:a method to account for uncertainties in the optimization of intensity modulated proton therapy[J]. Phys Med Biol, 2008, 53(6):1689-1700.
[18]LOMAX A J, PEDRONI E, RUTZ H, et al. The clinical potential of intensity modulated proton therapy[J]. Z Med Phys, 2004, 14(3):147-152.
[19]LI Y P, NIEMELA P, LIAO L, et al. Selective robust optimization:a new intensity-modulated proton therapy optimization strategy[J]. Med Phys, 2015, 42(8):4840-4847.
[20]BAI X M, LIM G, GROSSHANS D, et al. Robust optimization to reduce the impact of biological effect variation from physical uncertainties in intensity-modulated proton therapy[J]. Phys Med Biol, 2019, 64(2):025004.
[21]FREDRIKSSON A, FORSGREN A, HARDEMARK B. Minimax optimization for handling range and setup uncertainties in proton therapy[J]. Med Phys, 2011, 38(3):1672-1684.
[22]FREDRIKSSON A. A characterization of robust radiation therapy treatment planning methods-from expected value to worst case optimization[J]. Med Phys, 2012, 39(8):5169-5181.
[23]INANIWA T, KANEMATSU N, FURUKAWA T, et al. Optimization algorithm for overlapping-field plans of scanned ion beam therapy with reduced sensitivity to range and setup uncertainties[J]. Phys Med Biol, 2011, 56(6):1653-1669.
[24]INANIWA T, KANEMATSU N, FURUKAWA T, et al. A robust algorithm of intensity modulated proton therapy for critical tissue sparing and target coverage[J]. Phys Med Biol, 2011, 56(15):4749-4770.
[25]VAN DE WATER S, ALBERTINI F, WEBER D C, et al. Anatomical robust optimization to account for nasal cavity filling variation during intensity-modulated proton therapy:a comparison with conventional and adaptive planning strategies[J]. Phys Med Biol, 2018, 63(2):025020
[26]WANG X L, LI H, ZHU X R, et al. Multiple-CT optimization of intensity-modulated proton therapy-Is it possible to eliminate adaptive planning?[J]. Radiother Oncol, 2018, 128(1):167-173.
[27] CUBILLOS-MES?AS M, TROOST E G C, LOHAUS F, et al.Including anatomical variations in robust optimization for head and neck proton therapy can reduce the need of adaptation[J]. Radiother Oncol, 2019, 131:127-134.
[28]ENGWALL E, FREDRIKSSON A, GLIMELIUS L. 4D robust optimization including uncertainties in time structures can reduce the interplay effect in proton pencil beam scanning radiation therapy[J].Med Phys, 2018, 45:4020-4029.
[29]TROFIMOV A, UNKELBACH J, DELANEY T F, et al. Visualization of a variety of possible dosimetric outcomes in radiation therapy using dose-volume histogram bands[J]. Pract Radiat Oncol, 2012, 2(3):164-171.
[30]LIU W, FRANK S J, LI X Q, et al. Effectiveness of robust optimization in intensity-modulated proton therapy planning for head and neck cancers[J]. Med Phys, 2013, 40(5):051711.
[31]LIU W, LI Y P, LI X Q, et al. Influence of robust optimization in intensity-modulated proton therapy with different dose delivery techniques[J]. Med Phys, 2012, 39(6):3089-3101.
[32]HAMMING-VRIEZE O, DEPAUW N, CRAFT D L, et al. Impact of setup and range uncertainties on TCP and NTCP following VMAT or IMPT of oropharyngeal cancer patients[J]. Phys Med Biol, 2019, 64(9):095001.
[33]GODDARD L C, BRODIN N P, BODNER W R, et al. Comparing photon and proton based hypofractioned sbrt for prostate cancer accounting for robustness and realistic treatment deliverability[J]. Br J Radiol, 2018, 91(1085):20180010.
[34]BERT C, DURANTE M. Motion in radiotherapy:particle therapy[J].Phys Med Biol, 2011, 56(16):R113-144.
[35]LIU W, LIAO Z X, SCHILD S E, et al. Impact of respiratory motion on worst-case scenario optimized intensity modulated proton therapy for lung cancers[J]. Pract Radiat Oncol, 2015, 5(2):e77-86.
[36]LI H, ZHANG X D, PARK P, et al. Robust optimization in intensitymodulated proton therapy to account for anatomy changes in lung cancer patients[J]. Radiother Oncol, 2015, 114(3):367-372.
[37]HOFFMANN L, ALBER M, JENSEN M F, et al. Adaptation is mandatory for intensity modulated proton therapy of advanced lung cancer to ensure target coverage[J]. Radiother Oncol, 2017, 122(3):400-405.
[38]MOHAN R, DAS I J, LING C C. Empowering intensity modulated proton therapy through physics and technology:an overview[J]. Int J Radiat Oncol Biol Phys, 2017, 99(2):304-316.
[39]CHANG J Y, ZHANG X D, KNOPF A, et al. Consensus guidelines for implementing pencil beam scanning proton therapy for thoracic malignancies on behalf of PTCOG thoracic and lymphoma subcommittee[J]. Int J Radiat Oncol Biol Phys, 2017, 99(1):41-50.
[40]CAO W H, LIM G J, LEE A, et al. Uncertainty incorporated beam angle optimization for IMPT treatment planning[J]. Med Phys, 2012,39(8):5248-5256.
[41] GU W B, NEPH R, RUAN D, et al. Robust beam orientation optimization for intensity-modulated proton therapy[J]. Med Phys,2019, 46(8):3356-3370.





