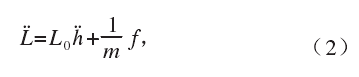在现有的引力理论中,广义相对论是能通过到目前为止所有引力实验检验的、最为简洁的引力理论之一。下面由学术堂为大家整理出一篇题目为“引力波探测相关研究综述”的天文学论文,供大家参考。
原标题:引力波探测和引力波天文学
一、引力波理论基础
引力相互作用是目前人类已经认识的四种基本相互作用之一。广义相对论是爱因斯坦在1915年提出的引力理论。在现有的引力理论中,广义相对论是能通过到目前为止所有引力实验检验的、最为简洁的引力理论之一。光线偏折、时间延迟、引力红移、黑洞等广义相对论的理论预言一一被实验所证实。引力波也是广义相对论的重要理论预言之一。泰勒(J. Taylor)和赫尔斯(R. Hulse)通过对双星系统PSR1913+16的观测间接证明了引力波的存在,他们也因此获得1993年的诺贝尔物理学奖。但直到现在人们还没有直接观测到引力波。
现存的几乎所有引力理论都预言了引力波的存在。下面我们介绍广义相对论对引力波的理论描述。在广义相对论中,引力由时空几何来描述,引力波也就对应时空几何的波动。在时空中除引力外不受力的测试粒子沿测地线运动。测地线对应我们常见的欧氏几何中的直线。没有引力存在的时空对应的几何是最简单的非欧几何--闵氏几何,其上的测地线也是直线。引力的存在将导致时空的弯曲,这时的几何将是复杂的非欧几何,其上的测地线也变成复杂的曲线。通常我们把时空中除引力外不受力的粒子叫做测试粒子。两个相邻的测试粒子各自沿时空的测地线运动,当时空几何发生波动时,它们之间的距离也随之发生波动。该过程定量地由测地偏离方程描述(感兴趣的读者请参阅梁灿彬、周彬所着《微分几何入门与广义相对论》,上册公式7-6-8)。
通常,在探测引力波的时空区域,引力场很弱,可以用微扰的办法来描述引力波。在该方法中,引力波由一个量纲为1(或者说没有单位)的量h来描述。假设没有引力波时上述的两个沿测地线运动的测试粒子间距L0,引力波来了后它们的距离变为
在发射引力波的源端,引力场很强,近似理论一般都失效。引力波在源端的行为分为近场区和波动区如同电磁波的发射一样,在近场区,波的概念不清楚。人们更关心的是波动区的行为。对于引力波源,波动区在理论上对应为引力波源作为孤立体的渐近区。在渐近平直时空的情况下,这个渐近区可以用邦迪-萨克斯理论框架来描述。在该框架下,引力波描述为消息函数c。其
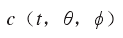
中的θ和Φ是球坐标系的角度坐标。消息函数c对应上述h的一阶时间导数
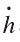
。
再根据(1)可知,邦迪消息函数的一阶时间导数对应测试粒子的相对加速度。从以上的讨论可见,引力波的行为归根结底就是时空几何的行为。但这里的描述只是运动学层次的描述。动力学描述涉及爱因斯坦方程的求解,我们将在第四节中讨论。
二、引力波探测器
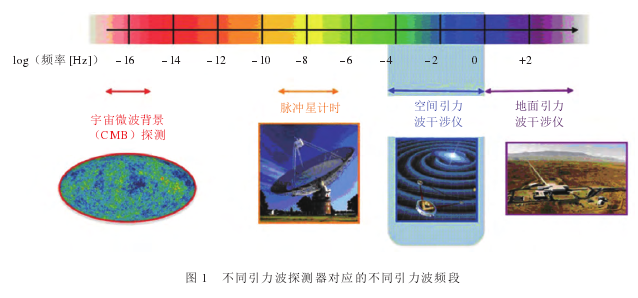
通过测量引力波对物质的影响即可探测引力波。目前人们有以下五种引力波探测方式。在宇宙早期,引力波对电磁辐射产生影响。这些电磁辐射演化到今天变成宇宙微波背景辐射(CMB)。通过对CMB的相关测量可测量宇宙早期的引力波,这样的探测器包括BICEP等。宇宙中的星体,如脉冲星、地球等,近似地是孤立系统,所以沿测地线运动。通过测量脉冲星与地球间的距离变化即可测出测地偏离,从而达到测量引力波的目的。脉冲星计时测量就是这样的测量方式。通过悬挂或者无拖拽等先进技术让试探物体沿测地线运动,同时通过激光干涉测量试探物体间的距离变化也可达到引力波测量的目的。正在运行的LIGO等地面干涉仪和计划中的空间引力波探测计划e LISA和天琴等使用的就是这样的探测方式。引力波和物体相互作用,在适当的情况下可以导致物体共振,韦伯型共振棒就是通过这种方式测量引力波的。通过测量引力波对高斯型微波光子流的影响也可以达到引力波探测的目的。微波频带高频引力波探测器使用的就是这样的测量方式。从实际探测的角度看,这些探测器具有不同的测量频段(如图1所示)。
CMB探测的引力波频段在约10-16Hz,脉冲星计时探测的频段在约10-8Hz,空间引力波干涉仪的探测频段在约0.01Hz,地面引力波干涉仪以及韦伯型共振棒的探测频段在约几百Hz,高斯型微波光子流探测器的频段在约109Hz.
在引力波探测实验中,方程(1)动态地表现为
其中L是两个试探物体的距离,L0是引力波不存在时两个试探物体的距离,m是试探物体的质量,f是试探物体所受的除引力外的作用力。为了提高实验灵敏度,f要做得尽量的小,这就是LIGO复杂悬挂系统的动机。理想地,f =0,方程(2)的解可写为
可见引力波可导致测试物体间的距离变化ΔL=L0h.引力波探测器的灵敏度体现为能分辨的最小h大小。随着人类精密测量技术的发展,引力波探测器的测量精度也越来越高。典型地,当前LIGO的测量精度约为10-22,脉冲星计时的测量精度约为10-15.在不久的将来,LIGO升级到Advanced LIGO,精度可达10-23;等到平方公里阵列望远镜(SKA)建成,脉冲星计时的测量精度可达10-16.考虑到LIGO的测试物体间距约4千米,h≈10-23的测量精度意味着它可以测量出ΔL=L0h≈10-20米的距离变化。这比原子核的直径10-15米还要小5个数量级!


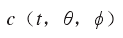 中的θ和Φ是球坐标系的角度坐标。消息函数c对应上述h的一阶时间导数
中的θ和Φ是球坐标系的角度坐标。消息函数c对应上述h的一阶时间导数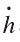 。
。