摘要:从事件间的关系与运算,事件概率的计算以及互不相容,相互对立,相互独立的理解与区分三个方面,阐述数形结合思想运用到概率论的教学中,利用韦恩图,形象高效地提高教学效果。
关键词:韦恩图; 事件间的关系; 概率的计算;
Abstract:From three aspects: the relationship and operation of events, the calculation of event probability, mutual incompatibility, mutual opposition, and mutual independent understanding and distinction, this paper expounds the application of the idea of combination of number and shape in the teaching of probability theory and the use of Wayne diagram to improve the teaching effect vividly and efficiently.
Keyword:Wayne diagram; relationship between events; calculation of probability

0 引言
概率论是一门研究随机现象的统计规律的数学学科,随着现代科学技术的发展,概率论在自然科学、社会科学、经济管理等领域得到了越来越广泛的应用。而概率论又是统计学的理论基础,也是理论性比较强的一门课程,初学者学习这门课程时,感觉知识点多,定理晦涩难懂,公式繁杂,解决实际问题时没有头绪。
借助数形结合的思想,在课堂教学中引入韦恩图,不但可以形象、直观地解释公式和定理,使学生容易理解知识点并记住公式,而且在引导学生解决问题时借助韦恩图也可以开拓学生思路,将问题难度大大降低。这样不仅能提高教学效果和效率,还可以增加学生自信和学习概率论的兴趣。本文总结多年财经类院校教学的经验,探讨了韦恩图辅助概率论教学的方法,以提高教学的效果。
1 韦恩图表示事件间的关系和运算
在中学数学中,集合的表示方式有三种:列举法、特征法和韦恩图。借助图形可以表示集合以及集合之间的关系运算,也可以帮助学生理解运算律和解决集合问题。
在概率论的开篇,随机试验的一切可能基本结果组成的集合称为样本空间,就是引入了集合这一数学工具来表示样本空间,而任意一个随机事件都是样本空间的子集,所以随机事件其实也是集合。那么事件也有三种表示方式,而图形的表示方式可以很形象直观地帮助解释理论,将繁杂、抽象的公式或者定理简明、清楚地展示给学生,加深学生地理解和记忆,大大地提高教学效率。
韦恩图表示事件间的关系与运算如图1.
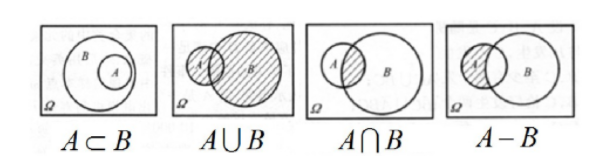
图1 韦恩图
2 韦恩图辅助求解抽象的事件的概率问题
随机事件的概率计算是概率论教学中的一个重点和难点,抽象的事件的概率计算又是其中重要组成部分。抽象的事件的概率计算问题是指,并未给出随机试验的具体内容,仅给出事件的符号和关系,需要学生运用概率的定义和性质来计算问题事件的概率。如果只依靠公式推导,学生很难理解,也很难掌握求解方法。但是利用韦恩图的话,可以很容易使学生看到事件的关系,并且找出求解概率的方法。
首先,做一个一一映射,将样本空间的矩形的面积对应为样本空间(必然事件)的概率P(Ω)=1,那么任意事件A的图形的面积也就对应此事件的概率P(A)。
例1:设A、B为两事件。

图2 例1韦恩图
上述方法1是直接利用公式进行逻辑分析,再进一步运算,涉及很多公式,而方法2则利用图形很简洁清楚地表示出问题事件与已知事件之间的关系,只利用一个减法公式即可得出结果。明显,方法2可以使学生容易明白并掌握。
例2:设A,B为两事件。

图3 例2韦恩图
3 借助韦恩图区分几个重要的事件间的关系
在概率论中,事件之间的三种关系:互不相容、相互对立和相互独立,是很重要的内容,也是实际应用中很重要的三种特殊关系。但是他们三者之间不容易区分,学生很容易混淆,以至于乱用公式,导致无法解决问题。这里利用韦恩图来表示和区分它们三者,也能达到简单直观和明确无误的教学目的。
当P(A)>0,P(B)>0时,事件间的三种特殊关系:图4表示事件A与B互不相容,图5表示事件A与B相互对立,图6表示事件A与B相互独立。这里强调事件发生当且仅当此事件(也是集合)中一个元素出现。
从图4、图5、图6中很容易看出:互不相容等价于:AB=Φ;相互对立等价于:AB=Φ,并且A∪B=Ω。两个事件A与B互不相容,若A发生则B必不发生,若A不发生则B不一定发生。而相互对立的两个事件A与B,若A发生则B必不发生,若A不发生则B一定发生。
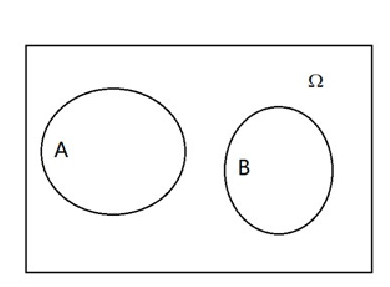
图4 事件A与B互不相容
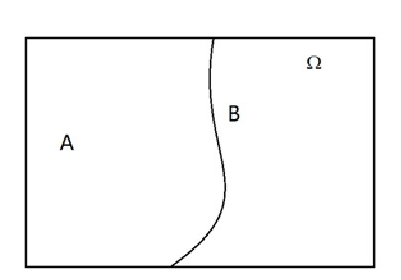
图5 事件A与B相互对立
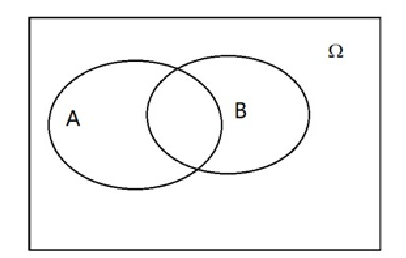
图6 表示事件A与B相互独立
另外,通过图形可以很容易使学生明白它们三者的区别,做出下列判断:当P(A)>0,P(B)>0时,互不相容的两个事件不一定相互对立;相互对立的两个事件一定互不相容;互不相容的两个事件一定不独立;相互独立的两个事件一定不是互不相容的;相互对立的两个事件一定不独立;相互独立的两个事件一定不是相互对立。这些关系的联系和区别看似错综复杂,但是通过韦恩图,就可以清晰地给学生讲解明白,学生也能拨开迷雾,做到真正理解和运用。
4 结语
数形结合的思想运用到概率论的教学中,可很大程度提高教学的效率,用韦恩图形象地表示事件以及概率,可以使学生更容易准确地理解公式等理论,还能使学生将韦恩图作为工具,在解决问题时降低难度,提高学生兴趣和主动性。所以,韦恩图在概率论其他方面的教学中的应用值得进一步探讨和广泛地应用。
参考文献
[1]盛骤,谢式千,潘承毅。概率论与数理统计[M].北京:高等教育出版社,2008.
[2]毕学慧,刘华明,倪扬眉。韦恩图在概率论中的应用[J].福建电脑,2017,33(07):10-11+75.
[3]庞帮艳,于晓要。韦恩图在概率论中的妙用[J].漯河职业技术学院学报,2010,9(05):60-61.
[4]张厚品。韦恩图的起源[J].数学教学,2005(07):48-49.
[5]辜纯健。韦恩图在概率计算中的应用[J].湖南环境生物职业技术学院学报,2004(04):369-371.
[6]高慧明。韦恩图在集合运算中的妙用[J].数学通讯,2004(18):12-13.
[7]单文海,沈国兴。集合单元要重视韦恩图的教学功能[J].数学通报,1997(07):13-15.





