
1 控制特性检测数据的准确度
检测数据的准确度应从测量不确定性说起.用同样一把卡尺测量同一工件相同尺寸,多次测量的结果是不一样的.经过前人研究,每次测量结果不是同一值,而是以一定的概率分散在某个区域内的多个值.这个分散程度可以用方差表示.注意这里所说的分散性不是测量误差,更不是测量失误.众所周知,测量误差可以通过后期的修正使误差值很小,小到可以接受的范围之内,几乎接近真值.而这个分散程度的方差或其标准差对于修正后的误差而言则更大一些.
测量不确定度是一个区间,而误差是一个值.系统误差可以修正,而不确定度是无法修正的.而测量的不确定度或者说检测数据的准确度可以由测量误差所引起.
制造业中的质量特性是控制关键,所说的质量特性可以是零件尺寸,或者是总成的性能,抑或是过程的参数……这些质量特性的实际表现往往通过数据来体现.我们假设被测量 Y 与输入量 X 是通过函数关系 Y=(fX)联系的.这里的 f 所代表的是测量程序和评定方法.不同的测量方法 f 是不同的.而工业制造中 X 是随机的,这样在 f 确定的情况下 Y 也是随机的.而根据中心极限定理:多个相互独立随机变量的平均值服从正态分布.所以多次测量的平均数(既样本均值)服从正态分布.
正态分布的均值表示数据集中的位置,而方差或标准差表示分散的程度.关于测量的数据,当然希望均值的估计是无偏的,而方差越小越好.但是由于测量不确定度的原因,使我们无法避免均值和方差的参数估计.通过多次的测量获得大量的数据通过统计学知识来识别测量不确定度,从而获得更理想的数值.
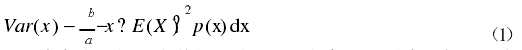
上面给出式 1 的是方差的公式,从公式中可以看出 x 与 E(x)之间的差异决定方差 Var(x)的大小,因为不管正负(样本数据大于平均数或者是样本数据小于平均数)方差始终是正的,这样可以预防不同方向的差异相互抵消.所以单纯从测量数据的方向看,方差是有效的.
2 质量控制方法
资本主义国家工业革命时期,美国的休哈特等人的工作组首先提出了过程控制理论以及控制过程的具体工具---控制图.
直至今日控制图作为大多的生产制造型企业控制质量的有力手段.控制图也是统计过程控制(Statistical Process Control,简称 SPC)的核心知识.SPC 是在生产制造过程中的一种预防性质量管理工具,用来分析过程是否稳定,过程控制是否充分.
控制图中对质量特性控制数据进行了识别和统计.质量特性数据在一定范围内是随机发生的,可以通过两个步骤来对数据进行分析:第一利用控制图分析过程的稳定程度,对过程存在的异常因素进行预警;二是计算过程能力指数分析稳定的过程能力满足技术要求的程度,对过程质量进行评价.质量控制就是通过这两个步骤来发现过程的致病因素,就是产生不合格原因的隐患,从而在产生不合格品之前就修正过程、预防不合格品的产生.
质量特性数据随机取值的规律意味着该特性的数据满足正态分布,这里说的数据应理解为真实零件的实际值而不是测量值.因为前面提到过测量值因为误差的原因是有不确定性的.注意这个值并不是一个理论值,它真实存在只不过你无法通过任何手段无偏的获得.而且它的随机性也无法通过函数关系表示.当然可以通过大量实贱来获得,但考虑到成本和效率这里不做过多的探讨.毕竟我们讨论的是现有生产力水平下的制造业生产,而不是搞科学研究.
既然满足正态分布就有均值和方差,下面以质量常用的工具X-R 图来进行说明.根据中心极限定理,不管自变量 X 服从正态分布还是不服从正态分布,当样本量足够大时,X 始终服从正态分布控制图中有上下限 UCL 和 LCL 一般情况上下限是区分偶然波动和异常波动的界限.产品质量的正常波动是满足正态分布的,根据正态分布的规律中心线向上移动 6σ 作为 UCL 向下移动 6σ 作为LCL.当有异常波动发生的时候,依照时间顺序取点就会发现规律:
要么点落在控制限以外,要么点的排列不正常.这样就发现了不合格征兆,从而采取措施阻止不良趋势的进一步扩大.注意一定要按照时间的顺序描点作图才会有意义,而控制图也是在一段时间内实施控制,所反映的是过程量,不是统计时刻的值而是通过现有质量控制手段所达到的控制结果的一种体现.
过程能力分析控制图中也有 UCL 和 LCL 意义也是相同的.只不过反映的同一时间内一个样本或者几个样本集中分散程度.与控制图相似的是如果数据落在控制限以内合格,落在控制限以外超差.而控制限一般设为零件的公差上下限,这样就可以根据实际数据做参考,通过图形的比较发现不合格的趋势.他的意义是反映过程能力是否充分.数据过于分散图形扁平,有可能超越控制界限产生不合格则过程不稳定.数据虽然集中,但均值距离控制界限过于接近,体现在图形上左右偏倚仍然有风险产生不合格过程也不稳定.稳定的过程是图形集中在中线附近,而且分散程度不足以超越控制界限,甚至距离该界限甚远.只有这样的过程我们才放心,或者说这样的过程不可能生产出不合格品.
学术上有一个好听的名字来描述这个过程能力,叫做过程能力指数:Cp
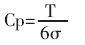
T-公差带宽度;σ-质量特性值分布的总体标准差(方差的平方根)
3 原始数据与统计方法的方差分析
前文提到过的测量不确定性是随机变量满足正态分布,而统计质量中的过程能力也是通过公差带和标注差计算得出.二者之间的共同点就是都运用到了方差分析方法.式 2 方差分析能有有效的防止偏差相互抵消,从而更灵敏的体现数据分散程度.但是制造业生产中质量控制受到时间和成本的制约往往不能将测量不确定度和质量统计过程区分对待.这样就有一个新的问题产生:测量值与真值不符,而统计没有发现,造成误判.误判的结果有两个:要么把假的看做真的,要么把真的看做假的.这个结果是有意义的.有可能错过了预防不良的机会,有可能牺牲过度的成本来控制不必要的质量,有可能造成不合格品的产生.
参考文献
[1]张梦欣.质量专业综合知识[M]北京:中国人事出版社,2012.
[2]张梦欣.质量专业理论与实务[M]北京:中国人事出版社,2012.





