摘 要: 本文在蝴蝶效应理论中引出的混沌系统的基础上, 提出了一种串行忆阻器的混沌系统, 通过建立混沌系统的电路图, 给出电路的关系式, 再通过仿真器去模拟基于此电路的混沌系统。在密码学的发展过程中, 密码变得越发复杂, 解密技术也愈加发达, 信息的保密性开始受到威胁, 在此基础之上, 将混沌的复杂性与无法预测性结合在密码的组合中, 使得密码变得更加多变复杂, 本文中也展现了基于此混沌系统的图像的加密和解密。实验结果表明, 串行忆阻器系统的电路可以产生混沌, 并且混沌系统能对图片进行较好的保密。
关键词: 串行忆阻器和并行忆阻器; 简易混沌电路; 密码学与混沌系统;

0、 引言
在日新月异的现代社会中, 科技更新换代速度很快, 互联网信息输送以及信息传输的隐私性日益重要, 这使得信息的保密与识别显得至关重要。然而说到保密系统, 肯定有人会提起新兴崛起的混沌系统。所谓混沌系统, 最早来自于自然界中变化无常的天气, 由于天气变化这种变化无常, 难以预测的特点, 美国科学家洛伦兹提出了最早的混沌现象, 也就是“蝴蝶效应”, 天气的难以预测性和强烈的无序性, 为混沌的建成提供了理论支持, 但是蝴蝶效应和混沌也存在着明显的差异性。混沌系统的提出来自于蝴蝶系统, 但是公式的导出却来自于数学的公式和推导。随着对这种初始的混沌系统研究的进一步地加深, 科学家们便通过忆阻器电路创造了混沌系统。随着近年来的研究一步步加深, 现在专家已经发现混沌系统有着初始值敏感性和无法预测性等特征, 因而可以作为新型密码应用于信息加密之中, 由于密码容易被预测评估, 导致数据的安全性保密性下降, 由于这种问题的出现, 引出了混沌系统的新型应用。然而密码的难侦破性也来源于数据系统的复杂性与变化性, 在混沌系统研究的一步步深入的情况下, 混沌学崭露头角, 专家发掘了其与密码学的联系, 混沌系统的不确定性以及难以预测性的特点, 完美迎合了密码学的需要, 混沌与密码学也有着相通的特征, 使得密码学与混沌系统结合, 诞生出了一门新型学科—混沌密码学, 混沌密码学的出现进一步地推进了保密技术。
1、 忆阻器
忆阻器全称记忆电阻, 最早是由中国科学家蔡少棠先生于1971年提出的。忆阻器顾名思义, 电阻的变化是有记忆性的, 其效果是电阻会随着通过的电流的变化而变化, 而且假使电流突然消失了, 它的电阻仍然会保留之前的值, 直到受到反向电流才会继续改变。
蔡少棠教授将忆阻器的概念进行拓展, 其定义为:
u (t) 表示输入信号, y (t) 表示输出信号k (·) 表示连续n维的向量函数g (·) 表示连续n维的标量函数, 标量函数与向量函数都与具体器件有关, 输出信号以及输入信号可取电荷、电流、电压和磁通中的任意一种, 当取电荷时即为电荷控制型的忆阻器, 同理则为电压或电流控制型的忆阻器。
在这里我们定义了一个通用的压控忆阻器, 如下:
忆阻器的忆阻值受z影响, 不随着电流变化而变化, 同时表现了z随着电压变化而变化, 体现了此为一个压控忆阻器。其中c, k为调控忆阻器变化的参数, 从而调控系统的性能。
2、 忆阻器混沌电路模型
利用上述的忆阻器, 我们可以构建简单的串行混沌电路图系统。通过添加电容和电感我们得到如图1所示的设计, 在串联的图中我们可以发现iM=iL=iC, 根据电压环路定理我们可以得到基于电容电感忆阻的环路电压方程。
图1 电容电感忆阻电路
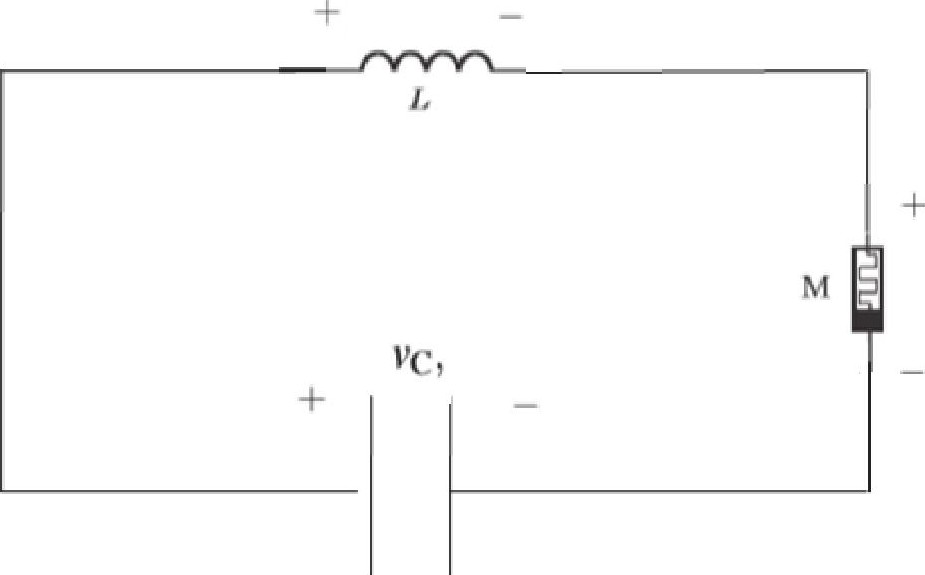
状态方程中中vC和iL分别为经过电容的电压和经过电感的电流。其中参数选择k=1, c=0.5, L=1, C=1, 初始条件为 (0, 0.1, 0) , 利亚诺普指数存在一个或多个大于0, 且利亚诺普指数之和小于0, 维数也为分数维度, 那么说明系统进入的混沌。那么给出如下的归一化方程。
图2 混沌图
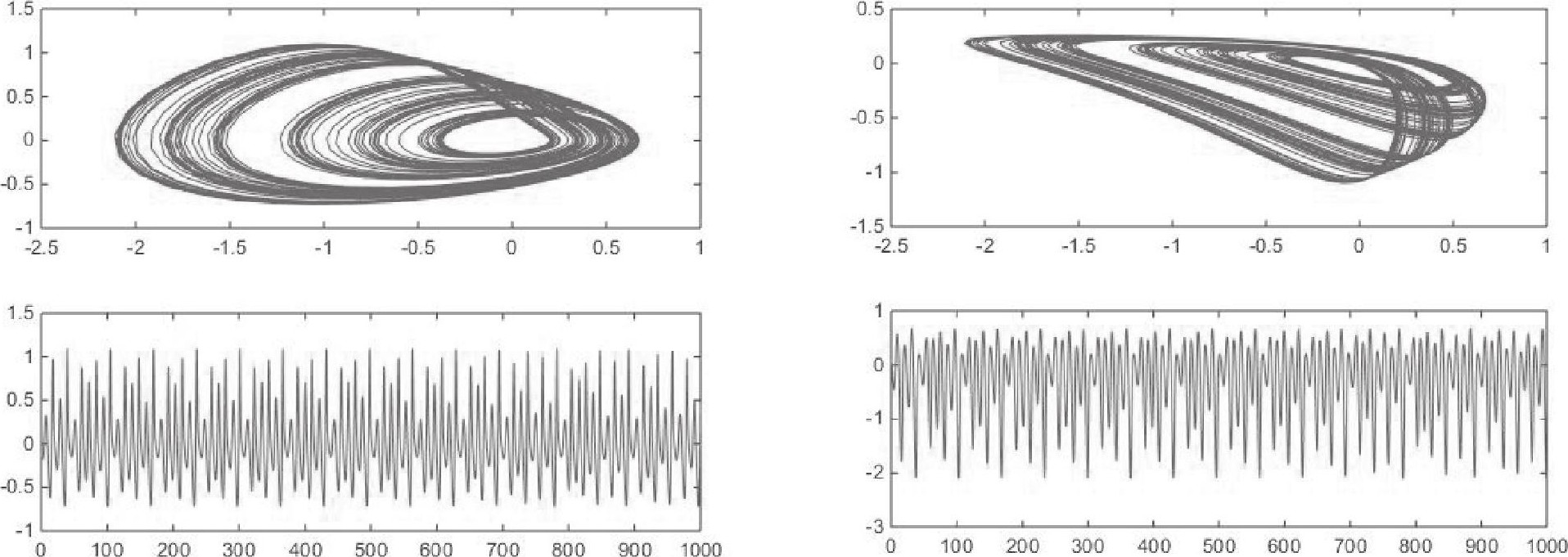
如图2所示, 观察他们的x-y, y-z界面的混沌图, 明显看出图中的吸引子在时间序列上的混沌非周期性
的状态, 平面任何时刻的点都不出现重合
3、 基于混沌的图像加密
混沌序列的获取使得混沌系统在实际应用过程中取得了很好的效果, 得到了一定的肯定, 混沌序列应用到加密过程中会使得信号获得非周期性, 这样的信号很难预测, 因此特别适合保密系统的应用。
忆阻混沌系统对初始条件极为敏感, 密钥空间大, 难以攻破, 所以提取基于忆阻器的混沌序列极其重要。本文采用像素位置置乱变换和像素值替代变换相结合的加密思想, 进行了数字图像加密和解密系统设计。引入了整数域的逆仿射变换, 采用logistic混沌映射结合的方法, 生成了混沌序列, 像素变换和灰度值替换受到混沌序列的影响。这种混沌变化大于普通单一的混沌变化, 具有更强的加密特性, 加密强度较强。如图3所示分别是得到了加密前原始图像、加密后图像以及解密后的图像。
图3 混沌加密图像示意图

4、结论
本文提出了一种仅由忆阻器、电容和电感构成的最简的串行忆阻器混沌系统, 系统存在着复杂的混沌动力学行为, 电路仿真实验结果与数值仿真一致。该系统拓展了对混沌系统、忆阻器混沌系统的研究思路。
参考文献:
[1]田晓波.忆阻器电路特性与应用研究[D].湖南:国防科学技术大学, 2009.
[2]王乐毅.忆阻器研究进展及应用前景[J].电子元件与材料, 2010, 29 (12) :71-74.
[3]许碧荣.一种最简的并行忆阻器混沌系统[J].物理学报, 2013, 62 (19) :91-98.
[4]胡柏林, 王丽丹, 黄艺文, 等.忆阻器Simulink建模和图形用户界面设计[J].西南大学学报 (自然科学版) , 2011, 33 (9) :50-56.
[5]王晓媛, 齐维贵, 王兴元.忆阻器的电路实现及其混沌动力学研究[J].北京航空航天大学学报, 2012, 38 (8) :1080-1084.
[6]方清.基于忆阻器的混沌电路设计[D].湖南:湘潭大学, 2013.
[7]闵富红, 王珠林, 王恩荣, 等.新型忆阻器混沌电路及其在图像加密中的应用[J].电子与信息学报, 2016, 38 (10) :2681-2688.
[8]Chua L O.Memristor-The missing circuit element[J].IEEE Trans Circuit Theory, 1971, 18 (5) :507-519.
[9]Chua L O, Kang S M.Memristive devices and systems[J].Proc IEEE, 1976, 64 (2) :209-223.





