
合理阶段速度分配对长距离竞速类项目运动成绩以及竞赛名次影响较大,在决胜于毫厘之间的当今高水平竞赛中,其更是一个关键制胜因素。在该类项目优秀运动员训练和比赛中,合理分配阶段速度被作为一个常用的训练、监控目标,也是战术制定的基本依据。因此,对于合理专项速度分配特征探索显的尤为重要。
函数型主成分方法是 1 种以函数为单位的降维方法,能够探索函数型数据的变异性,如主要曲线变异形式、典型曲线类型等[1]。由于该方法依赖较少的假设条件和较弱的结构约束,极其适合于分析时间序列数据,其应用越来越广泛[2]。本研究中,以孙杨为个案,将其阶段泳速、划幅及划频曲线整体作为分析对象( 函数) ,应用函数型主成分方法将其多次 1 500 m 自由泳比赛中这些参数曲线间的波动进行降维处理,进而展开分析,藉此一方面探讨函数型主成分方法在速度节奏或速度分配量化诊断、监控以及研究中的适用性,另一方面探讨1 500 m 自由游中优秀运动员泳速及其相关参数的波动规律以及合理分配特征,旨在为 1 500 m 自由泳运动员速度节奏的诊断提供一种新方法以及为其科学训练、战术制定提供科学依据。
1 研究方法
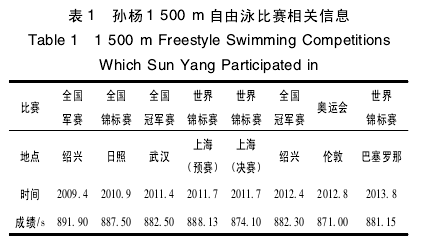
1. 1 样本 以国内外 8 场 1 500 m 自由游泳比赛中孙杨游泳技术动作作为研究样本。如表 1 所示,在这些比赛中,孙杨均取得了冠军,依运动成绩判断均发挥正常。【1】
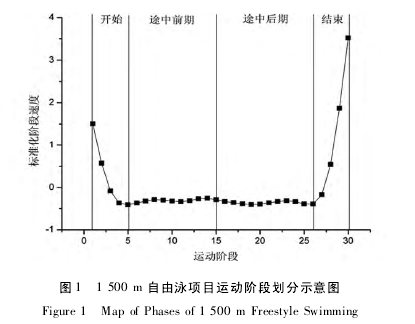
1. 2 运动阶段划分 依据 1 500 m 自由泳中泳速的变化特征( 图 1) ,将 1 500 m 自由泳项目运动过程划分成开始、途中和结束 3 个阶段,其中途中阶段被均分成途中前期与后期。开始阶段为 0 ~250 m,此时平均阶段速度呈现大幅度下降,直到最低水平; 途中阶段为 250 ~1 250 m,此时平均阶段速度基本上维持在开始阶段结束时的水平; 结束阶段为 1 250 ~1 500 m,此时平均阶段速度呈现急剧上升,直到最高水平。【2】
1. 3 指标及测量 通过影像拍摄与解析对孙杨比赛中阶段泳速、划距以及划频3 个指标进行测量。由国家队或浙江省队科研人员对比赛中孙杨游泳技术进行拍摄与分析,机位设置等细节详见温宇红、周晓东等论文说明[3 -4]。划频指几个完整动作所需时间换算成每分钟动作次数,单位: 次/ 分; 游速指某段距离除以运动员头部通过该段距离时间,单位: m/s; 划幅由划频及速度推算出平均每次动作前行的距离,单位: m/次。
1. 4 函数型主成分基本原理 函数型主成分方法是指采用函数型数据计算原理对具有函数特征的指标进行分解、降维。其基本原理是通过求解函数型指标变量协方差矩阵方程的特征函数( ξ( t) ) ,从而计算函数型主成分的权重函数( w( t) ) 以及函数型指标变量在这些主成分中的得分( c )[5]。
函数型指标变量协方差矩阵方程的特征函数求解如下:【3】

1. 5 函数型主成分分析过程 首先,为了尽量消弱不同场次比赛中机能储备、机体状态等因素对阶段泳速及其相关参数曲线形态可比性的影响,将阶段速度、划距与划频进行了标准化处理。随后,采用 30 个 4 阶 2 次样条基函数,设置平滑参数为 1,将标准化后的参数拟合成函数。最后,对各 8 次标准化阶段速度、划距以及划频函数间波动进行降维,获得其几种主要的波动形式( 主成分) 。主成分数量的确定标准为要求累积贡献率达到85%以上,最低主成分的贡献率达到 10%以上,以确保各主成分包含足够的信息量。其中,权重系数与得分是该方法中2 个重要统计量,前者表示了众多函数曲线间的波动形式,后者则代表每个函数曲线在各主成分中的典型形态。函数型数据分析过程中所有计算均在Matlab7. 0 软件中通过编程实现。
1. 6 数理统计 采用皮尔逊相关分析方法计算多次比赛中速度、划距、划频节奏在通过函数型主成分分析后获得的主成分中得分与运动成绩的相关系数,并进行相关系数的显着性检验。使用 Excel、Origin8. 0、Spss17. 0 软件完成全部的数据处理以及制图。
2 研究结果
通过函数型主成分分析后得出,孙杨多次竞赛间阶段泳速、划距与划频曲线波动各自均可降维成 3 种主要成分,代表了 3 种主要波动形式。这些主成分累积贡献率分别为 92%、90% 以及 95%,其中主成分 1贡献率分别为 69%、46%、44%,主成分 2 贡献率分别为 13%、24%、35%,主成分 3 贡献率分别为 10%、19% 、16% 。可见,这些主成分累积贡献率均在 90%以上,最低主成分贡献率也在 10% 以上,这显示 3 种主要波动形式基本上囊括了这些参数曲线全部的变异性,并且,每种主要波动形式具有足够的代表性。
通过相关分析得到,第1、2 主成分上阶段泳速、划距、划频得分与运动成绩间相关性都低于 0. 5,经检验不具显着性; 然而,在第 3 主成分上阶段泳速、划距、划频得分与运动成绩具有显着性相关,相关系数依次为 0. 68、-0. 78、0. 82( 图 2 中 A1、B1、C1) 。这说明只有第 3 主成分中阶段泳速、划距、划频的波动形式对运动成绩有影响。从图 2 中 A2、B2、C2 中进一步可见,阶段泳速、划距、划频各自第 3 主成分中的波动度绝对值居前 2 位的都是途中前段和结束阶段,其中后者较高,并且变化方向相反( 图 2 中“-”表示波动负方向; “+ ”表示波动负方向) ,这体现出该主成分中这些参数曲线的波动形式主要特征为“途中前期-结束”阶段间非线性互补波动。图 2 A2、B2、C2 又展示了在第3 主成分中得分较高、间高度关联,因此这也代表了运动成绩较好( 图 2 中“HP”) 、较差( 图 2 中“LP”) 时这些参数的曲线形态。从中可见,运动成绩较低时这些参数曲线形态,基于其得分与运动成绩较好时,泳速与划频在途中前段中倾向于较高,在结束阶段中则相反; 划距在途中前段中倾向于较低,在结束阶段中则相反。
3 讨 论
在长距离竞速类项目中,阶段速度分配合理与否对高水平竞赛中取得优异成绩或名次具有重要作用,一直被教练员、运动员以及相关领域科研人员所关注。本研究采用函数型主成分方法对孙杨多次 1 500 m 自由泳竞赛中阶段泳速及其决定因素的波动进行降维,并展开分析,藉此不仅探寻这些参数曲线的波动规律以及合理的阶段配比特征,而且探讨函数型主成分方法在速度节奏诊断、优化、监控以及研究中的适用性。
1 500 m 自由泳中,优秀运动员阶段泳速分配具有类似的“抛物线”模式[6],即在开始与结束阶段较高,途中阶段较低。多个运动员 1 次竞赛间或 1 个运动员多次竞赛间阶段泳速分配存在一定的波动,即以上述基本模式为基准上下起伏。作为阶段泳速的决定因素,阶段划距与划频变化也是如此。本研究中显示,多次 1 500 m 自由泳竞赛中优秀运动员阶段泳速、划距以及划频曲线的波动分别可通过函数型主成分方法被降维成 3 种主要波动形式,呈现出 3 种围绕着均值参数曲线上下起伏形式,其中第 3 种波动形式对运动成绩有明显影响。这些参数曲线间的波动可能由不同机能分配模式及其执行程度、战术安排及其执行程度、心理状态、机能状态以及技术发挥程度等之中的单个或多个因素作用所致,从而对运动成绩产生影响。近年来,已经在赛跑[7]、游泳[8]、竞走[9]、速度滑冰[10]、赛艇[11]、皮划艇[12]等众多项目中对优秀运动员阶段速度分配与其专项运动成绩提升间的关联予以探索,绝大多数研究显示,这 2 者间存在密切关联,合理速度分配能够促进其专项运动成绩的提升。本研究基于函数型主成分分析方法,从一个新视角展示了 1 500 m 自由泳中阶段泳速以及相关参数曲线间波动形式与运动成绩间的关联。
这类研究中,不仅仅是揭示阶段速度分配与运动成绩间的关联,更重要的是探讨合理的专项阶段速度分配特征。本研究中显示,各次 1 500 m 自由泳中阶段泳速及其决定因素曲线间第 3 种波动形式呈现出“途中前-1在途中前段倾向于较低,在结束阶段中则相反。从中可见,当运动成绩较好时,泳速在途中前段下降较少,在结束阶段提高同样较少,全程变化较小( 图 2A2 中反映更直观) 。这与 Brown 等[13]的研究结果较为相似,发现在同属于长距离竞速类的2 000 m赛艇项目中,相对低级别运动员而言,国际级选手艇速在500 ~1 500 m 间降幅与1 500 ~2 000 m 间增幅较低,全程变化较小。相对较小的全程阶段速度变化被认为更加节省能量,有助于较好运动成绩的取得[14]。
此外,该项目中泳速在途中前段较高,在结束阶段较低,是一种良好竞赛策略或机能分配模式的表现。据文献[15]报道,在30 届奥运会上该项目在 400 ~1 500 m 间每隔 50 m 的名次排位改变就很小了。也有文献[6]报道,这段距离区间内每隔 100 m 处成绩与最终运动成绩均具有高度关联,这同样体现了该距离区间内排名变动不大。这说明在该距离区间之前或是其前期( 途中前段就在其中) 争夺 1 个较好的排名对最终运动成绩或名次帮助甚大,这可归因为:1) 可以获得较好的心理优势; 2) 避免对手干扰,控制好自身运动节奏;3) 尽量避免在随后追赶中更多的能量耗费与运动疲劳积累的影响。同样,在结束阶段中,运动员之间距离已经被拉开到一定程度,又由于运动疲劳、心理应激等的作用,一般情况下此时赶超难度较大,意味着此阶段能少动用些机能储备,使泳速适当下调对比赛名次影响不大。更重要的是,这能使更多的机能储备被预先应用至途中前段泳度的提升中,使机体能量的利用更加经济,更有助于获得较好运动成绩。
另外,该项目中泳速在途中前段较高,在结束阶段较低,可能是一种较好预期反馈调节能力的体现。
运动节奏是运动员主观调节的结果[16],其调节能力影响着良好运动节奏的实现与否。以往在 1 500 m 自由1或者运动员自身耐力素质差所致[6,10],这样认为是不全面的,这有可能是由于为了实现良好的运动节奏运动员有意识或无意识主观调节所引起的。预期反馈调节是 Tuck[17]于 2009 年提出一种运动节奏调节理论,认为通过对运动前生理状态、比赛距离以及持续时间、运动经验和动机水平等预期,对赛中生理状态、运动状态以及运动阶段等信息的反馈,从而实施对运动节奏的调节。当具备较高预期反馈能力时,能够充分把握现实状态与预期运动状态间的差异,能够在途中前段充分的发挥速度,较少受到为随后阶段( 特别是结束阶段) 预留速度储备用于冲刺这种顾虑的影响,使机能得到合理分配。当此能力较弱时,将会对现实与预期运动状态差距估计不足,往往受到上述顾虑的影响后,在途中前段抑制速度发挥,在结束阶段竭力释放能量,提高泳速,从而造成机能利用效率较低。
划频与划幅则是泳速的两大决定因素,也体现了优秀运动员的专项技术特点,是专项运动技术训练中重要监控指标[3 -4]。从本研究结果中可见,这 2 个参数与运动成绩间也存在高度相关关系。它们有可能通过影响泳速、运动经济性以及体现 1 种积极的主观态势对运动成绩发生作用,导致这种高度关联关系的产生。此外,研究结果中进一步显示,运动成绩较好时,途中前期划频较高、划距较低; 在结束阶段划频较低、划距较高( 图 2B2、C2) 。1 500 m 自由泳中划频在开始阶段持续下降,基本上到途中前期达到最低值,并且在途中阶段保持稳定状态,随后在结束阶段中急剧提高至最大值; 划距的变化则相反。可见,运动成绩较好时在途中前期划频降幅小,展现出运动员积极争取心理与战术优势; 在结束阶段中划距增幅较大,这是运动员在机能大量消耗后奋力维持速度的举措。
这些都体现了优秀运动员积极的主观态势。由于划频与划幅受运动时间不同影响而相互抑制,致使这两者间存在高度负相关关系,划频的提升会导致划距一定程度下降,同理,划幅的增加会导致划频一定程度的降低。另外,与泳速变化特征一样,较好运动成绩时运动全过程中划频与划幅变化幅度较小( 图 2 B2、C2 中反映更直观) ,可见,在 1 500 m 自由泳项目中避免游进状态大范围起伏尤为关键。
函数型主成分分析方法是 1 种体育运动中阶段速度等时间序列性参数特征探索的重要工具,具有独特的功能。本研究细致的考察了函数性主成分方法在此方面的适用性,包括应用条件、参数设置、统计量诠释、特有功能等方面分析,并且在 1 500 m 自由泳项目中得到了较好的应用,认为其是一种能应用于速度节奏或速度分配量化诊断、优化、监控的好方法。采用函数型主成分方法量化这些时间序列性参数的优点主要有两大方面: 1) 在以往各运动等级间、不同运动成绩或名次间阶段速度等直接比较中往往不能剔除各阶段速度间相互关联对比较结果的影响,采用函数型主成分方法以整个阶段速度曲线为单位加以分析能够充分考量此因素的作用; 2) 由于比赛中的阶段速度形成受到多种因素的综合影响,其会表现出一定的多样性,如果将不同类型阶段速度曲线不加以分离直接进行比较分析,有可能影响结果的可靠性以及丰富性,采用函数型主成分方法在此方面具有独特优势。
4 结 论
函数型主成分方法适用于体育运动中阶段速度等时间序列性参数特征的探索,通过该方法的优点是充分考虑到了各阶段速度间相互关联及其不同曲线类型对速度节奏诊断与优化结果的影响,是 1 种能应用于速度节奏或速度分配量化诊断、优化、监控的好技术。基于该方法的分析认为,优秀 1 500 m 自由泳运动员阶段速度、划频以及划距曲线”途中前段-结束“阶段间非线性互补波动形式与运动成绩间关系密切,运动成绩较好时,泳速和划频在途中前段倾向于较高,在结束阶段较低; 划距在途中前段倾向于较低,在结束阶段较高。这些被认为是良好竞赛策略、体能分配模式、预期反馈调节能力等的表现。
参考文献:
[1]靳刘蕊 . 函数性主成份分析的思想,方法及应用[J].统计与决策,2010( 1) : 15 -18.
[2]孟银凤,梁吉业,原曦曦 . 函数性数据分析中的主成分分析[J]. 山西大学学报: 自然科学版,2011,34( 1) :21 - 25.
[3]温宇红,林洪,程燕,等. 我国重大游泳比赛技术参数采集与分析系统的应用研究[J]. 武汉体育学院学报,2005,39( 12) : 65 - 68.
[4]周晓东,程燕,林洪 . 游泳比赛技术监测系统的研究[J]. 中国体育科技,2008,44( 4) : 84 -86.





