3.4 SMP模型分析
通过对系统工作流程以及FSM的分析可见,系统的状态转换过程满足以下三个特点:
1.系统的状态转换过程具有马尔科夫特性,即系统即将转换的状态只与系统当前的状态有关,而与历史状态无关;
2.状态的转换是入侵行为、入侵检测以及入侵容忍在时间域上的一个积累过程;
3.系统状态转换遵循马尔科夫链,但在每个状态的停留时间是随机分布的,即状态变化的时间间隔是随机变量。
半马尔科夫过程(SMP:Semi-MarkovProcess)可以看作是马尔科夫链的推广,它不再局限于马尔科夫链中的假设,而假设当前状态的变化不仅与当前所处状态相关,也与在当前状态逗留的时间相关。概率分布,性的能力。而非具有无记忆性的指数分布。
状态保持时间的分布可以是任意可能的这使得半马尔科夫过程具备描述长相关我们建立自适应动态取证系统的半马尔科夫模型,将对整个系统的研究转化为对不同状态的研究及对各状态之间转换性质的研究。半马尔科夫模型与马尔科夫模型的主要不同就在于:
1.系统状态之间的转移概率不是常数,而与状态停留时间有关;
2.在各个状态的停留时间分布不是指数分布,而可以是任意概率分布。
入侵的代价是分析模型安全性能的一个关键因素,代价可以用入侵者花费的时间、金钱以及精力来表示,为便于分析,我们可以用时间代价来表示入侵代价。因此,我们可以考虑入侵以及响应过程中不同状态之间的转移变迁和驻留时间,通过半马尔科夫过程过程中安全状态和不安全状态的稳态概率来对该模型进行安全性能的量化分析。
截图1

截图2

3.4.1 SMP模型
为了对系统的SMP模型进行分析,我们将3.3节的状态转移模型抽象后得到其嵌入离散马尔科夫链(DTMC,如图3-9所示。
图3-9
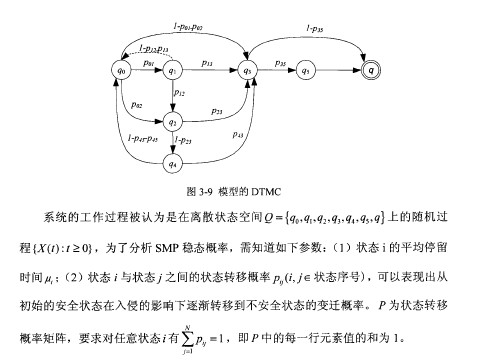
截图3

截图3.下

截图4

返回本篇论文目录查看全文 上一章:框架的FSM模型 下一章:入侵实例分析





