摘 要: 通过对晋南地区三所高职学院学生心理健康咨询中心150份病例资料的相关典型症状进行属性提取,转化为疾病知识库,利用基于粗糙集的决策表属性约简算法,构建可识别矩阵,生成最小值简化信息表,最后总结出约简规则,与学生临床表现之间形成了相关的逻辑关系,并结合学院心理咨询师的临床实践,形成了一个完备高效的心理疾病诊断知识库,为高校大学生心理问题的诊断提供了一个行之有效的方案。
关键词: 粗糙集; 大学生; 心理问题; 诊断;
Abstract: Attribute extraction was conducted on the related typical symptoms of 150 case data of student mental health counseling centers of three vocational colleges in south shanxi,into a disease knowledge base, the attribute reduction algorithm of decision table based on rough set is used,construct the recognizable matrix,generate minima to simplify the information table,summarize reduction rules,with students formed the relevant logic relationship between clinical manifestation,and combined with the clinical practice of college psychological consultants,formed a complete and efficient mental disease diagnosis knowledge base,it provides an effective scheme for the diagnosis of college students' psychological problems.
Keyword: rough set; college students; psychological problems; diagnose;
随着高校自2003年来的连年扩招,在校大学生总人数呈快速上升趋势。大学学习阶段是每名学生的世界观、人生观和价值观形成的重要时期,心理因素在其中起着非常重要的作用,健康的心理是一位优秀人才必须具备的先决条件之一。但是在我国,有数据显示自20世纪80年代中期,高校学生中心理障碍的人数所占比例约为23%~25%,到90年代这一数字上升至25%,进入21世纪以来更是高达30%以上,各高校发生的残害同学、跳楼自杀等现象屡见不鲜。2009年中国疾病预防控制中心的一项调查显示,全国大学生中,有高达25.4%的人有焦虑不安、神经衰弱、强迫症状和抑郁情绪等心理障碍。中国心理卫生协会大学生心理咨询专业委员会的调查表明,40%的大学新生和50%以上的毕业生都存在或多或少的心理问题。
虽然目前教育部要求各高校必须建立学生心理咨询中心,配备心理咨询师,积极进行学生心理辅导工作。但短时间内一是因心理辅导师紧缺,好多高校没有足够并专业的心理辅导师;二是因心理辅导师质量参差不齐,虽然有的高校有一定数量的心理辅导师,并具备人社厅颁发的心理辅导师证,但因辅导时长有限、专业知识有限、经手案例有限等种种原因,导致辅导师不能很好地为学生服务。因此,如何准确、高效的判断学生心理疾病,及时做到心理干预是关键,解决这一问题的途径之一,就是建立一个快速、有效而又相对完备的心理问题分析决策知识库。
文章所研究的方向就是利用粗糙集属性约简算法,以大学生心理问题知识库为对象,对收集到的心理问题资料数据库中的数据进行约简分析,从中整理出心理问题的相关分类知识,用来建立决策规则,辅助心理咨询教师进行大学生心理问题的诊断。
1、 粗糙集相关知识
1.1 、粗糙集理论介绍
粗糙集理论是数据分析和处理理论中的一种,在1982年由波兰科学家Z.Pawlak最先提出[1],并于1991年出版了一本有关粗糙集的专门论着[2],主要内容是收集到数据后直接进行分析和推理,从数据中揭示潜在的规律并剔除那些对结果影响并不重要的部分,用来处理那些不精确(imprecise)、不一致(inconsistent)和不完整(incomplete)的数据[3,4],主要优点有两点:一是数学基础成熟、不需要提供除问题所必须处理的数据集合之外的任何先验知识;二是易用性,能够得出问题属性的最需要部分,找出解决问题的最小属性集,去除数据中的不需要信息。用到的数据挖掘方法主要是基于概率论的数据挖掘、基于模糊理论的数据挖掘和基于证据理论的数据挖掘[5,6]。

1.2、 粗糙集理论解释
假设U为包含若干对象的非空有限集合,在集合中,另外的任意集合R?U为一个指定的范畴。而由任意个集合R组成的子集群体形成了U这个对象中的所有内容,简称为知识。在给定的集合中,任意选择一个等价关系集R,我们可以得到一个二元组S=(U,R),称这样的二元组视为一个知识库(近似空间)。一个信息系统S可以表示为一个四元组S=(U,R,V,f)。其中,U为包含若干对象的非空有限集合;R为属性集合,R=C∪D,C是条件属性,D是决策属性;V为属性值域,f为从U×R到V的信息函数。[7,8]
粗糙集中的属性是知识集中表述内容的最小单元,基于粒度的知识的变化其本质上是属性值的改变,知识集中的各个属性对知识本身的影响是不一致的,也就是说属性的重要性是不一样的。从数学角度上看,不同属性的重要与否其表现为剔除该属性后知识集正向区域的改变有多大,粗糙集运算的时间复杂度也要取决于区域的大小。所以,对该属性的计算其本质上就是对属性重要性的求解,求得的值如果大于0,该属性就是知识集的核属性,对该属性计算的复杂度就是S(|C|R||U|lg|U|),其中C是条件属性,R是属性集,U是非空有限集合。
用来对知识进行展现的系统一般以二维表的形式来表达,二维表内要进行研究的对象是它的属性集合R,R由条件属性C和决策属性D组成,组成的表被命名为决策表,通过决策表可以发现知识的决策属性和条件属性的关系,从而使用更少的条件得到决策要求,被称为属性约简,又可以通俗的称为“知识的简化”,属性约简有一必要条件,那就是一定要保证对知识进行分类的能力不变的前提下,尽可能的减掉对分类无关的属性。决策表的简化有两点,分别是属性的约简(求核属性集)、属性值的简化(决策规则集。)
属性约简可由可识别矩阵进行计算,可识别重矩阵是由波兰的着名数学家skowron提出来的,它的数学模型定义为:系统S=(U,A),U={u1,u2,…,un},a(u)是u在属性a上的值,D(u)是u在属性D上的值,则可识别矩阵用数学模型表达为:
该矩阵的对角线元素值都是0,并且该矩阵是对待矩阵,所以实际上用下三角矩阵也可以表示。从上述数学表达的矩阵可以看出,矩阵内容中属性组合数是1的内容中只有该属性可以区分,其他的属性没办法把决策不一样的另外两条记录分别开来,由此可知此属性应该留下来,该属性和粗糙集决策表内的核属性地位是相同的。
2、 对决策表进行约简
在现有知识集合中,一个很重要的问题就是对其进行属性的约简和属性值的简化,也就是求其核属性集和决策规则集。运用粗糙集解题的相关方法求解知识集合中决策表的核属性集和决策规则集,可以得出核值表(也称为最小简化表),常用方法分两步走:第一步,扫描决策表中的全部属性,对属性进行约简;第二步,再次扫描决策表中的全部属性值,对值进行约简。该方法的优点是扫描全面,缺点是当数据量大时,扫描费时费力。事实上在现实应用中,为了达到相对高的切合率,所涉及的数据量大部分都非常大。文章因此采用另外一种计算相对简便的算法,就是采用可识别矩阵求核来对属性进行约简,具体过程为:首先,进行一次决策表扫描,在矩阵中求组合数结果为1的属性集,得到的属性即为核属性,构建一张仅含有核属性的决策表;其次,第二次扫描时仅扫描含有核属性的决策表,然后对属性值进行简化;最后,得到了含有核属性和简化后属性值的简表[9,10,11]。
运算过程为:
step1:定义知识集合的条件属性C和决策属性D,剔除其中的重复内容,构建基于本知识的决策表;
Step2:根据决策表,构建其可识别矩阵;
Step3:通过矩阵运算,找出属性组合数是1的内容属性集,得到核属性;
Step4:去除非核属性,形成该决策表的决策规则表;
Step5:二次扫描,对核属性的属性值进行约简;
Step6:形成结果,结束。
3 、大学生典型心理问题表现症状数据分析
3.1、 实验数据及处理
笔者由山西省晋南地区三所高职院校学生心理健康咨询中心各获得50份学生心理问题病例资料,共获得150份,根据典型表现建立了没有重复例子的知识表达系统(具体内容见表1),表内共包含15种属性,前14种属性为典型症状的条件属性C,最后为判断结果的决策属性D,转化为决策表以后可以见表2[12]。
表1 大学生心理问题典型症状知识库
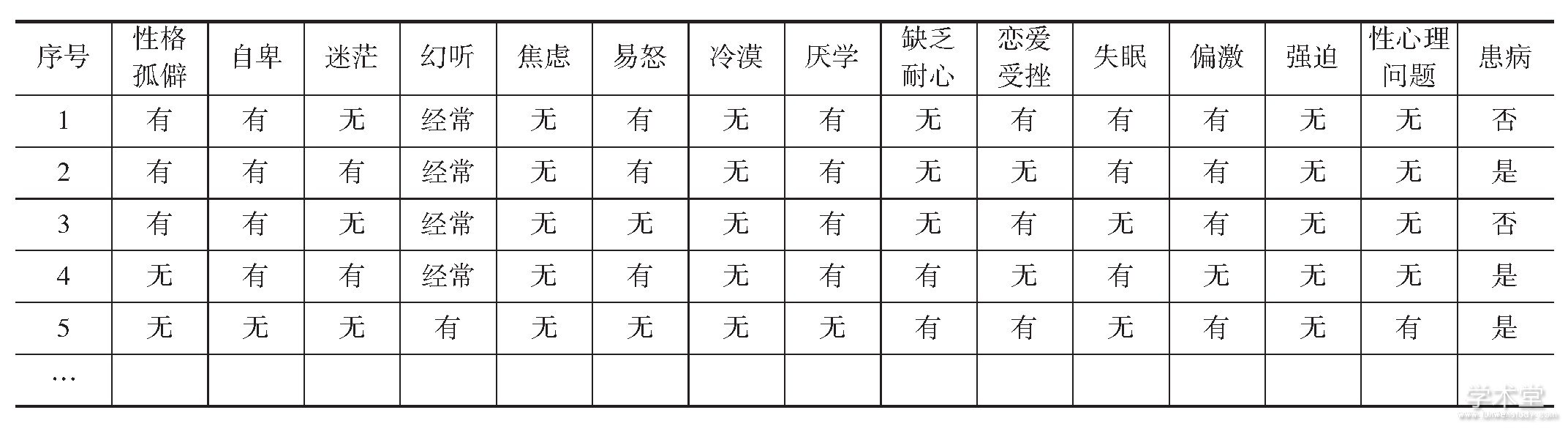
其中:属性如下:a-性格孤僻;b-自卑;c-迷茫;d-幻听;e-焦虑;f-易怒;g-冷漠;h-厌学;i-缺乏耐心;j-恋爱受挫;k-失眠;l-偏激;m-强迫;n-性心理问题;o-患病;
条件属性记录值:1-有;2-无;3-有时;4-经常;决策属性记录值:1-是;2-否;
表2 基于知识的决策表
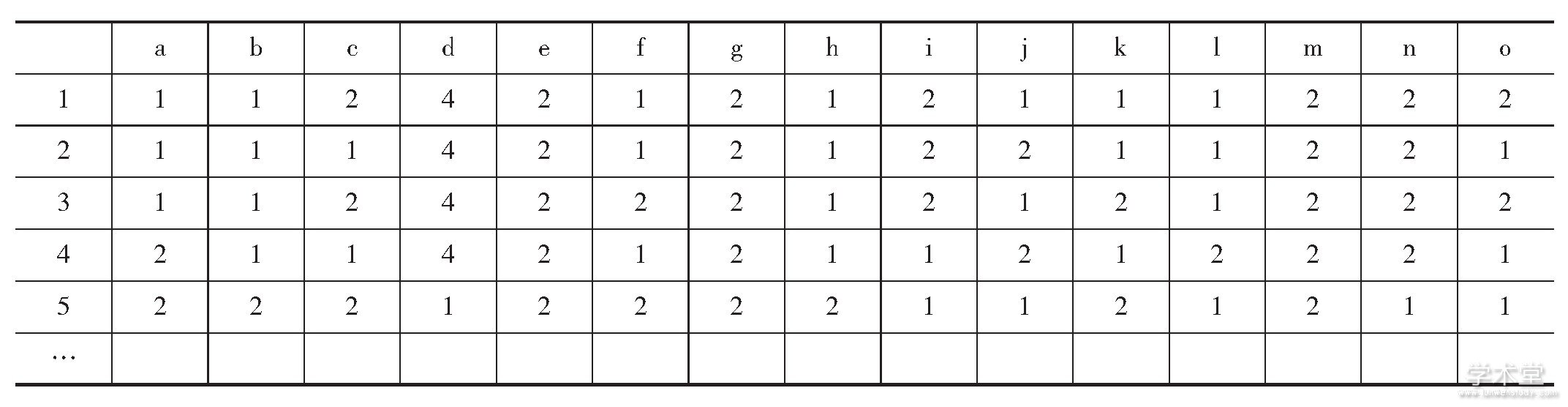
根据决策表,构建其可识别矩阵,见表3:
表3 根据决策表构建的可识别矩阵
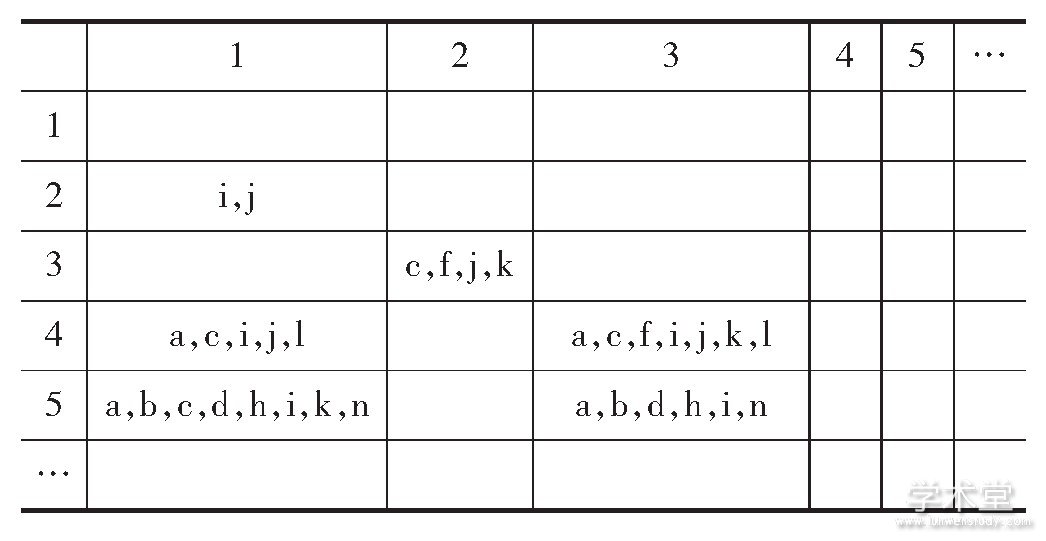
根据决策表构建的可识别矩阵,通过对可识别矩阵进行运算,找出了属性组合数是1的内容属性集,得到了核属性,具体核属性集如下:
对核属性的属性值进行了二次扫描,对核属性的属性值进行约简,得到了表4的内容。
表4 属性值约简后的简化表
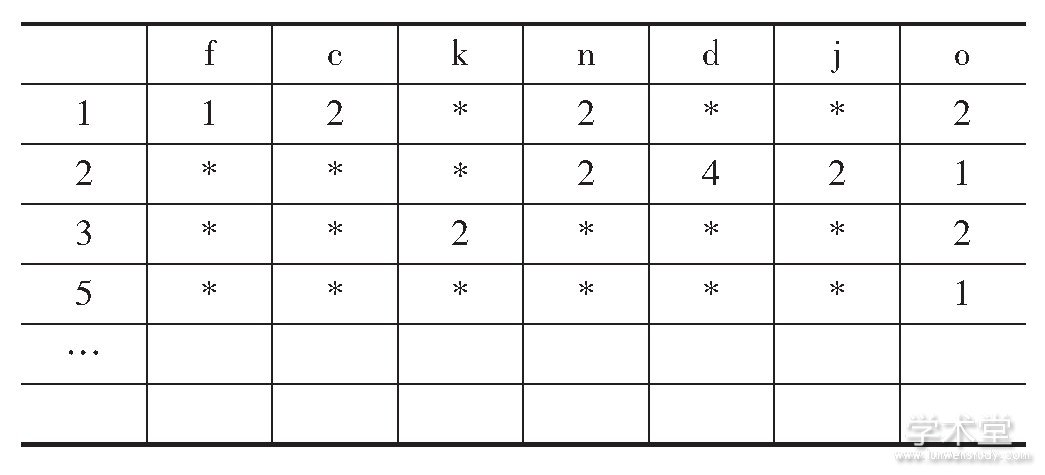
根据约简后的简化表,可将规则总结成以下内容:
(1)患心理疾病的判断依据:一是经常性的幻听,可以判断出患心理疾病,也就是d=4时可得出o=1;二是有易怒情绪、有性心理问题、同时有时会有幻听情况,可以判断出患心理疾病,也就是(f=1)∩(n=1)∩(d=3),可得出o=1。
(2)未患心理疾病的判断依据:一是没有失眠症状不患病,也就是k=2时可得出o=2;二是没有出现幻听情况,同时也没有出现恋爱受挫情况,则不患病,也就是(d=2)∩(j=2)可得出o=2;三是没有出现易怒情况,即使有性心理问题同时有时会有幻听情况也不患病,也就是(f=2)∩(n=1)∩(d=3),可得出o=2。
3.2、 对实验结果进行提取并分析
根据上面的知识原理和运行过程,形成大学生心理问题典型症状知识库,调入计算机中,配置TC2.0运行环境,进行编译后输出基于知识内容的决策表、根据决策表构建的可识别矩阵,并算出各属性位置相对的组合数、核属性集、核属性集组成的决策规则表和属性值约简后的简化表,将本来的14种典型心理问题表现减化为6个,即:迷茫、幻听、易怒、恋爱受挫、失眠和性心理问题,属性约简率为57.14%,属性值约简率为61.82%,根据生成的结果与三所院校最近产生的心理问题和心理疾病判断结果进行比对,发现对心理问题的诊断正确的概率为66.84%。随后,研究人员对研究样例进行了扩大,对150份的全部相关内容进行了知识库的编排,经过运算后得出核属性集为10个,属性约简率为28.57%,属性值约简率为36.65%,对心理问题诊断正确的概率上升为86.84%。由此可以看出,只要样本有一定的数量和典型性,对样本处理的结果准确,那么得到的结果判断规则可信度还是非常高的。另外,利用粗糙集进行约简的另一个优点是,在处理大批量的数据时,本算法具有非常大的优势。如果知识集较少,那么得到的结果准确率也将下降,处理优势也不明显。
4 、结束语
根据粗糙集的数学特征,利用粗糙集属性约简算法来对大学生心理问题典型症状知识进行处理,不需要相关的心理学疾病知识和诊断经验技能[13],对于目前学生心理问题频发,高校在心理咨询方面的薄弱等相关问题有很强的针对性,对处于工作岗位上的心理咨询师们进行诊断是一个很好的参考和补充。接下来,如何更好地提升对心理问题的诊断准确率是关键,同时由于社会环境的出现和信息技术的广泛使用,学生心理问题的典型表现会发生变化。如何利用大数据技术更多地获取学生典型表现并用来提升诊断的准确率是进一步研究的方向。
参考文献
[1]文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社, 2001.
[2]赵青杉,王建国,刘婧.基于粗糙集的风湿性二尖瓣狭窄疾病诊断[J].太原科技大学学报,2006,27(3):177-180.
[3] Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences,1982;(11):341~356.
[4] Pawlak Z.Roughsets.Theoretical Aspects of Reasoning about Data[M].Dordrecht:Kluwer Academic Publishers,1991.
[5]邬阳阳,汤建国.大数据背景下粗糙集属性约简研究进展[J].计算机工程与应用,2019,55(6):31-38.
[6]胡建强,王元.基于粗糙集的慢性病变分级方法[J].计算机系统应用,2018,27(12):268-273.
[7]李华,江峰,于旭,等.基于粒度决策熵的属性约简[J].计算机与现代化,2018,272(4):7-12.
[8] Jiang Feng,Sui Yuefei,Zhou Lin.A relative decision entropy-based feature selection approach[J].Pattern Recognition,2015,48(7):2151-2163.
[9]张伟,徐章艳,王晓宇.一种结合概率启发信息和知识粒度的属性约简算法[J].计算机应用与软件,2013,30(7):43-45.
[10]鄂旭,高学东,焦吉成,等.基于粗糙集的客户市场细分算法[J].清华大学学报,2006,46(S1):1064-1068.
[11] Hu X H, Cercone N. Learning in rel ational databases:A rough s et approach[J]. Com putational Intellig ence, 1995, 11(2):323-337.
[12]王江荣,白保琦.基于粗糙集的Probit回归模型在煤炭种类识别中的应用[J].工业仪表与自动化装置,2018,27(04):12-15,131.
[13] 邓志轩,郑忠龙,邓大勇. F-邻域粗糙集及其约简[J].自动化学报,2019,46(3):1-11.





