
1、 引言
仓储是物流系统中一个非常重要的环节,仓库的数目、空间分布及仓库利用率等,都是直接影响企业成本效益的重要因素。尤其是连锁经营的超市,由于超市经营的物品种类繁多,所以为连锁超市供货的供应商数目比较多,涉及到的物品种类繁多,数量较大,仓储管理活动比较复杂。目前为连锁超市供货的供应商大都是自建仓库或租用别人的仓库,由于供应商各自为政,缺乏对仓库的合理规划,自建或租用的仓库大部分利用率都很低。对各个仓库进行管理均会产生一定的仓储管理成本,这无形中增加了各个供应商的仓储成本。所以,为增加企业效益、满足客户需求,有必要对不同供应商的仓储物流活动进行协同管理。
本文拟以A城市B连锁超市的供应商为研究对象,在综合考虑各供应商的仓库储存物品种类的相似性及各个仓库仓储容量的前提下,对各供应商的仓库进行聚类,进一步提出共享仓储资源的仓库混同策略,实现降低供应商的仓储成本、增加各供应商效益的目标。
2、 B连锁超市供应商仓库布局现状及存在的问题
2.1 B连锁超市供应商仓库布局现状
A城市B连锁超市的规模比较大,共有5家连锁分店,均匀分布于整个城市的不同位置。
连锁超市经营的产品种类多,品牌也很多。目前,为5家连锁超市供货的供应商共有20家,每家供应商同时向多个超市供应多种物品。为满足各超市的产品需求,并对产品需求做出及时响应,20家供应商对每类供应的产品都储备了一定的库存,其中17家供应商的库存货物存放在自建仓库中,另外3家供应商的库存货物存放在租用仓库中。这20个仓库随机分布在A城市的不同位置。
2.2 供应商仓库布局存在的问题
根据市场调研发现,A城市B连锁超市的20家供应商仓库布局方面存在以下几个方面的问题:
(1)资源利用率低。一方面,由于日用产品和生鲜食品类产品保质期较短,最大库存量不宜过多,而超市每天的销售量是随机变化的,这极易造成库存积压或仓库利用率低,导致资源浪费。另一方面,有些产品(如生活电器类产品)销售量较小,这会导致产品的库存周转率较低。以上两方面都在无形中造成了仓库资源的浪费,加大了供应商的仓储管理成本。
(2)仓储管理成本高。不同产品的储存需要不同的条件,比如一些生鲜类产品,需要在冷库中储存,其对冷库的温度、湿度、通风等条件要求比较苛刻,食品类产品则需要在干燥通风的地方储存,需要对仓库及时通风。为保证产品的质量,各供应商必须花巨资创造一个好的产品储存条件。各仓库还必须安排专业的仓库管理人员去管理,仓库管理人员的工资也是供应商一项很大的开支。
考虑到以上两方面的问题,如果能够将供应物品相似的多个供应商的仓库合并在一起,共同为连锁超市配送货物,则可以有效降低各类物品的需求随机性,减少总库存量、降低库存管理成本。
3、 供应商仓库地点混同问题的数学模型及求解方法
3.1 仓库地点混同的定义
将位于不同区域或地点的仓库中的库存物品合并存放到一个地点的库存策略称为仓库地点混同策略(Warehouse Lo-cation Pooling Strategy)[3]。由于不同物品的储存条件不同,只有把储存物品相同或相似的仓库合并才能有效降低仓储成本,因此可以先根据各个供应商仓库中储存物品种类的相似性对仓库进行聚类,然后再分别将每一类供应商的仓库合并成一个仓库。
3.2 供应商仓库混同问题的数学模型
本文首先根据各个供应商仓库中储存的物品种类计算供应商仓库的相似度指标,然后在考虑混同后仓库容量限制的前提下,建立供应商仓库混同问题的数学模型。假设A城市共有n个供应商为B连锁超市供应m类不同的物品,已知各个供应商仓库中储存的物品种类,现欲将n个供应商的仓库合并成k个混同仓库,每个混同仓库中最多能容纳C个供应商仓库的物品。
首先把各个仓库中储存的物品种类表示成一个m维向量:

利用两个仓库储存物品的种类向量 Bi、Bj,计算两个仓库之间的相似度 rij,并用表格表示。其中相似度 rij的计算公式为:
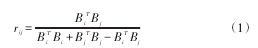
然后根据仓库之间的相似度,建立仓库混同问题的数学模型。设:

目标函数(2)表示极大化混同在一起的各组仓库平均相似度之和;约束条件(3)表示每个仓库恰好被合并到一个混同仓库中;约束条件(4)表示每个混同仓库最多可以容纳C个仓库的物品;约束条件(5)是变量取值约束。
3.3 算法设计
对于规模较小的整数非线性规划模型,可以直接编程序求解得到问题的精确最优解,对于规模较大的问题,可以采用基于聚类分析的启发式算法求解,启发式算法步骤如下:
第一步:从仓库的相似度表中找出相似度最小的两个仓库i和j,并将相似度最小的两个仓库分配到第一组和第二组,转第二步。
第二步:找出和仓库i,j相似度都较小的一个仓库s,将其分配到第三组,再寻找和仓库i,j,s相似度都较小的仓库t,分配到第四组……,直到找不出和之前各组相似度较小的仓库为止,此时,聚类分组个数已经确定,转第三步。
第三步:任意选择一个未分组仓库,计算该仓库与各组中所有仓库的平均相似度,选择平均相似度最大的一组作为该仓库的分组,将该仓库加到相应分组中。重复第三步,直到把所有的仓库都分配到了合适的组,停止。
在上述聚类过程中,当遇到未分组仓库和两组以上仓库的平均相似度同时达到最大时,优先将该仓库分配到包含仓库数量较少的组;当各组包含的仓库数量相同时,则任选一个组。
4、 A城市B连锁超市20个供应商仓库混同问题的求解结果及分析
4.1 20个供应商仓库混同结果
本文考虑为B连锁超市供货的20个供应商仓库的混同问题,这些供应商的仓库随机分布在A城市的各个地方,将20个仓库编码为1,2,...,20。现欲将20个供应商的仓库合并成5个混同仓库,每个混同仓库最多容纳5个供应商仓库的物品。20个仓库中共储存了61个品牌的6类物品,将每一个仓库中储存的物品种类表示成一个6维0,1向量,见表1(其中每一列对应一个仓库中的物品向量)。
根据式(1)计算20个仓库之间的相似度,结果见表2。如果相似系数0≤r≤0.6,则定义物品种类相似系数较小;如果相似系数0.6<r≤1,则认为物品种类相似系数大。
根据表2,利用Lingo软件编程直接求解模型,可以得到20个仓库混同为5组的结果为:第一组:仓库1,4,10,19,20;第二组:仓库2,9,12,13;第三组:仓库3,7,11;第四组:仓库5,6,14,17;第五组:仓库8,15,16,18。目标函数值为4.497 85,即混同后各组仓库的平均相似度之和为4.497 85。
利用启发式算法对该问题进行求解的步骤如下:
第一步:从仓库的相似度表中找出相似度最小的两个仓库1和2,并将其分配到第一组和第二组。
第二步:找出和仓库1,2相似度都较小的一个仓库3,将其分配到第三组,再寻找和仓库1,2,3相似度都较小的仓库5,分配到第四组,再寻找和仓库1,2,3,5相似度都较小的仓库8,分配到第五组,至此找不出和仓库1,2,3,5,8相似度都较小的仓库,聚类分组个数已经确定,共分为5组。
第三步:任意选择一个未分组仓库,分别计算其与各组仓库的平均相似度,并将其分配到平均相似度较大的组。本例中,先取未分组仓库4,由于仓库4与第一组中的仓库的平均相似度最大(平均相似度为1),因此将4分配到第一组;然后选取未分组仓库6,由于仓库6与第四组仓库的平均相似度最大(平均相似度为1),因此将仓库6分配到第四组,重复以上步骤,直到把所有的未分组仓库都分配到了合适的组为止。
经过计算发现,利用启发式算法得到的分组结果与精确算法得到的分组结果完全相同。
4.2 仓库地点混同前后的成本比较
通过仓库的地点混同可以降低供应商的仓库管理成本,但不会降低服务水平。由于每个供应商的规模相差不大,在仓库建设及管理方面的投资大致相同。为便于分析,假设在仓库地点混同之前和混同之后,建立每个仓库的固定资产投资成本相同,均为20万元,每年各个仓库的管理费用为3万元。
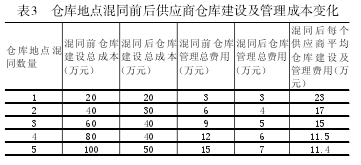
仓库地点混同前后供应商的平均仓库建设及管理成本变化见表3。
根据表3并结合前面的计算结果得出,20个供应商的仓库地点混同之前总的仓库建设及管理成本为115万元,而仓库地点混同之后,20个供应商总的仓库建设及管理成本为57万元,成本降低了50.43%,平均每个供应商的仓库投资成本降低了11.6万元。
分析仓库地点混同前后的方案及总成本可以看出,仓库地点混同后,仓库的数量由原来的20个减少到5个,仓库的总建设成本和管理成本均大大降低了。由于仓库地点混同后,各供应商可以共享仓库资源,所以通过提高仓库的硬件设施可以为更多的超市物品提供更好的储存条件,满足超市产品的质量要求。
5 结论
本文讨论了A城市B连锁超市20个供应商仓库的地点混同问题,结果显示,采取仓库地点混同策略,以大大降低供应商的仓储成本。但本文只是根据仓库储存物品的种类相似度计算仓库之间的相似度,并没有考虑仓库的地理位置对相似度的影响,同时,在对结果进行分析时也只是分析了仓库地点混同前后的仓储成本变化,而没有考虑仓库地点混同前后运输成本的变化。事实上,仓库地点混同后,在减少仓储成本的同时有可能增加运输成本。在解决实际问题的过程中,如果要把运输成本考虑在内,可以先利用仓库之间的距离对相似度系数作一个修正,然后再按照本文的模型及算法进行计算。
参考文献:
[1]丁凯,蒋志明,谈琳.基于聚类分析的电网设施仓库宏观布局规划研究[J].物流科技,2009,(6):29-32.
[2]祝丽,汝宜红,罗平.基于聚类分析电信运营企业仓库布局优化研究[J].物流技术,2007,26(8):106-109.
[3]杰拉德·卡桑,克里斯蒂安·特维施,著,任建标,译. 运营管理[M].北京:中国财政经济出版社,2007.
[4]李诗珍,杜文宏.基于聚类分析的订单分批拣货模型及启发式算法[J].统计与决策,2008,(12):53-56.
[5]汪应洛.系统工程[M].北京:机械工业出版社,2012.





