
0、引言
同时重建混合气体的温度场、各组分浓度分布及流场对于系统监测、改善系统效率、减少污染排放具有重要意义.现有的混合气体的温度测量方法,主要有热电偶法、等离子体法、光纤法、红外测温及微波吸收法等;气体浓度检测方法,主要包括光谱法,质谱法,气相色谱法等.然而,目前多数方法的测量对象都是单一的,没有对空间中混合气体的温度场、浓度场及流场同时重建.声学法以其非侵入、可获得全场信息、可实现在线监测等优点,而被认为是一种发展前景广阔的测量方法,本文采用声学法进行多种物理场同时重建.在混合气体的温度和各组分浓度未知的情况下,通过一个声学参数无法同时得到这两个未知信息,故选取了同混合气体温度、浓度密切相关的两个参数,声速和声吸收进行研究.声速同混合气体温度、浓度的关系为

式中,c为声速,R为普适气体常数,T为气体温度,gmix为混合气体的比热容比,Mmix为混合气体的平均分子质量,其中gmix值和Mmix值与气体的种类和浓度有关.声吸收同温度、浓度的关系则更加复杂.基于Dain和Lueptow提出的DL弛豫吸收理论及朱明等人对该理论的改进,本文讨论声波弛豫吸收同混合气体浓度、温度的关系.选取一氧化碳、氮气和氧气组成的混合气体,分别建立声速和声吸收同混合气体温度及浓度关系的三维模型,结合声学CT(computedtomography)理论,对混合气体的多物理场进行重建,同时对误差原因及最佳声波频段进行讨论.数值实验表明该算法可用于混合气体的温度、浓度与流动的同时重建.
1声吸收与温度、浓度关系的推导
1.1声波吸收计算的简化
声波在气体中传播,若无散射存在,造成声波衰减的主要原因有两种:声波扩散引起的能量密度减小,即声波传播中因波阵面扩大而导致的声能量密度的减弱;声波能量在传播过程中被介质吸收引起的衰减.声衰减的计算式为
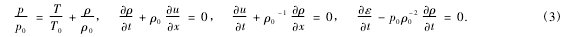
式中的I是接收点的声强,I0是初始声强,Id为波阵面扩散引起的声强衰减,Ia为介质吸收引起的衰减.其中,扩散衰减与声源的形状有关,与介质的性质无关,由于本文发射的声波为球面波,所以声波的扩散衰减占较大的比重,要将该部分衰减加以考虑,具体计算过程参见文献.气体中的声吸收由经典吸收和弛豫吸收加性组成.由于经典吸收主要作用于高频声波,在低频和中频段,其影响可忽略不计,故本文忽略经典吸收,用弛豫声吸收直接代替声波的吸收.如图1,以一氧化碳、氮气和氧气组成的混合气体为例,其中O2和N2固定浓度比为21:78,本文首先计算了不同声波频率下声波的经典吸收和弛豫吸收.图1中实线从左到右分别表示CO浓度为10%、50%和90%时候的弛豫声吸收,虚线则代表三种浓度下声波的经典吸收.从图中可以看到,若选取的声波频率为中频或低频,弛豫声吸收远大于经典声吸收,经典吸收可忽略不计,为本文简化的合理性提供了支持依据.
1.2简化的DL弛豫吸收模型根据气体分子碰撞能量转移理论,计算气体分子的弛豫吸收时,应将分子的所有振动模式都加入碰撞能量转移模型.本文选取的气体组合为一氧化碳、氮气和氧气,这三种气体都只有一个振动模式,在一定程度上简化了DL计算模型.DL模型基于欧拉气体方程,包含了混合气体分子振动模式的内部温度的声学方程可表示为

当气体处于声波“压缩/舒张”的过程时,式(3)中的p、r、u、ε和T表示压力、密度、速度、分子能量和温度在平均值附近小幅度的波动.
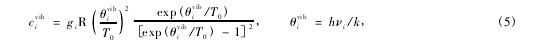
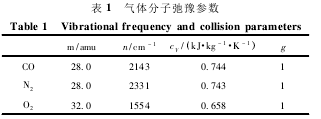
式中,νi为振动频率,θvibi为振动特征温度,gi是与振动频率有关的退化方式.h=6.626×10-34J·s为普朗克常量,k=1.38×10-23J·K-1为波尔兹曼常数.表1中列出了关于这三种气体的一些物理量.式(4)中的振动温度则由微分方程(6)得到
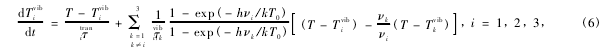
式中,τtrani为平动弛豫时间,τvibi,k为振动弛豫时间.二者的详细计算见文献.表2中列出了在常温下(298K),本文计算的50%CO的混合气体的弛豫时间.将式(5)、(6)带入式(4),与方程组(3)组成一个微分方程组,方程组的未知变量为p、r、u、T和Tvibi,由于这些值都代表了在平均值附近的波动,将其写成如下的形式由于B是一个7×7矩阵,方程未知数也为7个,齐次线性方程组有解的条件是B的行列式为0,可由此计算出k值.k通常为一个复数,其虚部就是声波的弛豫吸收系数a.由此,可以得到混合气体温度及各组分浓度同声波弛豫吸收的关系.
2、空间混合气体多物理场重建
2.1模型及算法
根据上述的推导,可以建立两个关系模型:声速依赖混合气体温度、浓度的三维模型,声吸收依赖混合气体温度、浓度的三维模型.基于这两个模型,本文提出的同时计算温度和浓度的算法如下:
如图2(a),若测得声波在混合气体中的传播速度为c0,那么在图中可以做一水平切面,与模型交于一条线.同理,通过得到的声吸收a0也可作一条交线,如图2(b).再将这两条交线投影在温度-浓度坐标系上,两者的交点即混合气体对应的温度和浓度,如图2(c).


在建立声吸收同温度、浓度三维模型时,选取合适的声波频率非常关键.如图1,弛豫吸收曲线的波峰对应的声波频率称为有效弛豫频率,在有效弛豫频率两侧,声波弛豫吸收随频率呈相反的变化趋势.若声波频率选在有效弛豫频率附近,弛豫声吸收依赖气体浓度的曲面变为拱形,等值切线不再单调,无法和声速投影曲线交于一点.所以在选取声波频率建立模型的时候,既要远离经典吸收主要作用的频段,又要避开有效弛豫频率附近的波段,结合本文的实例,选取10kHz作为声波频率.
2.2二维空间声速及声吸收的计算
本文将空间区域划分为20×20个像素,将每个像素内的温度和浓度近似为恒定,利用本文提出的算法,由声速和声吸收可计算出各个像素下的温度和浓度.剩下的一个关键问题是如何获得被测区域内每一点处的声速和声吸收.由于声波在穿过混合气体时,其传播特性的改变是空间不同处混合气体整体影响的效果,根据声学CT方法,可以利用声波的传播时间(timeofflight,TOF)和声强衰减(attenuationofsoundintensity,ASI)以重建出被测区域每处的声速和声吸收,值得注意的是,传感器测到的声强衰减包含了扩散衰减,所以,在此过程中要减去由于波阵面扩散引起的衰减.如图3,在被测区域的四周均匀地布置上声波传感器,用来采集每条声波的传播时间和声强.假设声速为c(x,y),介质自身的流动速度为u(x,y),那么声波在传感器A和B之间的传播时间可表示为
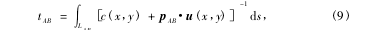
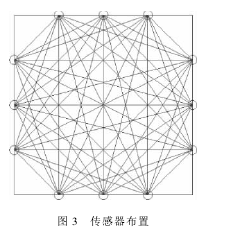

通过式(11),可以得到c(x,y)的重建,再将其代入式(12),实现u(x,y)的重建.在声吸收计算方面,式(2)表达了在扩散衰减Id存在的情况下,接收端的声强,对式(2)进行变换得到介质吸收引起的衰减:
Ia=I0-Id-I,(13)式中的扩散衰减Id可以预先计算,收发端的声强I0和I为测量参数.此时,由式I0-Ia=I0exp(-αx)可以计算声吸收系数α,
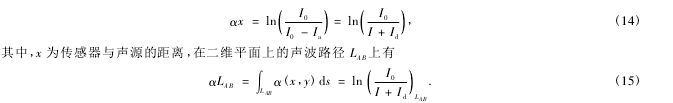
同速度的求法一样,利用反演方法可以获得每点的声吸收系数.在测量数据较少的条件下,本文用高斯基函数组合分别去逼近声速分布、声吸收分布和介质速度分布.高斯基函数的形式为

为了达到较高精度,本文选择30个基函数.三个物理场的q取值分别为:-0.02、-0.62和-0.02.
3、数值仿真及误差分析
3.1数值仿真
仿真模型为一个边长1m的正方形容器,从底部中心处通入具有一定温度的高浓度CO气体,与容器中的N2-O2进行混合,如图4、5.温度变化范围:299K~350K;流场为一漩涡流动,最高流速为4.38m·s-1;容器中一氧化碳浓度范围:20%~99%,由中心向四周扩散.原始的温度场、速度场和浓度场的二维分布由下列公式给定.

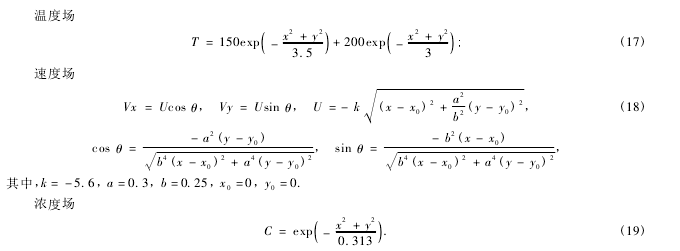
数值仿真分为正问题和反问题两个方向,正问题计算声波经过该区域的TOF和ASI;反问题为由TOF和ASI数据,结合声波的扩散衰减,计算声波在每一个像素下的速度和声吸收,再利用本文提出的算法,重建各个像素的温度和浓度.同时,利用同一路径、不同方向的TOF数据,重建混合气体的流动信息.考虑到实际测量的误差,本文中给TOF数据和ASI数据加上了5%的观测误差,仿真实验在i3-2120CPU,4G内存的计算机的MATLAB软件上进行.图6和图7为重建得到的声速和声吸收在二维区域的分布,从图6可看到,声速的分布形状与温度场分
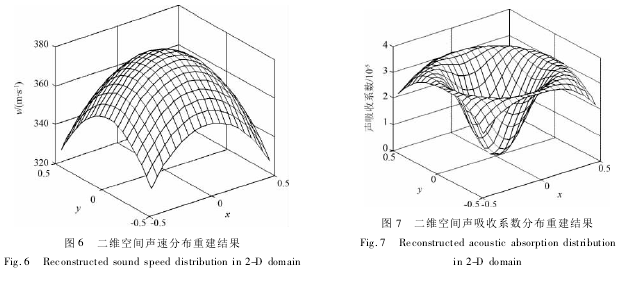
布趋势非常相似,这是因为本文中的气体均为双原子气体,三种气体的比热容比相同,相对分子质量差距也比较小,所以CO-N2-O2组合中,温度变化主导着声速的变化.然而,图7中混合气体对声波的吸收在二维区域中的分布趋势则更加复杂,这也表明了混合气体的温度和浓度共同影响着声波的弛豫吸收.图8和图9为重建得到的流场、浓度场和温度场,重建相对误差见表3.
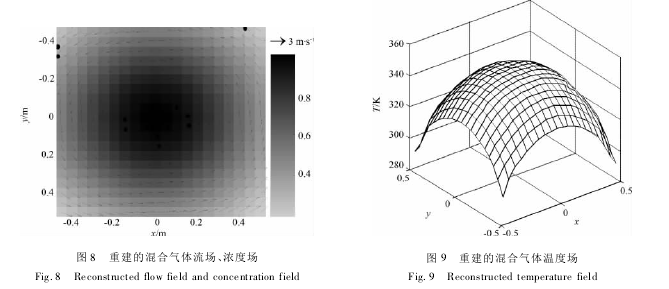

3.2误差分析
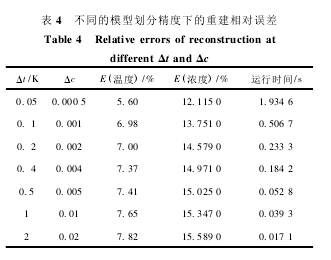
应用本文所提出的算法进行多物理场重建,产生的误差主要包括四部分:测量TOF及ASI时的误差,主要取决于测量的电子仪器的精度及声波中的噪音影响,可以通过多次测量取平均值来减小此部分误差;在计算声速和声吸收的过程中会产生一定的误差,为了更精确的重构本文中的物理场,三个物理场的基函数数量均选为30个,本文的12个传感器会产生54条声波路径,组成的线性方程组属于不适定问题,本文采用了Tikhonov正则化方法解决此问题;由于应用于混合气体浓度检测的DL弛豫声吸收模型是近几年才被提出的,能够进行验证的实验数据较少,弛豫吸收理论还有待于完善.在计算扩散衰减过程中也会产生一定的误差,由于扩散衰减与被测气体性质及声波频率无关,所以在实际测量中,可以通过变换介质及声波频率多次测量,获取准确的扩散衰减.如图2(a)和2(b),在建立三维模型时,不可能将温度和浓度无限地分割.理论上,将浓度和温度划分的越细,重建所能达到的精度就越高,但太多的网格也会影响算法的运行时间,应该从精度和耗时两个方面考虑.表4列出了不同的网格划分精度下,重建物理场的误差和重建耗时.在TOF和ASI数据误差一定的情况下(相对误差5%),本文采取的是Δt=0.1K,Δc=0.001,如果继续加细,重建精度并未明显提高,运行时间却显著增加.
4、结论
在计算声波衰减的过程中,忽略经典吸收,用扩散衰减和弛豫吸收之和代替声波总的衰减,并通过计算为该处理的合理性提供依据.在简化的DL模型基础上,与声速一起,建立了两个声学参数同混合气体浓度、温度的三维关系模型.结合提出的声学法多物理场重建算法,实现了CO-N2-O2混合气体二维空间温度场、浓度场及流场的同时重建,并确定了划分浓度和温度的最佳步长为Δt=0.1K,Δc=0.001.数值仿真结果表明该算法具有较高的精度,可以承受一定的噪声干扰,并具有在线监测的能力.同时可以将该算法应用到其他混合气体的测量,为混合气体的复杂多物理场测量提供了一种新的有效方法.





