
目前人们对航空乘坐舒适性和环境的要求越来越高,降低航空发动机噪声成为当前研究热点。随着航空发动机涵道比的增加,喷射噪声的降低,大风扇成为主要噪声源,其中动静干涉是最主要影响部分。动静叶的相互干涉使流场具有很强的非定常特性,尾迹、泄漏流等使得流场出现周期性变换,产生较大离散单音噪声;黏性作用引起的尾迹,在向下游传播中不断受到下游势流的影响,同时,由于动叶尾迹不断脱落扫过静叶,使得静叶表面出现非定常的压力脉动,会对静叶表面的边界层、涡脱落等产生影响,静叶表面的压力脉动是主要的噪声源。
在声学试验方面,文献[1-3]研究发现,通过合适匹配倾掠角以及静叶数目,可以显着降低一阶叶片通过频率(blade passing frequency)单音噪声和总声压级,对于单音噪声最大可降6dB.
在声学预测上,Ferrecchia等通过二维数值计算得到动叶尾迹在静叶通道的发展分布规律,进而对动静干涉噪声进行预测,结果表明单音噪声与动叶尾迹亏损速度大小以及尾迹的宽度有直接联系;Nark等采用经验公式,将噪声源分为动静叶、静叶尾迹近场、后管道区域分别进行预测,对远场和近场的一阶和二阶单音噪声预测结果较好;Peters等则首次将噪声源区分为动叶尾迹、静叶前缘势流、轮毂机匣二次流、以及叶顶泄漏流;Cooper等通过在旋流中对不同倾角、掠角的静叶进行研究,使用尾迹发展模型以及准三维片条理论,提出了一种渐进式声学预测方法以及尾迹干涉数学模型。
在获取动叶尾迹分布方面,Ottavy等通过粒子速度成像仪来获得尾迹脉动;Sentker等获得了一级半低压压气机中径位置S1流面以及不同S3流面的尾迹速度和湍流度的详细分布,研究了进口导叶尾迹在进入静叶通道后与动叶尾迹干涉的耦合作用;王英锋等通过在动静叶表面埋设压力传感器,获得动静叶表面的压力脉动,分析了动静间距对动静干涉的非定常作用;段肖珑通过对3种不同弯角的动叶进行动静干涉数值研究,得到了动叶尾迹在动静级间的发展历程,以及不同弯角的动叶对动静级间流场压力脉动强度的影响,并对其声学模态进行了相关预测。
本文采用试验和数值方法,分析不同倾角静叶对动静干涉的声学特性以及动静级间流场的影响。
声学测试得到静叶倾角为-25°~25°时动静干涉噪声谱,提取噪声谱中各阶单音噪声,得出倾角对单音噪声以及总声压级的影响;同时,对±25°和0°3种不同静叶倾角进行数值模拟,获得动静级间以及静叶的非定常特性,探讨倾角对静叶表面压力脉动的影响以及动静级间动叶尾迹的发展历程。
1 研究对象
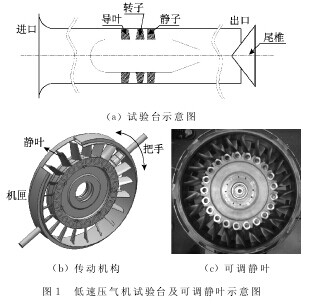
本文以上海交通大学1.5级低速低压轴流压气机为研究对象,压气机设计转速为3 000r/min,轮毂比为0.7,共有3排叶片、13个导叶、21个动叶和21个静叶。
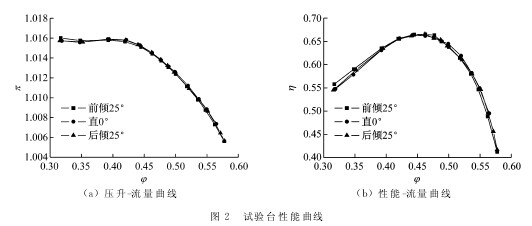
定义静叶积叠线与通过静叶转轴径向线的夹角为静叶倾角ξ;ξ<0时,定义为前倾,ξ>0为后倾(与转子转动方向相同),文中ξ∈(-25° 25°);ξ=0为直静叶。通过固定在机匣上的把手转动机匣从而带动静叶绕固定轴旋转调节倾角,试验台以及静叶倾角驱动机构如图1所示,图2为试验测得前倾25°,直0°,后倾25°的性能曲线。图中,π为压比,η为效率,φ为流量系数。由图可见,在低速情况下静叶倾斜对试验台整体性能曲线影响不大。【图1.2】
2 噪声测试及结果分析
限于试验台的尺寸太大,噪声测量在上海交通大学航空航天学院室外大空间进行,测试简图如图3所示。试验严格按照风机和罗茨鼓风机噪声测量方法GB/T 2888-2008进行,测点至声源点间距为1倍和2倍标准长度时,其A声压级的差值大于5dB(A),满足现场测量条件。麦克风与试验台转轴处于同一水平面,测点距离以动静交接面为圆心半径1m的圆上,麦克风位置角度θ为45°~135°。试验用麦克风型号为B&K 4189,不确定度为0.2dB,最大输入声压级为146dB,满足试验测试精度和量程要求,采集系统选用NI PXI 1033系列机箱及PXI-4472多通道数据采集卡。【图3】
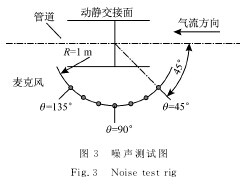
试验测试方案:ξ从-25°~25°每5°为1种方案,共11个;在压气机一侧从45°~135°布置7个麦克风,每个数据点重复测量7次。
图4所示为θ=120°时ξ=0°和ξ=20°的某次噪声测量频谱。图中,f为频率,SPL(Sound PressureLevel)为声压级。由图可见,随着ξ的增加,一阶单音 噪声出现了很明显的降低,约16.3dB,但是在二阶、三阶叶片通过频率(Blade Passing Frequen-cy,BPF)上则出现了增加,倾斜叶片对于一阶BPF的抑制效果很明显。【图4】
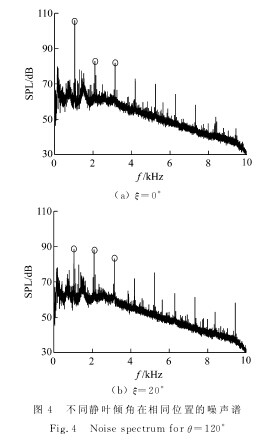
图5为声压级测量结果云图。宽频噪声SPL集中在102.9~103.9dB,总体变化很小;单音噪声最大出现在±10°倾角范围内,当倾角正负变化时,都使得单音噪声出现了相应程度的降低,单音噪声是总声压级的决定因素,并且使总声压级出现降低。图6为提取噪声频谱前三阶单音噪声云图。【图5】
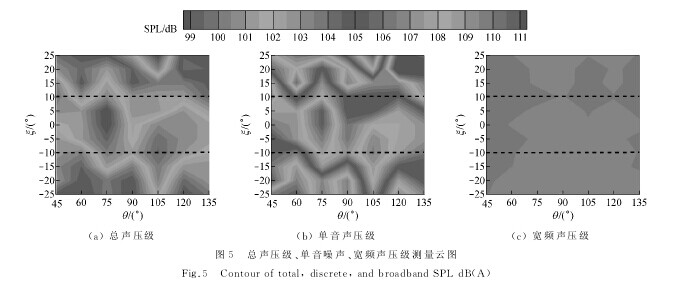
由图6(a)可见,它与单音噪声以及总声压的云图分布基本相同,可以认为导致总声压级不同的主要原因来源于一阶单音噪声,同样可以看出,通过倾斜静叶,使得二阶单音噪声也出现了降低,后倾静叶对于一阶、二阶单音噪声的降低效果要明显好于前倾。【图6】
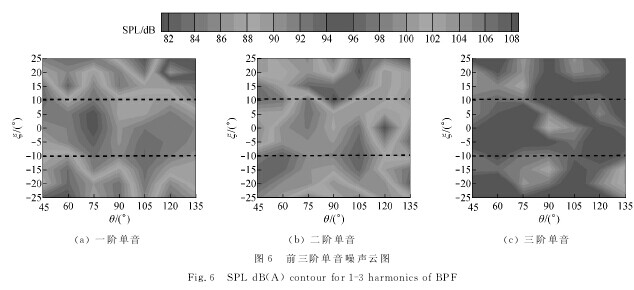
图7是总声压级减去宽频声压级的云图,即单音噪声使总声压级的增加值。在|ξ|<10°时,BPF使得总声压级的增加值都超过了4dB,其中,直静叶时单音噪声对总声压级的增加值最大;在|ξ|>10°时,随着ξ的增大,单音噪声使得总声压级的增加远小于|ξ|<10°时的值;可以看出,后倾ξ>10°的域值和范围要大于前倾ξ<-10°的,后倾对于单音噪声的降低效果更明显。
定义声压级b在总声压级c所占比例为αb_c=100.1b/100.1c=100.1(b-c)图8(a)是单音噪声所占比例αBPF_total,更为清晰地描述了单音噪声占总声压级的比例。在倾角|ξ|<10°区域,单音噪声对总声压级所占比率都要大于50%,在倾角0°更是到达大于70%.图8(b)是一阶单音噪声所占比例α1st_total.在|ξ|<10°时一阶单音噪声对总声压级的贡献甚至可达50%,在|ξ|>10°的大部分区域,一阶单音噪声所占比例降到30%以下,对于倾斜静叶降低一阶单音噪声的效果非常明显。通过调节ξ达到改变总声压级的目的,主要是通过降低一阶单音噪声来实现,后倾静叶的控制效果优于前倾。【图7.8】
3 数值计算及分析
3.1 数值方法
数值计算选3种静叶倾角,分别对应静叶倾角为ξ=-25°(前倾25°)、0°(直0°)、25°(后倾25°)。
为了降低计算量,将导叶数由13改为14并将其弦长缩小,保证稠度不变,叶片数比为导叶∶动叶∶静叶=2∶3∶3,采用8个通道进行计算。
本文采用H-O-H结构化网格,3种不同算例网格采用完全相同的拓扑结构和网格数,8通道共计380万网格节点,网格示意图如图9所示。【图9】
数值模拟计算采用NUMECA/FINE,湍流模型采用S-A模型,差分格式采用二阶迎风格式,四阶Runge-Kutta法迭代求解,采用多重网格技术进行求解。
非定常计算动静交界面采用Domain Scal-ing方法,使用双时间步,内时间步设置迭代步数为100,外时间步则把每个静叶栅距流道划分为64个时间步,对应物理时间步长约为Δt=1.488×10-5s,计算5圈各监控值均出现周期性波动。边界条件为进口轴向进气,总温293K,总压101.325kPa,出口给定静压,保证3种算例流量均为4.9kg/s,叶片表面和固体表面均采用无滑移边界条件和绝热壁面条件。
3.2 静叶表面的均方根压力脉动
根据FW-H方程,四极子和单极子源项在实际风扇和压气机中可以忽略,只剩下偶极子项,方程可以简化为【1】
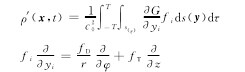
其中:ρ′为密度扰动;G为格林函数;x,y分别为观测点和声源坐标;t为观测点接声时间;T为叶片转动周期;τ为声源时间;c0为声速;s(τ)为叶片固体壁面;fi为叶片表面受到的非定常力;fT、fD分别为轴向推力和周向阻力;(r,φ,z)为叶片上圆柱坐标。
定义均方根压力如下:【2】
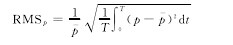
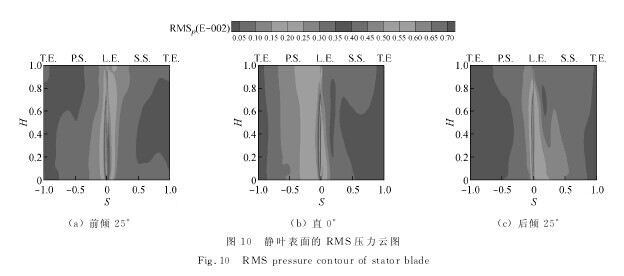
其中,p-为当地静压均值。图10所示为静叶表面的均方根压力脉动图。图中,纵坐标H为叶高,横坐标S代表以前缘为起点的叶片表面弧长,T.E.代表静叶尾缘,L.E.代表前缘,P.S.代表压力面,S.S.代表吸力面。
由图可见,直静叶的压力脉动集中于前缘附近的压力面,前倾和后倾静叶则集中于静叶前缘;相比与直静叶,后倾在扰动范围上出现了较大的降低,前倾静叶变化相对较小。所有静叶前缘的压力扰动最大,而且最大扰动区域出现在从叶根到近80%叶高靠近前缘压力面的区域。这是因为动叶尾迹区域的速度亏损造成尾迹扫过静叶前缘时进气角明显增大,使得前缘压力面一侧的静压显着升高,正冲角下前缘的绕流也使吸力面一侧的静压明显降低,因此造成了静叶前缘处静压的剧烈波动。【图10】
3.3 倾角对动叶尾迹的相位调节
为了捕获倾角对动叶尾迹形态的干扰,同时避免下游势流对动叶尾迹干扰过大,以静叶前缘为基准,沿z轴在离静叶前缘2mm的动静级间约85%的轴向位置布置一条监控直线L,如图11所示。【图11】

在L上从叶根到叶顶共布置65个监控点,其中点P对应监控线的中径位置。
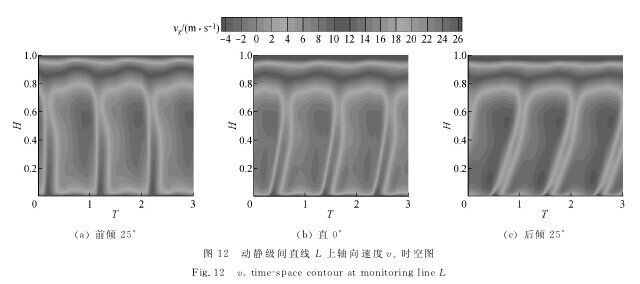
图12是L上轴向速度vz时空图。图中,T为时间周期。从尾迹发展历程可以看出,速度亏损区主要集中于80%叶高以下区域,前倾静叶使得尾迹相位发生了翻转,后倾使动叶尾迹在时间上实现了有效拉长,使得动叶尾迹扫过整个静叶的时间加长,由此尾迹作用在静叶上的脉动分布更为均匀,从而有效降低由于动叶尾迹造成的静叶压力脉动,这与RMS压力分布相符合。【图12】
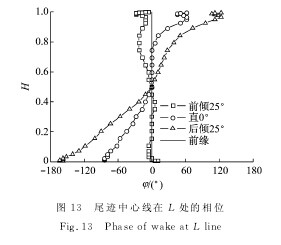
为了进一步说明不同倾角对动叶尾迹相位的调整作用,将监控直线L上的其他监控点与P点做互相关分析,可得动叶尾迹在L处的具体相位形态,如图13所示。图中,φ为相位。图中清晰说明了3种不同倾角动叶尾迹中心线的形态,其中正相位代表尾迹超前于中径处P点到达,负相位代表落后于P点。在直线L上,50%叶高以下区域前倾静叶的尾迹相位离静叶前缘线最近,在50%叶高以上区域直静叶最近;后倾静叶在尾迹相位正负上与直静叶保持一致,但是相位差出现了极大增加,尤其是在叶根和叶顶区域。
根据轴向速度的时空图,尾迹速度亏损区集中在80%以下叶高范围,前倾静叶在50%~80%叶高区域尾迹相位角要小于直静叶,在50%以下区域则要大于直静叶,后倾静叶在整个叶高范围内都实现了较大的尾迹相位偏转。
由此看出,通过调整静叶的倾角,能够通过静叶势流和级间旋流的干涉作用影响尾迹发展方向,从而达到对动叶尾迹相位的调整。尾迹相位拉长能够降低在动叶尾迹对静叶表面的脉动影响,从而降低静叶表面的非定常脉动力,后倾静叶对动叶尾迹的相位调整作用要优于前倾。【图13】
4 结论
本文对不同静叶倾角对动静干涉噪声的影响进行了噪声试验测试,并且针对3个特殊静叶倾角进行了详细数值计算.研究了下游静叶倾角对静叶表面的压力脉动以及对动叶尾迹相位调整的作用.声学测试以及数值分析表明:
(1)下游倾斜静叶对低速低压压气机的性能影响较小;(2)倾斜静叶能够有效降低动静干涉一阶单音噪声,后倾静叶的控制效果要优于前倾,宽频声压级基本保持不变;在静叶倾角±10°内单音噪声远大于宽频噪声,在倾斜静叶角度选择上应尽量避开该区域;(3)静叶表面压力脉动集中在前缘,动叶尾迹的速度亏损区集中在80%叶高以下范围,静叶的倾斜对动叶尾迹相位起到了较大的调整作用;前倾使得尾迹下半部更贴近静叶前缘,后倾则使得尾迹在相位上实现了有效拉长,后倾静叶对于尾迹相位调整要优于前倾,这与声学试验测量结果保持一致.
参考文献:
[1]Woodward R P,Elliott D M,Hughes C E,et al.Benefits of swept-and-leaned stators for fan noise re-duction[J].Journal of Aircraft,2001,38(6):1130-1138.
[2]Woodward R P,Gazzaniga J A,Bartos L J,et al.Acoustic benefits of stator sweep and lean for a hightip speed fan[J].AIAA Paper,2002-1034.
[3]Envia E,Nallasamy M.Design selection and analysisof a swept and leaned stator concept[J].Journal ofSound and Vibration,1999,228(4):793-836.
[4]Ferrechia A,Dawes W N,Dhanasekeran P C.Com-pressor rotor wakes and tone noise study[J].AIAAPaper,2003-3328.
[5]Nark D M,Envia E,Burley C L.Fan noise predic-tion with applications to aircraft system noise assess-ment[J].AIAA Paper,2009-3291.
[6]Peters A,Spakovszky Z S.Rotor interaction noise incounter-rotating propfan propulsion systems[J].Journal of Turbomachinery,2012,134(1):011002.
[7]Cooper A J,Peake N.Rotor-stator interaction noisein swirling flow:Stator sweep and lean effects[J].AIAA Journal,2006,44(5):981-991.





