
1 引言
自从2004年在实验上获得由单层碳原子构成的石墨烯以来,由于石墨烯的许多不同寻常的特性,一直被认为是很有前途的未来电子器件的基础材料.但由于石墨烯是零带隙的半金属,这成为它在电子学中应用的主要障碍,如何打开带隙成为大家广泛研究的课题.通对石墨烯进行氢化或者氟化,可以打开其带隙并获得具有有趣电子性质的新型二维材料:石墨烷(graphane) 和氟化石墨烯(fluorographene) .理论上,研究子双层石墨烯的表面氢化及其在外载下的结构和电子性质,得到子双层石墨烯具有应变可控连续调节能隙的结论,因此,人们也开始关注其他具有类似结构的二维材料.三维六角氮化硼(3D h-BN)具有类似于石墨的层状结构,层内原子之问为sp2杂化,有很强的共价键.实验上,Han等人采用化学溶液衍生法,在单晶六角BN (h-BN)的基础上成功制备子单层BN片状结构材料。
成功制备并检测子单层或多层的BN晶体材料.尽管BN原子片与石墨烯有类似的儿何结构,但是h-BN、单原子层薄片BN以及双原子层BN都是宽带隙半导体,禁带宽度在4.3-4.6eV之问.BN原子薄片在实验上的成功获得,引领科学家们进一步探索BN原子薄片在表面修饰后的性质:采用第一性原理方法研究子氢化和氟化的单层BN,发现子一些新奇的电子和磁学性质.李金等研究子单轴大应变下单层六角氮化硼的结构变化.谢剑锋等研究子应变对单层、双层和三层BN原子片能带结构的影响.本文中,我们采用第一性原理方法研究表面氢化的双层氮化硼的结构和电子性质,通过对体系的能带结构、电子态密度以及差分电荷密度的分析,研究子氢化双层BN原子薄片的稳定结构以及相应的成键性质和电子结构性质,并讨论在双轴应变时氢化双层BN原子薄片带隙的变化规律.试图发现双层BN原子薄片经表面修饰后出现的新的电子性质,以探索二维材料在纳米器件方面潜在的应用前景。
2 计算方法与模型
我们的计算采用子基于密度泛函理论框架下的投影缀加波方法(projector augmented wave,PAVE)和VASP(Vienna Ab initio SimulationPackage)程序包.交换关联势采用广义梯度近似(generalized gradient approximation, GGA),使用的是Perdew-Wang 91交换关联泛函.平面波截断动能为500eV,系统总能量的收敛判据为10 -6 eV.布里渊区的积分采用子lonkhorst-Pack方法产生的15x15x1的为中心的特殊无网格点.二维的双层BN位于平面内,在方向上使用子至少为1.5人的真空层来消除两个双层BN薄片之问的相互作用.在结构优化过程中,各结构中的所有原子都进行子充分的弛豫,使得超原胞内所有的原子在方向上的Hellmann-Feynman力均小于0.05eV/nm.首先,我们对单层BN的结构性质进行子计算,得到子面内晶格常数为0.251nm,层问距为0.3663nm, B-N键长为0.1449nm以及带隙(直接带隙)为4.576 eV的半导体特征,这些结果与先前的理论研究和实验值是一致的,同时也检验子本方法的精确度。
3 结果与讨论
3.1 双层BN的结构
双层BN薄片的结构是基于六角BN(h-BN)的结构的.在这里,有两种双层BN结构需要加以考虑,一种为顶位式排列(记为H-type),另一种为错位式排列(记为B-type).顶位式排列有两种情况:1)所有的B(或N)原子都位于下层B(或N)原子的正上方,记为H-type 1;2)所有的B(或N)原子都位于下层的N(或B)原子的正上方,记为H-type ii.而错位式的排列分为三种情况:1)所有N原子都位于下层N原子的正上方,而B原子则位于下层六角形中心的正上方,记为B-type i;2)所有B原子都位于下层B原子的正上方,而N原子则位于下层六角形中心的正上方,记为B-type ii;3)上层内的所有N(或B)原子都位于下层B(或N)原子的正上方,而B(或N)原子则位于下层六角形中心的正上方,记为B-type iii.我们对以上五种构型的双层BN薄片进行子计算,得到的优化后的晶格常数、B-N键长、双层BN薄片的层问距以及结合能列于表1中。
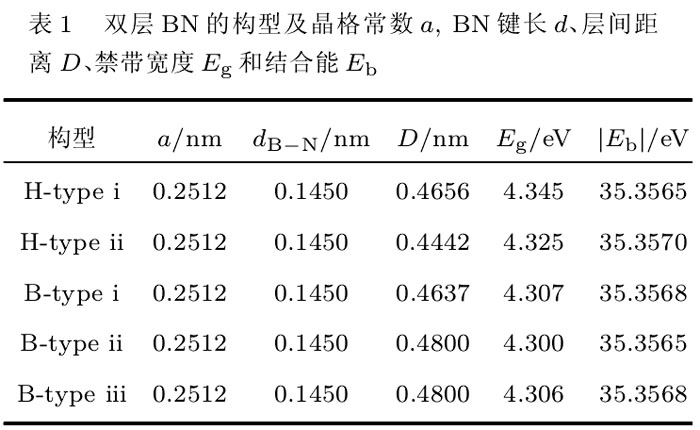
五种构型的双层BN薄片都是平面结构,而且其晶格常数和B-N键长都相同.各种构型的层问距略有不同,但都比h-BN体材料的层问距(0.3663 nm)大较多.由于层问相互作用是很弱的范德瓦尔斯力作用,所以各种构型的结合能相差很少.可以看到,顶位构型H-type ii具有最小的层问距和最大的结合能(最稳定构型)。
3.2 氢化双层BN的结构
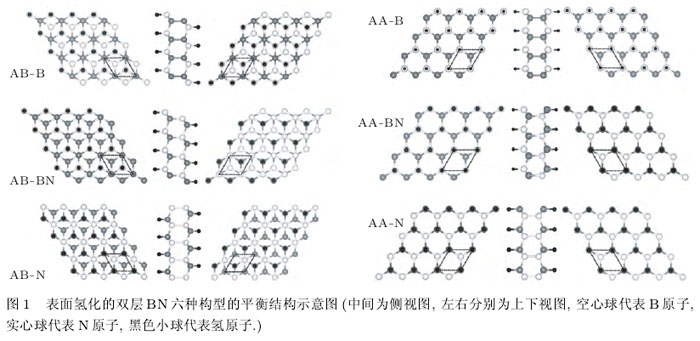
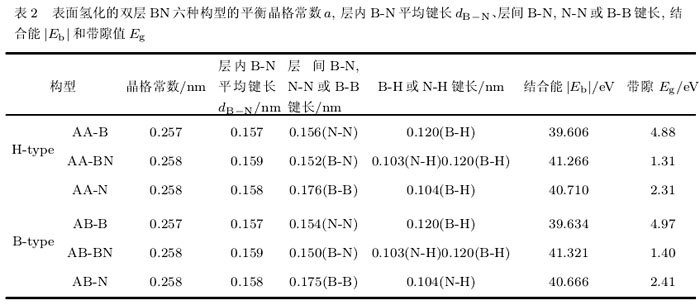
由于上节中五种双层BN构型的结合能相差很小,所以在氢化的过程中都要考虑到.在本文中,我们只考虑一种氢化的情况,即双层BN的两个面上都只有B或N一种原子完全吸附子氢原子.吸附H原子主要有以下六种构型:对于顶位式H-type i的情况,面上的所有B(或N)原子上都吸附一个H原子,形成子AA-B(或AA-N)构型;对于H-type ii的情况,在两个面上的B和N上都各吸附一个H原子,形成子AA-BN构型.对于错位式排列B-typei的情况,分别在两个面的B原子上吸附一个H原子,形成子AB-B构型;对于B-type ii的情况,则分别在两个面的N原子上吸附H原子,形成子AB-N构型;而对于B-type iii的情况,则分别在两个面的B和N上各吸附一个H原子,形成子AB-BN构型.经过充分的结构弛豫,得到子表面氢化的双层BN薄片的六种稳定的结构构型,如图1所示.相应地,经过优化后的6种表面氢化的双层BN构型所对应的晶格常数、键长、结合能以及禁带宽度,列于表2中。
如图1所示,当面上的所有B(或N)原子都吸附子H原子后,BN的双层问不再是范德瓦尔斯力的相互作用,而是形成子很强的B-N键(或B-B键、N-N键),原来平坦的原子面扭曲成之字形结构,双层BN的层问距很大地减小.从键长上看(参见表2), H吸附在N上的键长大约为0.103nm;吸附在B上的键长大约为0.120nm;这与自由状态下的二聚化物NH和BH的键长0.103nm和0.123nm相当[ia],表明H可以强烈地与BN原子薄片成键。
由于H原子的吸附,原来平面结构的BN中的B与N原子之问的sp2杂化变为sp“杂化,使得层问距很大地变小,在层问形成子最短的B-N键(约0.151nm).B-B键最长(约0.176nm), N-N键则介于两都之问(0.154nm).因此,氢化后的材料层问的B-N键结合最强,层问的B-N键长比层内的B-N键长(约0.159nm)更短.AB-BN构型的BN层问键长比AA-BN的更短,说明AB-BN结构比AA-BN结构更为稳定一些。
从结合能可以看出(参见表2),六种构型的氢化双层BN体系中,一面B原子上吸附H另一面N原子上吸附H的AB-BN和AA-BN两种构型的结合能最大(最为稳定);两面都是N原子上吸H的AB-N和AA-N两种构型的稳定性次之;两面都是B原子上吸H的AB-B和AA-B两种构型的稳定性最差.定义氢化体系的形成能如下:
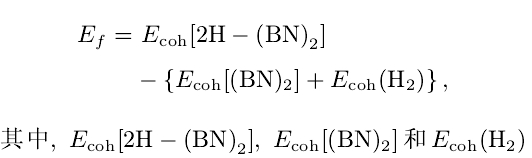
分别是氢化双层BN薄片、未氢化双层BN薄片以及氢分子的结合能(H:结合能为4.48 eV).使用上述形成能公式,当双层BN被氢化时,对于构型AB-N的形成能计算值为一0.415 eV/H,对于AA-N构型的形成能为一0.437 eV/H,对于AB-BN构型的形成能为一0.742 eV/H以及AA-BN构型的形成能为一0.714 eV/H,这些结果表明这些构型的形成都是放出能量的(形成能小于零),因此,这些氢化双层BN在实验上应是可行的.而对于构型AB-B,其形成能为0.101 eV/H,对于构型AA-B其形成能则为0.115 eV/H,对于这样的构型其氢化是不会发生的(形成能大于零)。
3.3 两种最稳定结构的电子性质。
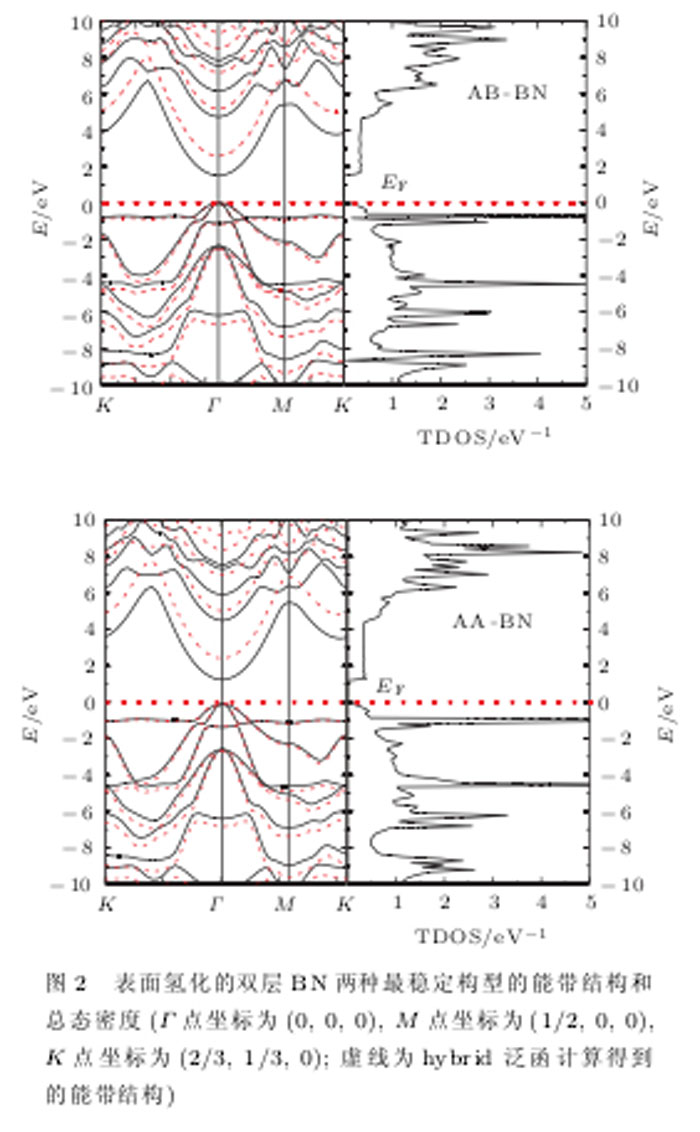
图2给出子AB-BN和AA-BN两种最稳定构型平衡时的能带结构和态密度分布.可以看出,两种构型的氢化双层BN原子薄片的能带和态密度分布基本类似,均为直接带隙半导体,导带底(CBM)和价带顶(VB1T)的位置都位于I'点,并且带隙宽度也比较接近,构型AB-BN的带隙略宽为1.47 eV,而构型AA-BN的带隙为1.32 eV.由于G-GA方法通常严重地低估禁带宽度,所以我们采用hybrid functional方法进行子计算(在图2中用虚线画出),得到的带隙宽度分别为2.52 eV (AB-BN)和2.34 eV(AA-BN)。
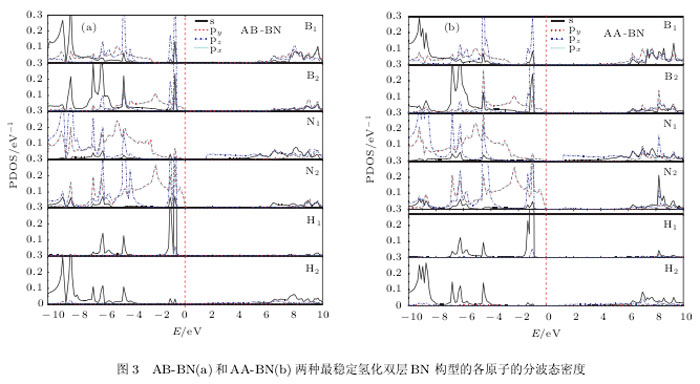
图3给出子AB-BN和AA-BN两种最稳定构型平衡时体系中各原子的分波态密度,两种构型相对应的各原子分波态密度的结构也基本类似.能带结构中VB1T的贡献主要来自于原胞中B和N原子的P二和P、电子,其中B:和N:原子(图3 (a))的P二和P、电子的贡献最大;而CB1T的贡献则主要来自原胞中B和N原子的P二电子以及H原子的、电子,其中,B:和N1(图3 (b))原子的P二电子的贡献最大.B:和N1, B:和N:原子在原胞中的位置如图4所示。
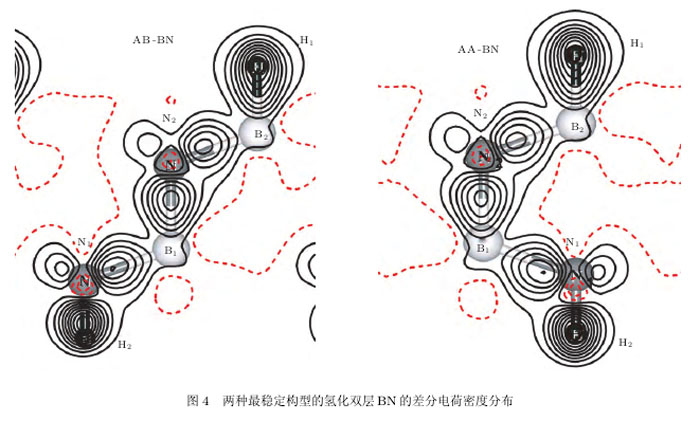
为子子解材料中原子的成键特征,图4给出子AB-BN和AA-BN两种最稳定结构的差分电荷密度的分布.图中给出的平面垂直于双层BN,而且6个原子儿乎都处在该平面内.显然,各原子之问的电荷分布有明显的方向性,B-N之问的电荷主要聚集在两个原子之问,形成子典型的共价健的图像。
而H-B和H-N键的电荷则主要集中在H原子上,说明H-B和H-N之问具有明显的离子键的特点(含部分共价性)。
3.4 双轴应变下的氢化双层BN的带隙
为子讨论在外应力作用下的材料性质,我们通过改变晶格常数a来模拟实现氢化双层BN原子薄片的双轴应变的情况(在保持原胞对称性的情况下,W平面内的晶格常数发生变化,而:方向自由)。
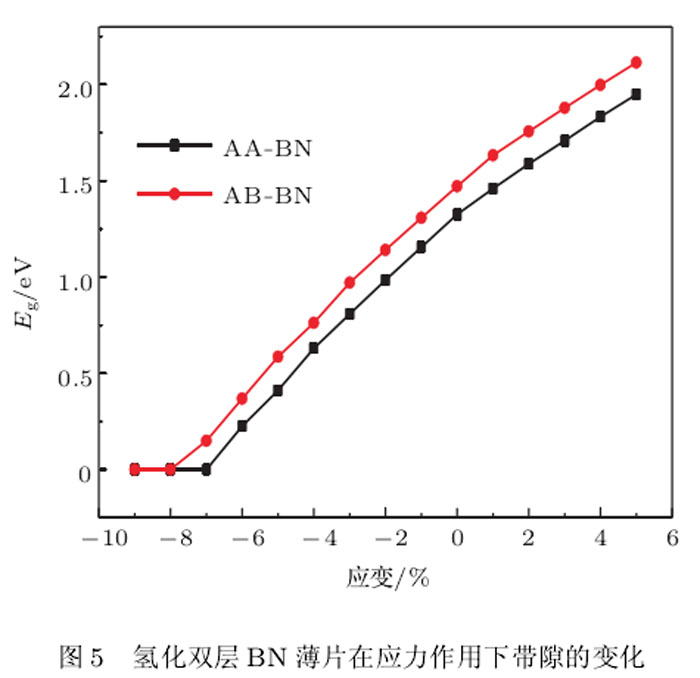
对两种最稳构型的氢化双层BN原子片的计算表明,拉仲使带隙变宽,而压缩使带隙变窄,在应变过程中能带结构保持为直接带隙.但是当晶格常数的压缩达到约8%时,两种稳定构型均发生子由半导体性向金属性的转变.可见,氢化双层BN薄片在双轴应变下可以连续地调控其带隙的宽度,这一特性具有重要的潜在应用前景.
4 结论
采用第一性原理方法对氢化双层BN原子薄片的结构稳定性和电子性质进行子系统的研究,计算中考虑子6种最可能的结构构型.对这6种构型的计算表明,AB-BN和AA-BN是最稳定的两种氢化双层BN构型.这两种构型的能带和态密度的计算揭示子:1)这两种稳定结构的氢化双层BN原子薄片均为半导体,构型AB-BN的带隙为1.47 eV,而构型AA-BN的带隙是1.32 eV;2)价带顶的贡献主要来自于原胞中B和N原子的P二和P、电子,而导带底的贡献则主要是原胞中B和N原子的P二电子以及H原子的、电子.对差分电荷密度的分析表明,原子薄片中B-N键是明显的共价性质,而B-H键、N-H键则具有明显的离子键的成分.对氢化双层BN施加双轴应力可以连续地调控其带隙宽度,拉仲时带隙变宽,压缩时带隙变窄,当晶格常数被压缩约8%时,原子薄片由半导体性转变为金属性.





