雨果·索南夏因对微观经济理论的贡献
摘要:雨果·索南夏因是美国杰出的经济学家, 重点研究一般均衡理论, 并因为索南夏因-曼特尔-德布鲁定理而享誉学术界。他的主要贡献包括: (1) 率先对超额需求函数结构进行研究, 对索南夏因-曼特尔-德布鲁定理的提出有重要贡献, 证明了满足特定限制的任意函数都可能是经济体的超额需求函数, 此时均衡不唯一且不稳定。这一成果表明了一般均衡理论的不可证伪性, 也带来了微观经济学基础和宏观经济学的分离。 (2) 提出了价格机制的公理化表达方式, 塑造了价格的识别机制, 为公理化表达社会选择过程做出了突出贡献。 (3) 通过放松阿罗不可能定理的基本假设、简化吉伯德-萨特思韦特定理的证明和研究防止策略性的机制, 推动了投票理论的发展。 (4) 对鲁宾斯坦讨价还价模型进行了扩展与再检验, 将不完全信息情境引入讨价还价模型中, 使该模型更具现实解释力。
关键词:索南夏因; 一般均衡; 投票; 价格公理化; 非合作谈判;
作者简介:姚东旻, 电子邮箱:yaodongminn@163.com; 庄颖, zhuangy1993@163.com; 朱泳奕, zhuyongyii@163.com。;
基金:中央高校基本科研业务费专项资金;
Hugo F. Sonnenschein's Contributions to Microeconomics
YAO Dongmin ZHUANG Ying ZHU Yongyi
Central University of Finance and Economics
Abstract:Hugo F. Sonnenschein, with microeconomics as his main research area, is an outstanding economist in the United States. He focuses on general equilibrium theory and is famous for Sonnenschein-Mantel-Debreu theorem. His main contributions are as follows: Firstly, Sonnenschein takes the lead in analyzing the structure of excess demand function, and proposes the Sonnenschein-Mantel-Debreu theorem, which proves that any function satisfying certain limits may be the excess demand function of the economy. The theorem shows that the equilibrium is non-unique and unstable, which further leads to the unfalsifiablity of general equilibrium theory, and brings also the separation between the micro-foundation and macroeconomics. Secondly, Sonnenschein presents the axiomatic characterization of the price mechanism, distinguishing it from other competitive mechanisms, and promotes the axiomatization of the social selection process. Thirdly, Sonnenschein enriches the voting theory by relaxing the fundamental assumptions of the Arrow's impossibility theorem, simplifies the proof of Gibbard-Satterthwaite theorem, and explores the mechanism of strategy-proofness. Fourthly, Sonnenschein extends and re-examines the Rubinstein bargaining model, by introducing bargaining under incomplete information into the model, which makes the bargaining model more realistic.
Keyword:Hugo F. Sonnenschein; Sonnenschein-Mantel-Debreu Theorem; General Equilibrium; Price Axiomatization; Non-cooperative Bargaining;
雨果·索南夏因 (Hugo F. Sonnenschein) 是美国杰出的经济学家与教育管理者, 曾任芝加哥大学校长, 现任芝加哥大学讲席教授。索南夏因1940年11月14日出生于美国纽约。他于1961年获罗切斯特大学数学学士学位, 1964年获普渡大学经济学博士学位。索南夏因毕业后曾先后执教于明尼苏达大学、马萨诸塞大学和西北大学;自1976年起开始任普林斯顿大学经济系教授;1988—1991年间任美国宾夕法尼亚大学文理学院院长和讲座教授;1991—1993年再任普林斯顿大学讲席教授, 并任该校教务长;1993年起任芝加哥大学讲席教授, 并于1993—2000年任该校校长。索南夏因曾先后当选为美国艺术和科学院院士、美国国家科学院院士、经济计量学会会长、美国哲学学会会士、美国经济学联合会杰出会士。
索南夏因的研究极大地促进了微观经济理论的发展。他重点研究一般均衡理论, 并因为与曼特尔 (R.Mantel) 和德布鲁 (G.Debreu) 共同提出的索南夏因-曼特尔-德布鲁定理 (Sonnenschein-Mantel-Debreu theorem, 简称SMD定理) 而享誉学术界。该定理表明:满足连续性 (continuity) 、零次齐次性 (zero homogeneity) 并遵循瓦尔拉斯法则 (Walras's law) 的任何函数, 都可能是超额需求函数。此时, 经济体中存在多重均衡且无法保持稳定状态, 这导致了一般均衡理论不可证伪。总超额需求函数仅有的三个限制条件降低了一般均衡理论对个人理性行为的解释力, 带来了微观经济学基础和宏观经济理论间的不匹配。除了对一般均衡理论的贡献外, 索南夏因还通过公理化的方式表达价格机制, 并通过规范性的分析框架探索市场中消费者行为和厂商行为的动态变化, 促进了社会选择过程中公理化范式的应用。同时, 索南夏因通过对阿罗不可能定理的拓展和对吉伯德-萨特思韦特定理 (Gibbard-Satterthwaite theorem, 简称G-S定理) 的简化, 丰富了防止独裁性和防止策略性的研究。而其对鲁宾斯坦讨价还价模型的延伸和再检验, 增加了该模型的适用性与解释力, 使得索南夏因在非合作谈判的研究领域占有一席之地。下文将对索南夏因在上述四个方面的研究进行详细的介绍。
一、索南夏因对一般均衡理论的贡献
索南夏因对一般均衡理论发展的核心贡献, 是其与曼特尔 (Mantel, 1974) 、德布鲁 (Debreu, 1974) 共同证明的SMD定理。本节我们将以一般均衡理论的发展为线索, 阐述SMD定理产生的背景及其主要内容, 并深入分析其对一般均衡理论可证伪性的挑战和对一般均衡理论后续发展的影响。
(一) 一般均衡理论及其发展
一般均衡理论是在对经济主体偏好、技术和禀赋的基本假设下, 建立的关于人类经济系统整体均衡的存在性、稳定性和有效性的公理化研究理论, 在西方经济学中起到了支柱作用。早在古典经济学时期, 学者就对“均衡”概念有了科学的初步认识。当时的“均衡”是指经济社会以时间为维度, 在经历冲击之后恢复到的平衡状态。瓦尔拉斯最早在《纯粹经济学要义》 (Walras, 1874) 中建立起一般均衡模型, 研究市场经济中消费者和厂商间的相互关系, 并运用消费者效用最大化、厂商利润最大化和市场出清等条件对市场行为进行规范和限制。当经济体在一组价格中实现了供给和需求的平衡, 且该组价格保持不变时, 经济体处于均衡状态。
瓦尔拉斯通过构建独立方程求解经济中的均衡。他认为如果方程是线性、独立、不受限制的, 且方程个数与未知数个数相同, 则存在均衡解。然而, 方程通常是非线性的且需要满足更多的限制, 从而无法保证均衡解的存在。因此, 之后的学者专注于一般均衡存在性的证明。其中, 阿罗和德布鲁 (Arrow & Debreu, 1954) 首次利用超额需求函数对一般均衡理论进行严格叙述, 并在满足特殊的前提条件下, 给出了均衡存在性的数学证明, 即瓦尔拉斯一般均衡方程组在某些特殊假设下有解, 这就是着名的“阿罗-德布鲁模型”。德布鲁 (Debreu, 1959) 证明了, 在个人偏好关系满足连续性、严格凸性 (strictly convex) 和严格单调递增 (strictly monotonically increasing) 的条件下, 超额需求函数是市场价格的连续、零次齐次且满足瓦尔拉斯法则的函数。在此基础上, 学者通过构建整体经济的总超额需求函数来讨论均衡的存在性问题 (Sonnenschein, 2017) 。
然而, 仅仅证明经济体中存在均衡是远远不够的, 还需要证明该均衡是唯一确定且保持稳定的。虽然阿罗等经济学家充分讨论了此问题, 但除了均衡存在性外, 均衡唯一性、价格调整的全局稳定性和比较静态只在极其严格的条件下才成立。因此, 这些工作无法得出具有普适性的结果, 仍然有许多问题需要继续讨论。例如, 一个定义在正象限 (positive orthant) 内部紧集 (compact set) 上的函数能否作为一般经济均衡的超额需求函数?线性的超额需求函数在理论上是否存在?要想回答这些问题, 需要对超额需求函数的结构进行更加深入的研究。遗憾的是, 当时学术界对超额需求函数的研究仅仅停留在经验统计层面, 直到1972年5月, 索南夏因才首次对超额需求函数的结构进行了分析。
(二) SMD定理的提出
超额需求函数是经济中各个经济主体的超额需求之和, 由经济主体的偏好关系、禀赋以及市场价格所决定, 是研究均衡及其性质的有效途径。索南夏因 (Sonnenschein, 1972, 1973) 认为, 在证明均衡唯一性时, 应该首先考虑经济体中可能存在什么类型的超额需求函数, 从而将均衡解的唯一性问题转化为超额需求函数的唯一性问题。
索南夏因 (Sonnenschein, 1972) 率先思考在正象限内部, 特定商品的超额需求函数是否存在于一般均衡经济中。其研究结果表明: (1) 在相对价格域中, 任意一个多项式函数都可能作为特定商品的超额需求函数; (2) 对于相对价格域中的任何价格, 当且仅当它满足瓦尔拉斯法则时, 能够基于该价格生成任何给定的超额需求分配。
索南夏因 (Sonnenschein, 1973) 随后证明了德布鲁1959年研究结果的逆命题。他指出: (1) 如果一个行为良好的交换经济的总超额需求函数能够将价格映射为数量, 这个函数必须满足连续性、零次齐次性和瓦尔拉斯法则。 (2) 当经济中只存在两种商品时, 对于任何一个满足上述三个条件的超额需求函数, 总能够通过个人效用最大化的方式生成对应的经济体, 即超额需求函数可逆。
在此之后, 曼特尔 (Mantel, 1974) 和德布鲁 (Debreu, 1974) 进一步证明了在任意种类商品和存在L个位似消费者 (对初始禀赋配置无任何限制) 的情形下, 总超额需求函数的性质, 最终形成了索南夏因-曼特尔-德布鲁定理 (即SMD定理) 。该定理表明, 当相对价格变化时, 个体禀赋价值也随之发生变化, 但总超额需求函数并不继承个体超额需求函数的所有属性。这使得经济体总能在特定条件下基于价格实现超额需求配置, 此时一个经济体中存在多个超额需求函数, 而任何一个满足特定条件的超额需求函数也都能构建出对应的经济体。总超额需求函数的不唯一性使我们没有理由要求经济体中均衡是唯一的且稳定的。此时, 任何满足SMD定理限制的事都会发生 (Mas-Colell et al, 1995) , 后人也将SMD定理称为“一切皆有可能定理” (anything goes theorem) 。
(三) SMD定理对一般均衡理论的挑战
一般均衡理论作为经济学支柱是无可争议的, 但SMD定理的提出在很大程度上削弱了一般均衡理论的已有成果。限制条件的任意性、均衡点的多样性和全局的不稳定性, 使得经验事实不能对一般均衡理论进行检验, 这对一般均衡可证伪的观点产生了相当大的冲击 (Shafer & Sonnenschein, 1982) 。面对市场经验事实, 总能找到多个总超额需求函数, 既能反映现实数据的特征, 又符合一般均衡理论的限制要求。从市场经验的“一”, 到总超额需求函数的“多”, 再到一般均衡理论的“一”, 形成了“条条大路通罗马”的情况。任何经验事实都能在一般均衡理论的范围内得到解释。Carvajal et al (2004) 认为该现象表明一般均衡理论存在不足, 即一般均衡理论不能产生可经验证伪的预测。
就唯一性来看, 在经济竞争模型中主要通过求解数学模型确定经济体系的状态, 方程的解就是经济的均衡 (Kehoe, 1985) 。保证均衡的唯一性是应用比较静态分析的关键。当个体超额需求函数满足显示偏好弱公理 (weak axiom of revealed preference) 或总可替代性 (gross substitutability) 时, 纯交换经济存在唯一的均衡。但SMD定理认为, 单独的个体偏好不足以确定经济将处于哪个均衡, 多个超额需求函数的存在会求解出多个均衡解。均衡的多重性表明, 在具体应用中, 全局的比较静态分析不再有效, 我们难以确定均衡处在哪种具体的状态中。因此, 也就无法对一般均衡理论能否准确、有效预测经济状态进行检验, 这弱化了一般均衡理论的解释力和预测力。
就稳定性来看, 稳定性的解决方案为进行比较静态分析提供了重要的支撑 (Samuelson, 1941) 。稳定性探讨当初始价格不是均衡价格时是否存在价格调整过程使价格向均衡点收敛。然而, 并非所有的动态系统都是稳定的, 当价格动态调整过程无法使经济趋向均衡时, 就无法实现全局稳定 (Tohme, 2006) 。给定总超额需求函数的性质, 可以构建一个反映竞争过程的动态模型来考察其是否具有稳定性质。该模型的二阶偏导数条件是保证局部稳定均衡存在的条件, 描述价格动态的微分方程等价于超额需求函数或与超额需求函数成比例。SMD定理意味着, 对于每一个给定的均衡价格体系和相关的超额需求, 都可以定义出任意拥有相同总体行为和相同均衡的经济体。超额需求函数的任意性使得二阶偏导数条件也具有任意性, 很容易产生局部不稳定和背离均衡轨迹的超额需求矢量, 导致全局不稳定性 (Ingrao & Israel, 1990) 。SMD定理使全局不稳定的例子得到扩展, 我们很难准确预测未来会发生什么, 将朝着哪个方向发展, 也无法通过经验事实对未来的不确定性进行评判, 这对一般均衡理论在稳定性上的发展产生了重大影响。
事实上, 一般均衡理论的很多假设只是对现实世界的粗略数学表示, 不仅概念界定过于宽泛和模糊, 且缺少能够获得确定经济结论的基本假设。这使得一旦面对经济中可能出现的任何有悖于一般均衡理论的经验事实, 一般均衡理论都可以通过: (1) 对概念的进一步细化将该情况纳入一般均衡理论的解释范围 (Kirman, 1989) ; (2) 构造一个满足一般均衡理论基本条件的经济体, 使得在该经济体中特殊的经验事实能够得到合理解释。可见, 总超额需求函数的无限可能使我们无法找到经验事实来反驳一般均衡理论, 理论的科学性也就无从谈起了。正如索南夏因等 (Shafer & Sonnenschein, 1982) 指出, 一般均衡理论本质上没有对数据施加任何可验证的限制。SMD定理对一般均衡存在可证伪限制的挑战, 直接导致了该理论被很多学者质疑甚至是遗弃。
(四) 索南夏因对一般均衡理论后续发展的重大影响
SMD定理对一般均衡理论的挑战使得许多学者希望通过个体偏好假设来预测市场需求的愿望破灭。众多经济学者开始质疑一般均衡理论的中心地位, 这导致了研究一般均衡理论的学者们的分道扬镳:一部分学者试图通过改变一般均衡理论的条件, 恢复其理论有效性, 例如加强对偏好和个人行为等的具体限制, 以及运用均衡流形 (equilibrium manifold) 1替换超额需求函数等;而另一部分学者则通过建立宏观与微观的联系, 消除一般均衡理论微观基础和宏观理论分离的现象, 如理性预期理论对不确定情形下竞争性均衡的证明等。以下对一般均衡理论的后续发展进行详细介绍。
1.对一般均衡理论可证伪性的再讨论。
“一切皆有可能定理”并不意味着经济学理论的终结 (Sonnenschein, 2017) 。如果期望总超额需求函数表现出特定的特性, 就需要对个人如何与其他人相联系做出限制。然而, 即使要求初始禀赋分布是一组事先确定的商品空间中的独立点, 或者对消费者偏好施加同质性的较强假设, 也不会改变SMD定理的有效性 (Cheng & Wellman, 1998) 。因为在SMD定理的模型构建中, 允许为所有的个体选择相同的禀赋条件。因此, 增加对代理人同质偏好、相对收入分布任意设定等限制并不会影响超额需求函数的性质。Kirman (1989) 尝试从消费者个体间的特征出发对个人需求行为进行限制, 要求个体行为相互依赖或具有共同一致行为。在该假设下, 市场中个体之间的联系才能导致总体层面的规律性, 进而对总超额需求函数施加有意义的限制。同时, 对代理人分布特征的假设, 例如收入分配导致的富人和穷人的比例、社会组织的演变所代表的一部分人的利益诉求, 也能带来对总需求函数的合理解释, 进而解释宏观规律性。
更进一步地, 部分学者直接运用均衡流形替代总超额需求函数, 跳出了原有的思维框架。在显示偏好公理、瓦尔拉斯对应 (Walrasian correspondence) 等技术支持下, 均衡流形能够实现对均衡的比较静态分析, 成为研究一般均衡理论新的基础。Brown & Matzkin (1996) 认为, 在没有对个人选择行为进行观察的基础上, 个人的理性信息能够对总体变量施加限制。Chiappori & Ekeland (2004) 支持该观点, 给定一个从总禀赋到价格的光滑映射, 在假设经济中存在至少和商品数量相等的消费者的前提下, 对于某些个人效用函数和完全平等的总收入分配, 不能拒绝存在从总禀赋到均衡价格的映射函数的假设。该映射函数正是均衡流形, 通过引入私人收入或禀赋信息, 采取了另一种从市场行为到一般均衡理论的对应路径。
2.对微观基础和宏观理论关系的重新诠释。
部分学者仍然坚持认为, 一般均衡模型没有可证伪的经验事实, SMD定理对超额需求函数的分析给一般均衡理论带来了“灭顶之灾” (Hahn, 1975) 。这导致近年来越来越多的研究认为瓦尔拉斯微观经济学已经走向没落, 应该从经济研究的前沿转移到幕后。一般均衡理论在对经济体中个人行为性质的分析基础上构建模型, 并通过总超额需求函数的性质确定经济中均衡的性质。例如, 通过行为良好 (well-behaved) 的代表性代理人 (representative agent) 的选择或偏好反映出社会的总体选择, 使对个人消费者需求性质的研究能够在整体层面同样适用。这导致了当时存在微观经济学和宏观经济学都能解释宏观总体现象的局面。然而SMD定理的提出隔断了个人需求函数和总超额需求函数的对应关系, 即使经济中的每个个体都很好地满足了需求函数的所有基本条件, 在对个人需求进行加总时, 类似显示偏好弱公理等重要条件也会变得不满足。这导致加总市场行为的任意模型都不适用。此时, 微观经济学无法为宏观经济学提供理论基础 (Hands, 2012) , 从而微观经济基础和宏观经济理论相互分离。
这催生了学者关于建立宏观和微观相互关系的新尝试, 理性预期理论开始取得发展。一方面, 宏观经济政策主要是通过影响微观个体行为实现的, 仅仅根据宏观经济形势制定政策会缺少微观基础上的支持。另一方面, 微观个人通过整合私人信息和市场信息, 形成了对未来经济形势的理性预期并影响宏观经济变量。理性预期的分析方法将微观分析与宏观分析相结合, 使研究不确定情形下的一般均衡问题成为可能。市场中的交易在很大程度上是随着时间的推移而先后发生的, 索南夏因等 (Anderson & Sonnenschein, 1982) 证明了当代理人的预期满足理性条件时, 存在不确定情境中的竞争性均衡。随后, 索南夏因等 (Anderson & Sonnenschein, 1985) 将价格、私人信息和环境状态结合起来构建一般均衡的计量模型, 并通过模型估计数据和真实市场数据的比较对不确定情形下的一般均衡理论进行了验证。
二、索南夏因对价格机制研究的贡献
价格机制在经济学研究中占有重要的地位。亚当·斯密“看不见的手”指出, 即使市场中个人独立进行最大化决策, 最终也能达到整体均衡。在此过程中, 价格机制发挥了重要的作用。当市场处于非均衡状态时, 价格机制通过调整资源配置达到市场出清。当经济处于均衡状态时, 商品的总供给和总需求取决于市场上所有商品和要素的价格, 此时使商品市场和要素市场同时达到均衡的价格即为均衡价格。在均衡唯一性和稳定性的探索中, 价格机制是保证全局稳定的重要手段。因此, 索南夏因对价格机制给予了高度的关注和热情。
图1 索南夏因对价格机制的贡献
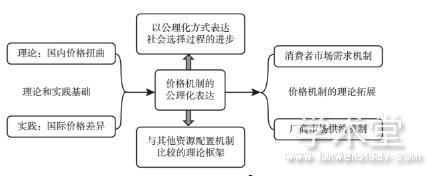
图1 索南夏因对价格机制的贡献 下载原图
索南夏因等 (Krueger & Sonnenschein, 1967) 通过对价格在市场经济中的实际运用情况进行分析发现, 在小型经济中, 任何超额需求函数的变化都不会改变其对应的价格。而在开放经济中, 国际价格的变动却会对社会福利产生影响, 其主要包括: (1) 有贸易时的福利水平好于没有贸易时; (2) 其他条件不变, 贸易条件的改善会提高潜在的福利水平; (3) 当只有两种固定商品供应时, 改善贸易条件或者存在高价格差带来的福利增加优于不改善贸易条件或者只存在低价格差。
在实际经验的基础上, 索南夏因对价格机制理论进行了不断探索。针对国际价格变动对社会福利的影响, 索南夏因等 (Foster & Sonnenschein, 1970) 从理论层面对国内价格变动影响社会福利的机制进行了研究。经济学家普遍认为, 政府征税或对某些行业补贴会导致经济扭曲。在一个扭曲的经济体系中, 仅仅改变单一的扭曲行为反而可能导致福利减少。索南夏因等运用包含N个商品的简单封闭经济模型, 检验了在何种条件下扭曲的径向减少 (radial decrease) 能够导致福利增加: (1) 当生产边际替代率不变且没有低质商品时, 经济中存在唯一均衡, 此时通过调整生产与消费之间的“税收楔子”能减少扭曲、增加社会福利。 (2) 当生产边界严格凹时, 经济中存在多重均衡。在存在多重均衡的经济体中, 特定均衡解的优化问题是困难的, 单纯地减税反而导致经济偏离最优状态。索南夏因等提出了三种调整机制:政府补贴、弹性工资调整制度和弹性价格调整机制。他们在解决价格扭曲问题的过程中进行了分类讨论, 从更深层次剖析了价格机制对社会福利的影响。这为之后价格公理化的提出奠定了理论基础, 也为政府管理者制定政策提供了理论框架。
通过对价格理论基础和实际经验的探索, 索南夏因 (Sonnenschein, 1974) 进一步研究了价格机制在资源配置中的作用。他将价格机制视为与竞争机制类似的资源配置机制, 通过研究如何为价格机制提供“绝对的” (categorical) 公理, 提出了价格机制的“识别” (identify) 机制: (1) 均衡存在; (2) 信息集中有唯一的价格信息; (3) 唯一价格信息是均衡价格; (4) 公理S。公理S指出, 给定任何被允许的信息和有限的经济体, 当扩大原始有限经济体构造出一个更大范围的有限经济体时, 此经济体的均衡信息集中包含了原始经济体中的信息。换句话说, 当经济体中增加了足够数量的其他消费者时, 有限个体会被淹没 (swamp) 。现有经济体中的均衡结果会被纳入更大范围的经济中, 构建均衡价格。因此当价格机制满足识别公理时, 存在从信息到价格的唯一映射, 使得每一种优化都是一个均衡。索南夏因对价格机制的公理化表示, 使我们在面临更多消费者或更大范围的经济时仍然能通过价格机制实现市场均衡。将价格机制描述为现实中的普遍目标, 表明了存在从隐性分配机制到价格机制的映射, 这使得通过价格机制反映消费者的实际选择过程成为以公理的方式表达完整社会选择过程的重要进步 (Plott, 1976) 。同时, 价格的识别公理也成了比较竞争性价格过程和其他过程的基本理论框架。
在对价格机制公理化的研究基础上, 索南夏因等对价格在消费者决策和厂商决策中的作用进行了理论探索。索南夏因等 (Novshek & Sonnenschein, 1979) 研究了消费者如何在不同品牌的商品中选择价格和质量特征。考虑一个可区分的商品模型, 价格诱导的需求变化可以分解为收入效用、替代效用和商品改变效用 (change-of-commodity effect) 。在价格发生变化时, 商品改变效用反映了消费者购买相似产品的比例, 这种效应总是负的。即使个人需求函数的斜率为正, 只要存在与价格变化的商品充分接近的可区分商品, 对商品改变效用的清晰认识也能保证市场对于该商品的需求函数的斜率为负。而在决定总需求函数的斜率时, 具有保留价格的边际消费者发挥了重要的作用。假设需求是由连续的消费者决定的, 此时价格的无穷小变化也会改变购买该商品的消费者数量。该框架在商品价格非连续变化的情形下同样适用。遗憾的是, 当时的总需求理论并未关注边际消费者, 也忽视了新古典收入, 这导致了替代效应的错误运用。索南夏因等对需求改变效用的分析, 一方面, 纠正了理论分析中的误区, 明确了边际消费者在需求理论中的重要作用。另一方面, 索南夏因等建立的需求模型也为用数据分析消费者行为提供了实用工具。随机扰动的各种概率分布衍生出了离散logit模型、广义logit模型和probit模型, 为经验性应用提供了相当大的灵活性。
价格变化改变社会资源配置, 一方面是通过价格信号诱导需求变化实现的, 另一方面是通过价格信号改变厂商进入决策、供给和利润实现的。是否存在足够的潜在利润引导经济向有效配置的方向发展是经济分析的一个经典话题。索南夏因 (Sonnenschein, 1981) 利用动态局部均衡模型, 探讨了当商品具有异质性时利润和价格作为厂商进入诱导因素对资源配置的影响。研究发现, 在市场向均衡状态进行调整的过程中, 市场中已有厂商会以与利润变化率成正比的速度向更高利润的方向调整商品生产, 以期实现厂商价值最大化。而市场外部厂商发现有利可图时, 也会进入市场改变市场中的供给与价格。此时, 需求与供给相等的均衡条件成为支配这种动态过程 (t?tonnement dynamics) 的手段, 从而厂商数量和商品价格随时间不断调整, 最终达到市场均衡价格和均衡数量。索南夏因利用供需相等的均衡条件探索市场价格和利润的调整机制, 发现在均衡利润为零的情况下, 资源可以达到有效配置。
综上所述, 在理论和实际两方面, 索南夏因对价格机制理论的拓展做出了重要贡献, 尤其是对价格机制公理化体系的建设。价格变化背后蕴含着消费者和厂商行为的改变, 对价格机制的公理化表达等价于以公理化方式完整表达社会选择过程, 使得该领域研究向前迈出了重要的一步。价格识别机制也成为区分价格机制与其他资源配置机制的重要标准之一。同时, 索南夏因等对消费者需求和厂商供给变化机理的讨论, 明晰了价格机制实现市场均衡的路径, 为之后学者研究价格机制及其作用奠定了坚实的基础。索南夏因也在该领域继续探索, 并将其运用到国际贸易领域中。雷布琴斯基定理 (Rybczynski theorem) 是国际贸易领域的重要定理之一。它关注商品生产和消费、要素价格和消费者财富是如何随要素禀赋的变化而变化的。索南夏因等 (Opp, Sonnenschein & Tombazos, 2009) 在赫克歇尔-俄林模型 (Heckscher-Ohlin model) 中对雷布琴斯基定理进行了重新探讨, 得出了相反的结论:一种生产要素禀赋的增加, 会导致密集使用该要素的商品生产的绝对减少和较少使用该要素的商品生产的绝对增加。这对当前国际贸易领域的实际运行发挥了重要的影响。
三、索南夏因对投票理论的贡献
阿罗在其所发表的《社会选择与个人价值》 (Arrow, 1951) 一书中提出了对任意一组个人偏好进行加总的机制。要使投票结果能够反映出大多数人的意见, 需要满足以下条件: (1) 社会价值观和个人价值观存在正向联系, 也称为弱帕累托原则 (weak Pareto principle) ——如果所有个体都认为某备选项 (alternative) 是最优的, 那么社会整体排序也认为该备选项最优。且当个体的价值观发生改变时, 相应的社会排序也会做出正向反应。 (2) 无关备选对象的独立性 (independence of irrelevant alternatives) ——每个人根据任意给定的集合做出的选择, 与不在该集合中的备选项无关。 (3) 公民主权 (citizens sovereignty) , 也称为无限制性 (unrestricted domain) ——每个人都能按照自己的价值观自由地选择备选项, 任何逻辑上可能的个人排序都不应该先验地被排除。 (4) 非独裁性 (non-dictatorship) ——社会选择不由某一个人的偏好决定。然而, 阿罗指出不存在一个同时满足这四项条件的社会福利函数, 这被称为“阿罗不可能定理” (Arrow's impossibility theorem) 。
图2 索南夏因对投票理论的贡献
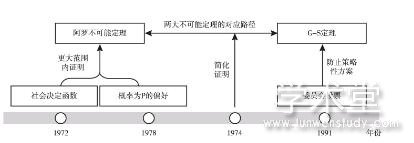
图2 索南夏因对投票理论的贡献 下载原图
从1972年起, 索南夏因等便开始关注投票理论的发展, 并通过对基本假设条件的弱化肯定了阿罗不可能定理在社会决定函数中的存在。阿罗关注是否存在同时满足四个条件且能够将任意个人偏好加总为社会偏好的机制。类似地, 森 (Sen, 1969) 研究是否存在某个规则能够将任意个人偏好集转变为能够在备选项中做出选择的组关系 (group relation) 。森将这种关系称为社会决定函数 (social decision function) 。社会决定函数加强了传递性假设, 森认为将传递性假设变为拟传递性 (quasi-transitive) 2假设能在不影响社会最优的前提下否定阿罗的不可能结果。然而, 索南夏因等 (Mas-Colell & Sonnenschein, 1972) 研究指出, 社会福利函数是满足传递性偏好关系的社会决定函数。通过引入正向响应 (positive responsiveness) 和弱独裁者 (weak dictator) 3概念, 索南夏因等重新肯定了阿罗不可能定理的作用。索南夏因等证明: (1) 具有拟传递偏好的社会决定函数, 不可能同时满足社会价值观和个人价值观存在正向联系、对无关备选对象的独立性和不存在弱独裁者 (或者正向响应) 三个基本条件。 (2) 当存在至少四个候选人时, 社会决定函数不可能同时满足社会价值观和个人价值观存在正向联系、对无关备选对象的独立性、不存在弱独裁者和正向响应四个条件。可见, 索南夏因等通过改变阿罗不可能定理的假设条件, 将该定理的讨论从特殊的社会福利函数拓展到一般的社会决定函数。他将森 (Sen, 1969) 对社会决定函数的研究方法引入到对阿罗不可能定理的研究中, 却得出了与森不同的结论, 即在偏好具有拟传递性的条件下, 阿罗不可能定理同样适用。
除了放松基本假设条件外, 索南夏因等进一步考虑了偏好彩票 (lottery) 的情况。阿罗对社会福利函数不可能性质的研究建立在将社会偏好域 (profiles) 转变为社会偏好关系的基础上。而索南夏因等 (Barbera & Sonnenschein, 1978) 扩大了阿罗不可能定理对偏好关系的研究范围, 考虑将社会偏好域转变为社会偏好关系上的彩票 (即社会福利组合, social welfare scheme) 。这在不改变个人偏好集合和维度的基础上, 增加了偏好加总可能产生的结果, 以及偏好加总产生令人满意的结果的可能性。在社会福利组合下“组织E能够保证偏好x甚于y”变为“组织E能够在概率P下保证偏好x甚于y”。这将讨论的社会偏好关系概率化, 从确定的1到概率P, 进而将社会偏好关系扩展为既包括原有的偏好关系, 也包括新增的以概率形式表示的社会偏好关系。阿罗不可能定理的适用范围得到极大扩展。
此后, 索南夏因等 (Schmeidler & Sonnenschein, 1974) 转向对防止策略性的研究, 并运用更简单的方式证明了吉伯德-萨特思韦特定理 (即G-S定理) , 明确了从阿罗不可能定理到G-S定理的对应路径。一方面为理解阿罗不可能定理提供了全新的视角, 另一方面也促进了G-S定理的不断发展。防止策略性是在策略性行为不能获益的假设下研究如何防止社会成员通过非真实表达个人偏好获得更高收益。如果至少有一个人在某种选择的情况下能够通过非真实投票获得不同于他真实偏好的结果, 那么该社会决定函数就是“可操作的” (manipulable) 。G-S定理指出, 社会决定函数无法同时满足防止策略性和不可操作两个要求。如果社会决定函数是防止策略性的, 同时有至少三个候选人时, 就存在独裁者。否则, 任何非独裁的社会决定函数都会是可操纵的。该结论在弱排序 (即允许无差异偏好) 的情况下同样成立。事实上, 许多投票方案被认为是可操作的。“维克里猜想” (Vickrey's conjecture) 指出, 为了避免投票过程中的非真实意愿表达, 决策程序需要满足特定的限制条件, 这些条件等价于阿罗不可能定理中的独立性和正向联系。然而, 阿罗不可能定理是不一致的。如果仅仅满足公民主权和非独裁者两个条件, 投票过程仍然是可操作的。Gibbard (1973) 对“维克里猜想”进行了证明:包含至少三个备选项的投票方案要么是可操作的, 要么是独裁的。然而, 他虽然基于阿罗不可能定理证明了上述结论, 但是“这并不是一个简单的方法”, 这在一定程度上增加了G-S定理被接受和使用的难度。而索南夏因通过简化从阿罗不可能定理到G-S定理的证明步骤, 使得G-S定理受到越来越多学者们的关注, 并催生了一系列的后续研究, 为G-S定理成为社会选择理论中最重要的结论之一添上了浓墨重彩的一笔。
在对G-S定理研究的基础上, 索南夏因等进一步探讨了如何解决不可操作问题。在存在N个投票者和K个备选项的条件下, 每个投票者对可能采取的2K个子集进行线性排序。投票方案则将投票者的线性排序转变为目标集合。G-S定理指出, 如果存在多个目标, 所有不可操作的投票方案都是独裁的。克拉克 (Clarke, 1971) 提出了税收激励机制:将达成投票目标所获得的收益与需要付出的成本分离, 以促使投票者真实表达自己的偏好。该机制解决了“搭便车”问题, 并且满足不可操作性。索南夏因等 (Barbera, Sonnenschein & Zhou, 1991) 借鉴该机制提出了“委员会投票” (voting by committees) 概念作为偏好域中不可操作方案的唯一形式, 这也是防止策略性操作的社会决定函数的形式。委员会投票需要满足以下性质: (1) 在考虑N维空间 (hypercube) 4的情况下, 单峰偏好 (single-peaked) 是可分离的, 委员会投票在可分离偏好 (separable preferences) 领域是防止策略性的5。 (2) 中位数空间 (median spaces) 6在防止策略性中发挥了重要的作用。 (3) 需要满足选民主权 (voter sovereignty) 、中位性 (neutral) 和匿名性 (anonymous) 7的要求。索南夏因等“委员会投票”概念的提出明确了不可操作方案应该具有何种性质, 将防止策略性研究向前推进了一大步。
综上所述, 索南夏因等通过对社会决定函数施加限制以及对概率为P的偏好的引入, 在更大范围内推广了阿罗不可能定理, 促进了学者从更深层次研究阿罗不可能定理。1977年, 森又通过对社会决定函数一致性 (consistency) 与二元偏好规则性 (regularity) 间响应的探索, 重新解释了阿罗不可能结果。经过反复的探讨与研究, 阿罗不可能定理不断发展, 而森也部分因为解决了“投票悖论”获得了1998年诺贝尔经济学奖, 在此过程中索南夏因的贡献不可忽视。阿罗不可能定理表明, 在偏好已知的情况下, 不存在将个人偏好加总为社会偏好的机制;而G-S定理则表明, 不存在让社会成员真实表达自身偏好的机制。虽然二者讨论的不可能问题的重点不同, 但索南夏因等的简化证明使更多学者意识到G-S定理和阿罗不可能定理的关系, 两大不可能理论的共同作用给政治经济学的发展提出了新的挑战。之后, 学者们从改变简单多数规则入手, 例如委员会投票、议程设置模型等的讨论, 带来了政治经济学新一轮的发展。
四、索南夏因对非合作谈判理论的贡献
20世纪70年代, 学术界对讨价还价 (bargaining) 问题展开了广泛的讨论, 越来越多的学者开始基于非合作博弈视角研究讨价还价问题。通过博弈论方法, 可以对盈余分配方式进行准确的预测, 从而解决之前困扰学术界的谈判问题。鲁宾斯坦 (Rubinstein, 1982) 认为讨价还价模型是一个完美的子博弈纳什均衡, 交替报价的谈判制度使最终谈判收益的划分取决于代理人的时间偏好、报价的时间间隔以及哪个参与者优先采取行动。当双方报价之间的时间间隔趋近于零时, 博弈中的先发优势将会消失, 最终的收益划分将趋近于均等分配。该结论在学术界引起了强烈的反响。在此之前, 经济学家普遍认为纯粹的双寡头垄断问题的结果应该是不确定的, 但是鲁宾斯坦这种简单的分析框架却得出了令人信服的结论。
索南夏因等 (Gul, Sonnenschein & Wilson, 1986) 将讨价还价模型应用于垄断分析中, 对“科斯猜想” (Coase conjecture) 8进行了检验。他们还将卖方对多个消费者进行重复交替报价的情境引入到讨价还价模型, 扩展了鲁宾斯坦对于双边寡头谈判问题的分析。在动态垄断情境中, 垄断者不会在第一时间给出最低的报价, 消费者也很容易意识到这一点。因此, 在厂商第一次报价时, 消费者可以选择不进行购买, 等待之后的报价。基于此, 可以将垄断者定价问题视为“讨价还价”模型。鲁宾斯坦认为在双边寡头定价问题中, 会存在唯一的子博弈完美均衡的纯策略, 贴现率的引入能够确定最终的贸易利益分配。但是索南夏因等的研究发现, 当垄断者对具有连续偏好的消费者报价时, 实际情境比鲁宾斯坦模型的分析更为复杂。在垄断者报价的每个时期里, 市场上都存在子博弈纳什均衡。当市场满足零成本、正利率且买方偏好具有连续性等假设时, 如果买方对于商品估值是正的, 那么存在唯一均衡且买方策略固定, 均衡价格沿着均衡路径变动。因此“科斯猜想”被证明是一个固定的策略:缩短报价周期的长度, 将会使价格降至零或者最小值。
索南夏因等 (Neelin, Sonnenschein & Spiegel, 1988) 还通过设计经济实验, 对鲁宾斯坦提出的讨价还价模型进行再检验, 讨论当谈判延长至两个回合以上时逆向归纳法求解的均衡结果是否稳定。在实验设计的“讨价还价”环节中, 由一方决定如何划分“馅饼”, 另一方决定接受或者拒绝。如果选择接受, 则整个博弈结束;如果选择拒绝, 那么博弈将进入下一轮, 此时玩家之间交换权力。“馅饼”的价值在每一轮都会缩水, 如果双方在规定的回合里未达成协议, 那么双方将不获得任何回报。实验分为两个、三个、五个回合三种情境, 研究结果发现, 在博弈回合为两个回合时, 实验结果与鲁宾斯坦讨价还价模型完全相同, 最终财富分配也符合逆向归纳法所得出的结果。但是在多回合的博弈中, 实验结果与理论预测出现偏离, 且不随实验者经验和利害关系变化而发生改变。尤其是在多于三个回合后, 这种偏离最为明显, 甚至在部分实验中, 参与双方同意平均分配财富份额。
除了对已有理论进行经济实验检验, 索南夏因等 (Gul & Sonnenschein, 1988) 还讨论了“单边不确定性谈判”中的延迟问题。他们认为, 在鲁宾斯坦的讨价还价模型中, 均衡的唯一性导致买方肯定会接受卖方第一轮的报价。但是在实际情境中, 交易不可能毫无延迟地发生。为了体现这种延迟性, 索南夏因等在博弈模型中引入不完全信息是具有说服力的。假设卖方的估值和买方的类型 (type) 分布是共同知识, 但是买方的真实类型是私人信息。在信息不完全的谈判过程中, 参与者通过报价中花费的时间来显示他们的估值, 最终的博弈结果只有在一些延迟之后才会产生。索南夏因等的研究将完全信息下的鲁宾斯坦讨价还价模型推广至不完全信息情境中, 并对纯策略下的序贯均衡进行适当改进。通过推演发现, 在不完全信息情境中, 当满足策略连续性和信念稳定性与单调性假设时, 能得到唯一的均衡策略, 所有类型的买方都会以大致相同的价格进行报价交易。该结论背后的逻辑是, 虽然估值不同的买方在不同时间会支付不同的价格, 但是当报价之间的时间间隔很小时, 短时间内会给出大量可供筛选的报价。如果不同类型的买方报价接近同一水平, 那么剩余的买方不会表现出差异态度, 并会更快给出其报价。因此, 当报价之间间隔时间很短时, 讨价还价博弈会快速发生。
综上所述, 索南夏因等在对鲁宾斯坦讨价还价模型的研究基础上, 不仅设计博弈实验在多个回合中检验了逆向归纳法的适用性, 还进一步地扩展了鲁宾斯坦对双边寡头谈判问题的分析, 并将讨价还价模型从完美信息推演至具有“单边不确定性”的不完美信息情境中。索南夏因等的研究具有很强的启发与引导作用, 使得对于“双边不确定性”情境的讨论成为可能, 而不完全信息的引入为“柠檬市场”问题的进一步研究打下了理论与模型的基础。
五、总结与评论
索南夏因在微观经济学理论的发展中具有举足轻重的地位, 他与合作者在一般均衡理论、价格机制研究、投票理论和非合作谈判理论上都做出了重要的贡献, 极大地推动了上述领域的研究进展。不仅如此, 索南夏因在竞争性一般均衡、古诺寡头模型、激励相容、机制设计、空间经济的均衡等问题上也颇有建树, 其对微观经济学的研究既有理论深度, 又有领域宽度。
首先, 根据索南夏因、曼特尔、德布鲁的研究所总结出的索南夏因-曼特尔-德布鲁定理, 是一般均衡理论发展历史上极其重要的定理。该定理表明, 除了需要满足连续性、零次齐次性和瓦尔拉斯法则外, 个人超额需求函数的其他属性并未体现在总超额需求函数中。这切断了个人需求函数和总超额需求函数的联系, 使得微观经济学中对个人消费行为的理性假设与宏观总超额需求函数不存在相同的落脚点, 这导致了微观基础和宏观理论的分离。同时, 超额需求函数是研究一般均衡理论的重要途径, 索南夏因-曼特尔-德布鲁定理对总超额需求函数不唯一性的证明, 直接反映了经济中均衡点的不唯一性, 并确认了不稳定性。该定理实质上揭示了一般均衡理论的不可证伪性, 直接影响其后续的发展。第二, 索南夏因对价格机制公理化表达的开创性研究, 成为区分竞争性价格过程与其他资源配置过程的理论框架, 使得社会选择过程向公理化方向发展迈出了重要的一步。不仅如此, 索南夏因等运用价格机制对消费者的需求变动和厂商的供给变动的内在逻辑进行解释, 也对国际贸易领域要素禀赋和价格机制的作用进行了分析, 完善了其对价格机制的研究。第三, 索南夏因等在社会决定函数和偏好彩票领域推广了阿罗不可能定理, 在更大范围内肯定了阿罗不可能定理。而其从阿罗不可能定理到G-S定理证明路径的简化, 展示了两大不可能定理的对应路径, 共同推动了政治经济学的发展, 也奠定了G-S定理在社会选择理论中的地位。同时, 委员会投票概念的提出则成为防止策略性研究中的重要突破, 促进了投票理论的发展。第四, 索南夏因在对鲁宾斯坦讨价还价模型的研究基础上, 检验了该模型在多回合博弈中实际结果与理论预测的差异, 并更进一步地引入卖方对于多个消费者进行重复交替报价的情境和具有“单边不确定性”的不完美信息情境, 扩展了鲁宾斯坦对双边寡头谈判问题的分析。索南夏因在上述领域的研究体现出其深厚的理论洞察力和成熟的建模分析经验, 取得的诸多具有启发性的成果对经济学发展具有重要的理论和现实意义。
参考文献
[]Arrow, K.J. & G.Debreu (1954) , “Existence of an equilibrium for a competitive economy”, Econometrica 22 (3) :265-290.
[]Anderson, R.M. & H.Sonnenschein (1982) , “On the existence of rational expectations equilibrium”, Journal of Economic Theory 26 (2) :261-278.
[]Anderson, R.M. & H.Sonnenschein (1985) , “Rational expectations equilibrium with econometric models”, Review of Economic Studies 52 (3) :359-369.
[]Barbera, S. & H.Sonnenschein (1978) , “Preference aggregation with randomized social orderings”, Journal of Economic Theory 18 (2) :244-254.
[]Barbera, S., H.Sonnenschein & L.Zhou (1991) , “Voting by committees”, Econometrica 59 (3) :595-609.
[]Brown, D.J. & R.L.Matzkin (1996) , “Testable restrictions on the equilibrium manifold”, Econometrica 64 (6) :1249-1262.
[]Carvajal, A. et al (2004) , “Equilibrium behavior in markets and games: Testable restrictions and identification”, Journal of Mathematical Economics 40 (1-2) :1-40.
[]Cheng, J.Q. & M.P.Wellman (1998) , “The Walras algorithm: A convergent distributed implementation of general equilibrium outcomes”, Computational Economics 12 (1) :1-24.
[]Chiappori, P.A. & I.Ekeland (2004) , “Individual excess demands”, Journal of Mathematical Economics 40 (1) :41-57.
[]Clarke, E.H. (1971) , “Multipart pricing of public goods”, Public Choice 11 (1) :17-33.
[]Debreu, G. (1974) , “Excess demand functions”, Journal of Mathematical Economics 1 (1) :15-21.
[]Foster, E. & H.Sonnenschein (1970) , “Price distortion and economic welfare”, Econometrica 38 (2) :281-297.
[]Gibbard, A. (1973) , “Manipulation of voting schemes: A general result”, Econometrica 41 (4) :587-601.
[]Gul, F. & H.Sonnenschein (1988) , “On delay in bargaining with one-sided uncertainty”, Econometrica 56 (3) :601-611.
[]Gul, F., H.Sonnenschein & R.Wilson (1986) , “Foundations of dynamic monopoly and the Coase conjecture”, Journal of Economic Theory 39 (1) :155-190.
[]Hahn, F.H. (1975) , “Revival of political economy: The wrong issues and the wrong argument”, Economic Record 51 (3) :360-364.
[]Hands, D.W. (2012) , “The rise and fall of Walrasian microeconomics: The Keynesian effect”, In: P.G.Duarte & G.T.Lima (eds) , Microfoundations Reconsidered: The Relationship of Micro and Macroeconomics in Historical Perspective, Edward Elgar.
[]Ingrao, B. & G.Israel (1990) , The Invisible Hand: Economic Equilibrium in the History of Science, Cambridge University Press.
[]Kehoe, T.J. (1985) , “Multiplicity of equilibria and comparative statics”, Quarterly Journal of Economics 100 (1) :119-147.
[]Kirman, A. (1989) , “The intrinsic limits of modern economic theory: The emperor has no clothes”, Economic Journal 99 (395) :126-139.
[]Krueger, A.O. & H.Sonnenschein (1967) , “The terms of trade, the gains from trade and price divergence”, International Economic Review 8 (1) :121-127.
[]Mantel, R.R. (1974) , “On the characterization of aggregate excess demand”, Journal of Economic Theory 7 (3) :348-353.
[]Mas-Colell, A. & H.Sonnenschein (1972) , “General possibility theorems for group decisions”, Review of Economic Studies 39 (2) :185-192.
[]Mas-Colell, A. et al (1995) , Microeconomic Theory, Oxford University Press.
[]Neelin, J., H.Sonnenschein & M.Spiegel (1988) , “A further test of noncooperative bargaining theory: Comment”, American Economic Review 78 (4) :824-836.
[]Novshek, W. & H.Sonnenschein (1979) , “Marginal consumers and neoclassical demand theory”, Journal of Political Economy 87 (6) :1368-1376.
[]Opp, M.M., H.Sonnenschein & C.G.Tombazos (2009) , “Rybczynski's theorem in the Heckscher-Ohlin world— Anything goes”, Journal of International Economics 79 (1) :137-142.
[]Plott, C.R. (1976) , “Axiomatic social choice theory: An overview and interpretation”, American Journal of Political Science 20 (3) :511-596.
[]Rubinstein, A. (1982) , “Perfect equilibrium in a bargaining model”, Econometrica 50 (1) :97-109.
[]Samuelson, P.A. (1941) , “The stability of equilibrium: Comparative statics and dynamics”, Econometrica 9 (2) :97-120.
[]Schmeidler, D. & H. Sonnenschein (1974) , “The possibility of a cheat proof social choice function: A theorem of A. Gibbard and M. Satterthwaite”, Discussion Paper No.89, The Center for Mathematical Studies in Economics and Management Science, Northwestern University, Evanston.
[]Sen, A. (1969) , “Quasi-transitivity, rational choice and collective decisions”, Review of Economic Studies 36 (107) :381-393.
[]Shafer, W. & H.Sonnenschein (1982) , “Market demand and excess demand functions”, in: K.J.Arrow & M.D. Intriligator (eds) , Handbook of Mathematical Economics, vol.2, Elsevier.
[]Sonnenschein, H. (1972) , “Market excess demand functions”, Econometrica 40 (3) :549-563.
[]Sonnenschein, H. (1973) , “Do Walras' identity and continuity characterize the class of community excess demand functions?”, Journal of Economic Theory 6 (4) :345-354.
[]Sonnenschein, H. (1974) , “An axiomatic characterization of the price mechanism”, Econometrica 42 (3) :425-433.
[]Sonnenschein, H. (1981) , “Price dynamics and the disappearance of short-run profits: An example”, Journal of Mathematical Economics 8 (2) :201-204.
[]Sonnenschein, H. (2017) , “Chicago and the origins of modern general equilibrium”, Journal of Political Economy 125 (6) :1728-1736.
[]Tohme, F. (2006) , “Rolf Mantel and the computability of general equilibria: On the origins of the Sonnenschein-Mantel-Debreu theorem”, History of Political Economy 38 (1) :213-227.
[]Walras, L. (1874) , Elements d'economie politique pure, lausanne: L.Corbaz. Transl. By William Jaffe as Elements of Pure Economics, Homewood, III.: Richard D.Irwin, 1954.
注释
1 均衡流形是一组禀赋和价格的有序对集合, 对于给定的效用函数集, 市场超额需求函数为零。考虑到比较静态的逻辑, 均衡流形是用来研究一般均衡的可检验限制的适当选择:即允许作为系统外生变量的个体禀赋变化, 从而导出对系统内生变量均衡价格的限制。
2 拟传递性是指, xPy且yPz, 则xPz。而传递性包含两部分:一是xPy且yPz, 则xPz;二是xPy且yIz, 则xPz。
3 正向响应要求社会判断在个人判断上具有很强的单调性。弱独裁者是指, 对任何x和y, 个人偏好x甚于y能保证社会不会偏好y甚于x。
4 N维空间:当存在N个投票者和K个备选项时, 每个投票者对可能采取的2K个子集进行线性排序, 令P表示在2K上的所有排序, 对于此类顺序的每个N维组合产生一个集合。那么, 一个投票组合f是从pN到2K的函数。
5 单峰偏好:在一组备选项中, 选民有一个最偏好的选择。从最偏好选择向其他任何备选项的偏离都会导致效用降低。可分离偏好:称选民的偏好是可分离的, 意味着对于备选项集合S, 加入一个“好”的备选项比原来集合更好, 加入“坏”的备选项比原来集合更坏。
6 中位数空间:对于所有x, y, z∈X, 存在m=m (x, y, z) ∈X, 被称为x, y, z的中位数。其中, m在任何{x, y, z}组合的中间, 例如{ (x, m, y) , (x, m, z) , (y, m, z) }。即不论x, y和z间如何进行组合, 处于中间位置的个体就是该组合的中位数。
7 选民主权是指不能预先禁止某一种选举结果的产生 (选民可以表达对任何候选人的支持) 。中位性是指选举对象不会因其“名字” (name) 等因素而受到青睐。匿名性是指保证每个选民享受同等待遇, 保证“一人一票”的需要。
8 “科斯猜想”指出, 由于将来销售的耐用品将会影响到现在所售出的产品的未来价值, 在垄断耐用品生产者没有对未来的产量水平做出承诺时, 如果消费者具有价格下跌的理性预期, 那么垄断价格就会迅速降到边际成本水平。





