
1 前言
我国开展混凝土耐久性的研究较早,七五期间,我国就开展了混凝土耐久性的系统研究,取得了一定成果。九五期间,我国开展了混凝土耐久性广泛的研究,在《混凝土结构设计规范》GB50010-2001 修编时,引入了相关的章节。十一五期间,是我国混凝土耐久性研究成果最多的时期,修编出版了《普通混凝土长期性能和耐久性能试验方法标准》GB/T50082-2009,编制了《混凝土结构耐久性设计规范》GB/T50476-2008,《混凝土结构耐久性评定标准》CECS220:2007,《混凝土耐久性检验评定标准》JGJ/T193-2009。
混凝土碳化破坏的影响因素较多,我国混凝土耐久性规范对混凝土均采用“双控”的要求,控制最低混凝土强度等级,控制最大水胶比和最小水泥用量,显然混凝土的抗碳化能力是碳化破坏的主要因素。混凝土的碳化系数是反映其抗碳化能力的主要指标,混凝土的碳化系数与硬化混凝土的力学指标立方体抗压强度 有密切关系,德国在 1967 年提出的“Smolezyk 模型”是较早描述这一关系的数学模型,由于硬化混凝土的碳化系数与混凝土的强度相关性很好,建立塑性混凝土的主要指标孔隙比、水泥用量与强度的关系,就可建立与碳化系数的关系,笔者根据国内奈系混凝土的使用情况研究了混凝土强度与混凝土碳化系数的关系,本文对在一研究的情况做一介绍,希望能达到“抛砖引玉”的作用。
2 混凝土碳化的本构关系
2.1 混凝土的孔结构和微观裂缝
混凝土的强度、渗透性和抗碳化性能取决于混凝土的孔结构,孔结构可分为凝胶孔和毛细孔。凝胶孔对混凝土无害,而毛细孔的最可几孔径(出现几率最大的孔径)分布对混凝土的强度和抗渗性有比较大的影响,混凝土内部连通的孔隙和毛细孔通道,则是造成抗渗性降低的主要原因。
美国加州大学的 MehtaPK 的试验表明:孔径小于 1320? 孔对混凝土的抗渗性和强度将不产生影响。Metha 将孔隙按孔径直径 d 分为 4 个等级:d<20nm(1nm=10?)的无害孔;d 为 20~50nm 少害孔;d 为50~100nm 的有害孔;d>100nm 的多害孔。
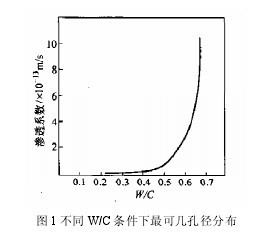
混凝土毛细孔则因水胶比和水化程度的差异,孔径变化较大,可分为少害孔、有害孔和多害孔。混凝土凝结时,随水胶比减小时,混凝土的总孔隙率减小,胶凝孔含量增多,毛细孔则减少。减水剂是提高混凝土的抗碳化能力的最主要的因素,水胶比不同,水泥水化的晶体结构、孔结构、微观裂缝及水化程度均发生明显差异。当水胶比小于 0.5 时,随水胶比的变化混凝土的最可几孔径分布明显向少害孔移动,毛细孔迅速减少,混凝土的渗透性也迅速减小(图 1)。当水胶比大于 0.5 后,混凝土的抗渗性能迅速降低。混凝土的水胶比也影响着浆料与骨料的边界厚度,当水胶比为 0.6 时,浆料与骨料的边界厚度约为 30um,容易形成粗大晶体和较多大孔,较大水胶比混凝土的多余水分蒸发和泌水是造成混凝土内部孔隙连通和产生毛细孔的重要原因。当水胶比为 0.4 时,浆料与骨料的边界厚度猛降到 5um,形成较小的晶体和较少的大孔,使混凝土的抗碳化能力提高。当水胶比大于 0.42 时,水泥的水化程度达到100%。水泥水化时水化热的降温梯度是在塑性混凝土中产生微观裂缝的主要原因。根据哈尔滨工业大学的试验结果分析,当混凝土的水胶比小于 0.36 时,混凝土的早期自收缩会异常加大,在约束条件下混凝土的微观裂缝会增多,其抗渗能力和抗碳化性能也相对降低。【图1】
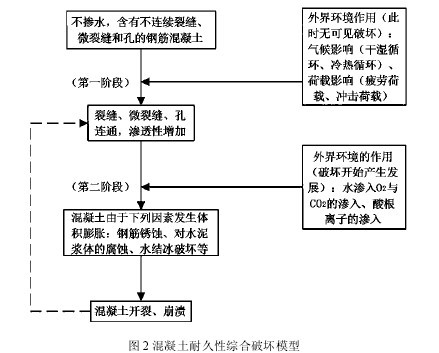
1994 年,美国 P.K.Mehta 提出了混凝土耐久性综合破坏模型。【图2】
2.2 国内减水剂的使用情况
笔者按国内减水剂的使用情况将“普通混凝土”划为三代,以便对混凝土的碳化本构关系进行描述,也有助于试验数据的收集整理和分类统计,以下简称为“第一代混凝土”,“第二代混凝土”,“第三代混凝土”。第一代混凝土:约 1990 年前,木钙类减水剂(不掺或少掺)水灰比在 0.5~0.6,一般没有掺合料,一般为 30~50mm,水调整,非泵送,水用量大,耐久性一般。第二代混凝土:约 1990 年后,奈系类减水剂,减水性能好,水胶比可控制在 0.45 左右,掺合料为粉煤灰(掺或不掺),坍落度在 180mm 左右,泵送,大量减少水用量,耐久性较好。第三代混凝土:约 2000 年后,聚羧酸类减水剂(主要用于中高强高性能混凝土),水胶比可控制在 0.4 左右,掺合料为粉煤灰、磨细矿粉、硅粉,坍落度在 180mm 左右,泵送,减水性能更好,水用量更少,耐久性更好。近年来聚羧酸类减水剂也用于中低强度混凝土。
2001 年为研究混凝土的早期开裂原因,中国建筑科学研究院组织国内 14 个研究单位开展了相关研究,并对国内奈系混凝土的使用情况进行了调查,调查情况如表 1 所示。【表1】

表格中,笔者增加了一个混凝土“浆体积比”的统计参数,此概念由普通混凝土配合比试验时“控制浆骨体积比”的概念转换而来,一般要求塑性混凝土的浆骨体积比为 0.35:0.65 以下,水泥浆体积比控制在 0.27~0.35,相同强度等级的混凝土浆体积比提高一些,混凝土的早期强度高一些,但混凝土 28d 的强度相应低一些。浆骨体积比小于 0.27 的混凝土则为干硬性混凝土,浇筑时采用平板振捣器或碾压成型。浆骨体积比大于 0.35 的高强混凝土,由于采用高活性的硅灰等掺合料,混凝土的孔结构分布、水化热和水化过程已与普通混凝土不同,其抗渗性能和抗碳化性能总体较高。
3 混凝土碳化数学模型的分析与研究
混凝土碳化的影响因素较多,有外部因素和内部因素。外部作用因素包括:CO2浓度、湿度、温度、应力、位置等。内部影响因素包括:用水量及水胶比、水泥用量及水泥品种、减水剂品种、掺合料品种、粗骨料及骨料的级配,拌合、浇筑振捣、养护等。
在笔者收集到的混凝土碳化深度预估模型有 18 个,(1)日本 Nishi、浜田岸谷学者碳化模型(1962、1963),(2)日本规范模型,(3)德国 Smolczyk 模型(1967),(4)中建院的多系数碳化模型(1982),(5)Tuutti 碳化模型(1982),(6)龚洛书模型(1985),(7)山东朱安民碳化模型(1985),(8)西安张令茂(1990),(8)上海黄士元碳化模型(1991),(10)希腊 Papadakis 碳化模型(1991,2000),(11)邸小坛两个碳化模型(1994),(12)Lesahe de contenay 模型(1995),(13)张誉模型(1996),(14)上海刘亚芹(1997),(15)牛荻涛碳化预测随机模型(1999),(16)CEB TG V,1+2碳化模型(2000),(17)南京吴绍章模型(2000),(18)张海燕模型(2006)。18 种碳化深度数学模型基本上反映混凝土碳化的影响因素。
碳化深度数学模型基本可分为以下几个类型:(1)基于扩散理论,有张誉模型、刘亚芹模型;(2)基于物理-化学反应,有 Tuutti 模型、希腊 Papadakis 模型、CEB TG V,1 + 2 模型;(3)基于实验室的多系数模型,塑性混凝土碳化数学模型自变量为 W/C 或 W/C+C。(4)其他的为基于工程观察的多系数模型,硬化混凝土碳化数学模型自变量为 。笔者根据混凝土碳化的本构关系对这些数学模型的主要自变量进行了初步研究。
3.1 碳化系数 K 与塑性混凝土 W/C,C 的关系
多数混凝土碳化数学模型将塑性混凝土的水胶比作为碳化数学模型的第一自变量,这与水胶比对硬化混凝土的孔结构的影响有关(图 1):当混凝土的水胶比大于 0.5 时,混凝土的有害孔隙明显增多,混凝土的抗渗能力大大下降,即混凝土的抗碳化能力明显下降。笔者认为:对水胶比大于 0.5 的混凝土,水胶比作为碳化数学模型的“单自变量”,能较好反映混凝土的碳化情况混凝土。对水胶比小于 0.5 的混凝土,水胶比作为碳化数学模型的单一自变量,则不能反映混凝土的碳化情况,从表 99 可知,采用奈系高效减水剂的混凝土抗压等级从 C20 上升到 C50,混凝土的用水量只从 190Kg 降到 182Kg,水的用量变化很小,强度等级提高基本只与胶凝材料的用量有主要关系,因此,应当用有水泥用量的“双自变量模型”或“多自变量模型”来描述塑性混凝土碳化的本构关系。
3.2 碳化系数 K 与硬化混凝土抗压强度 的关系
德国“Smolezyk 数学模型”计算的碳化系数 K 与 的关系曲线与“CECS220 数学模型”计算的 K与 的数学模型表达的关系是一致的。
德国“Smolezyk 数学模型”给了一个极限混凝土强度的概念,认为 时,K=0.笔者认为“Smolezyk 数学模型”的极限混凝土强度的概念只是一个数学概念,而不是一个物理概念。不管混凝土自身强度多高,只要混凝土存在“孔、隙”就有渗透性,就存在碳化的可能,只有 K 值较小而已。混凝土自身的抗碳化能力有一个极限,根据哈尔滨工业大学的试验结果,当混凝土的水胶比小于 0.36时,混凝土早期自收缩会异常加大,在约束条件下混凝土的微观裂缝会增多,由于抗渗能力降低,混凝土的抗碳化性能也会相对降低,而不是“趋于零”。对抗碳化要求更高的混凝土结构则要采取防腐措施,如在混凝土表面涂丙烯酸防碳化涂层。
4“胡苏模型”的建立与验证
在笔者收集的十八种混凝土碳化深度数学模型中,同济大学的“张誉模型”是基于 Fick 第一定律最好的数学解析模型,但其不适用于“低湿度”条件。在分析“张誉模型”的这个问题时,发现是在引用希腊学者 Papadakisde 有效扩散系数 De时造成的。
张海燕模型提供了不同湿度条件下的快速碳化湿度模型,当湿度从 40%增大到 80%时,碳化深度逐步减小,但笔者认为该湿度模型也不准确,CECS220:2007 提供了一个偏峰的最大二乘法模型,其最大峰值对应的湿度为 60%,牛荻涛湿度模型的最大峰值对应的湿度为 50%,Papadakisde 的试验结果(表2)表明,相同条件下,湿度 45%、55%的碳化深度比湿度 35%、70%的碳化深度大 3-4mm,这符合湿度对混凝土碳化影响的本构关系,即湿度为 0%时没有电解液,不会发生碳化化学反应,湿度为 100%时,CO2气体基本无法渗入,碳化化学反应极慢。【表2】
在对比几种湿度模型的关系后,笔者采用“略偏峰的微瘦的”一元二次方程湿度模型(图 3)对“张誉模型”简单修改,很轻易的解决了“张誉模型”不适用于“低湿度”条件的问题。【图3】

修改后的碳化深度数学模型如下:【5】

笔者将这一混凝土碳化数学模型称为“胡苏配合比模型”。与 Papadakis 的试验结果的误差见表 2,其绝对误差为 1.1mm,相对误差小于 5%,验算结果与试验结果基本一致。
Papadakis 的碳化试验是在试块 90d 水养护条件下进行的,混凝土的水化程度高,避免了混凝土早期复杂反应的过程带来的误差,即使 5d 的碳化也能反映混凝土的碳化本构关系。因此,笔者建议:(1)碳化试验应在混凝土“水养护”90d 充分水化进行,(2)现在的快速碳化试验箱应加装“自动湿度调控仪器系统”,用不同湿度的快速碳化试验结果建立更好。的碳化湿度模型,(3)碳化试验采用 40%~60%的 CO2体积浓度,碳化时间为 5d~10d 的试验时间进行。建议快速碳化试验开展这一方面的研究从表 2 可得混凝土强度等级与与水胶比和水泥用量有很好的直线数学函数关系。笔者又根据“胡苏配合比模型”计算结果进行了一次的转换,提出以下混凝土碳化系数数学模型,该模型适用于奈系混凝土:【6】

笔者将这一混凝土碳化数学模型称为“胡苏抗压强度模型”。经计算,第二代混凝土的近视极限值为 65MPa,这与基于试验观察“邸小坛模型”提出的 60MPa基本一致。
从图 4 可见,“胡苏抗压强度模型”在最不利湿度(RH=52%)条件下计算的碳化系数处于“Smolezyk数学模型”与“CECS220 思想模型”的计算结果之间,在 C35 以上时与“Smolezyk 模型”接近,显然“Smolezyk 碳化系数模型”是试验室快速碳化的最不利结果。“胡苏抗压强度模型”数学模型简单,基本反映了混凝土抗压强度与抗碳化能力的关系。但笔者认为:由于混凝土强度还与混凝土的“浆骨比”有关,其也不能完全反映混凝土的抗碳化能力,对暴露混凝土工程进行碳化破坏评估时,应结合混凝土的实际碳化情况综合分析。
5 结论与建议
1.混凝土碳化的影响因素较多,有外部因素和内部因素。混凝土的碳化速率取决于混凝土的孔隙结果和微观裂缝,其碳化速度是由孔隙中二氧化碳的化学反应和和微观裂缝的渗透性综合决定的。
2.本文提出的“胡苏模型”有一定的实用价值,尚需进一步的数学推导和工程验证。碳化深度的数学模型建立时,外因应以湿度为第一自变量,内因应以水胶比为第一自变量,混凝土碳化深度数学模型应采用多参数的综合模型。
3.现有的快速碳化试验方法与现代混凝土的本构关系不适应,建议快速碳化试验在胶凝材料充分水化后、在混凝土试块标养 90d 后进行,快速碳化试验应设置精确的“湿度自动调控系统”,湿度控制由70%降到最不利湿度 50%左右。在快速碳化试验时,应“增加一组”同条件立方体试块在快速碳化试验结束后进行混凝土抗压强度试验,以便检查快速碳化试验的碳化系数变化和误差情况。
参考文献:
[1]P.K Mehta. Concrete Technology at the Crossroads--Problems and Opportunities. Concrete Technology –Past, Present and future,proceeding of V. M. Malhotra Symposium [J]. ACI SP144,1994
[2] 高小建, 巴恒静, 祁景玉. 混凝土水灰比与其早期收缩特性关系的研究[C]. 化学工业出版社, 2004:86-93.
[3] 郭剑飞, 影响混凝土耐久性的微观因素--孔结构的理论分析[C].北京: 机械工业出版社, 2006:259-266.
[4] 何星华, 高小旺, 何淑君. 建筑工程裂缝防治指南[M]. 中国建筑工业出版社, 2005 :129-135.
[5] 李浩, 施养杭. 混凝土碳化深度预测模型的比对与分析[J]. 工业建筑, 2007, 28(2):192-195.
[6] 姚燕. 新型混凝土耐久性的研究与工程应用[M]. 北京:中国建材工业出版社, 2004 :438-443,592-594,599-614.
[7] 张誉, 蒋利学. 基于碳化机理的混凝土碳化深度实用数学模型[J]. 工业建筑, 1998, 28(1):16-19,47.
[8]张海燕,把多铎,王正中.混凝土碳化深度的预测模型[J]. 武汉大学学报, 2006,39(5):42-45.
[9] 牛荻涛, 董振平, 浦聿修. 预测混凝土碳化深度的随机模型[J]. 工业建筑, 1999, 29(9):41-45.
[10]邸小坛, 周燕. 混凝土碳化规律研究[R]. 北京:中国建筑科学研究院结构所, 1994.





