物理常数是物理学重要的组成部分，在物理学中占有特殊的地位，“各种物理现象以各种不同的方式联系到有关的一些物理常数。”物理常数在物理学中的重要性，也受到一些哲学家的关注，罗素认为：“基本物理常数的发现和测量是现代物理学最坚实的成就。”
随着现代物理学的发展，物理常数的存因问题越来越受到物理学家的重视，为此像爱丁顿等一些前辈物理学家不惜拆诸“数字学”，期望从中能发现解释物理常数的端倪，现代一批天才的物理学家想用弦/M 理论构建的统一理论，一揽子解决物理常数的解释问题。虽然这些工作对解释物理常数不无启发，但均没有获得显著的进展。因此，有必要做些哲学上的思考，以厘清对物理常数的认识与解释上存在的问题。
1、 关于物理常数
对什么是物理常数，大多数情况下人们认同恩格斯对物理常数所做的定义，即“物理学的所谓常数，大部分不外是这样一些关节点的标记，在这些关节点上，运动的量的（变化）增加或减少会引起该物体状态的质的变化，所以在这些关节点上，量转化为质。”实际上恩格斯在这里只是对当时已认识的物理常数做的一点哲学概括，以阐明哲学的“量变质变规律”，这也是之后一些对物理常数做哲学思考的方法。其实不要说恩格斯在这段话中只说了“大部分”，就恩格斯概括所引用的例子来看，恩格斯所指的物理常数，主要是那些引起物质的物性和现象变化的临界值，如熔点、沸点、汽化点等，所以他认同黑格尔的观点，认为“化学可以被称为研究物体由于量的构成的变化而发生的质变的科学。”
现在看来，更多的物理常数并不表示物质的临界值，如折射率、电阻率、介电常数等。从物理学的角度看，物理常数就是那些用来反映不同层次物质属性及其效应的一些数值，它们具有一定的稳定性，可以用来建立物理量之间的数量关系，区分不同的物质，即物理常数是反映物质客体物理属性的不变的或相对不变的数，它们不仅有临界值，还有极限值等。
然而物理常数不会仅局限于表示物质的性质，随着人们认识的提高，物理常数会超越具体的物质，表现出某种普适性，反映物质世界的一般性质，成为物理学的理论基础。如光速，开始只是作为光运动的属性进行测量，因为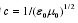
的发现，将光与电磁统一起来，光速表示了所有电磁运动在真空中的速度，随着光速不变性的发现，光速又成为狭义相对论的理论前提，成为一个普适常数。根据物理常数的普适性，人们通常将物理常数分为一般物理常数和基本物理常数。一般物理常数亦称物质常数与物质所处的具体环境相关，原则上量子力学已可以对它们进行解释。如固体比热，爱因斯坦将固体等效成平均能量为 hw 的 N 个相同的谐振子，考虑每个振子有三个维度，推得固体比热为：
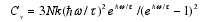
其中 k 是玻尔兹曼常数，τ=kT。该式在 T 足够大时，可得到 Cv=3Nk 的推论，即杜隆-珀替定律，并解释了固体比热在 Tà0 时，Cvà0 的特性。这个比较粗糙的理论，在物理学史上，揭开了量子力学应用于固体物理学的序幕。由此我们可以认为一般物理常数不是真正的物理常数，它们可以用量子理论解释。
因为物质本身的复杂性，以及与环境相互作用的不易确定性，我们对一般物理常数的解释也是有限的。
如固体间的摩擦系数 μ，虽然我们能够分析出许多形成摩擦系数的因素，然而至今仍无法确定各种因素是如何作用的，因此主要还是依据唯像的公式进行测量，这样做并不影响实际运用，表明物质的微观结构及其运动具有宏观的收敛性，是各层次物质存在自身规律性及其层间偶合不强或脱偶的依据。但毕竟我们已有了原则上的解释手段，因此在理论上并为其烦恼。但是对于基本物理常数（以下简称“物理常数”），也称普适常数或自然常数，却不断地困绕着物理学家，因为“至今还没有人成功地预测或解释过任何自然常数……”至今这种情况仍没有多少改变，因此成为本文的讨论对象。
2、 解释物理常数的动机
据传泡利一生始终感到奇怪，为什么无单位的精细结构常数的近似值为 1/137。他得病住入苏黎世的红十字会医院后，有一次他的助手去看望他，他就问他的助手：“你看到这间房的号码了吗？”他的病房号码恰好是 137。故事有些宿命，但它所引出的问题值得深思。物理常数难于解释，是什么原因推动物理学家要解释它们呢？
2.1 物理常数的基础性
物理理论的重大发展，总是与一个物理常数有关，它们构成了物理学理论框架的结构性基础。如牛顿力学与万有引力常数 G 有关；电磁理论及至后来的狭义相对论与光速 C 有关；量子力学的产生与发展与普朗克常数 h 有关，以至于有学者据此将物理学划分为三个发展阶段。物理学家对物理常数的基础性有着深刻的印象，因此他们会在物理学理论的研究中，尝试引入或构造新的物理常数，如爱因斯坦在其引力场方程中引入宇宙常数；海森伯曾尝试通过构造新的物理常数建立统一理论。
2.2 物理常数的启发性
物理常数有着与宇宙及其物质可能的构成与演化相联系的特质，因此它们的发现总能给物理学家以富有想象的启发。如在精细结构常数刚发现时，物理学家认为 1 /a可能是个精确的整数 137，由此引起的丰富想象启发着他们去研究，物理学家派斯曾这样回顾当时的历史：“这个数字引起了人们许多的冥思苦想、不眠长夜和离奇幻想……论证这个物理学上最大笑话的文章，居然溜过一家一流物理学期刊编辑的审查被发表出来。”
精细结构常数受到如此重视的主要原因是它分别由涉及电动力学（e）、相对论（c）和量子力学（h ）的三个重要常数简单组合的无量纲成常数。无量纲常数本来就引人注意，爱因斯坦就认为无量纲常数才是真正的常数，因为它们不仅与具体物质无关，而且还与取什么物理单位制没有关系，因此更能引起物理学家关于现存宇宙可能存在深层原因的丰富联想，启发物理学家去发现它们所携带着的可能的关于物质世界的深层信息。
2.3 物理常数的认识性
物理常数有着超越或颠覆传统观念或理论的认识作用，如电子电量与质量的被测量，证实了原子的可分性，使人们对物质及其结构产生突破性的新认识，开启对原子结构及其更基本的粒子研究；光速不变性的发现，创建的狭义相对论，使人们对时空有了更深入的认识，并发现超乎现象的质量和能量之间的关系。物理常数的认识作用，通常还反映在由对它们的不断认识引起的人们的自然观改变，有学者认为，普朗克常数从自然界由连续走向间断、由主客独立走向主客相干和宇宙由确定走向不确定三个方面改变着人们的自然观，“促使人们从经典物理学的世界图景中走出来而从根本上改变对自然界的法。”
2.4 物理常数的普适性
普适性是物理常数最基本的特性，它建立在物理常数恒常性的基础之上。物理学家认为，一旦物理常数的恒常性不成立，则将是整个物理学的危机，至少表明在物理常数恒常性失效的地方，已知的物理学理论也将自动失效。然而物理学家们并不放心物理常数的恒常性，因为他们并不知道恒常性是否可靠。为此，物理学家们不断提高物理常数的测量精度，以便从中发现蛛丝马迹，并将目光从实验室投向宇宙空间，探测宇宙早期的信息，但至今仍不能确定物理常数是否变化。在测量的基础上，他们更希望能发现第一性原理，并由第一性原理给出物理常数的“恒常性”解释。
3、 物理常数解释的几种尝试
物理常数所具有的上述特点，对物理学家们的诱惑是不言而喻的，再加上已发现的物理常数间存在的相关性和统一性等特征，使得物理学家们要想尽办法得到对它们的解释。以下是其中较为典型的几种：
3.1 从数字本身寻找物理常数的解释
数字自古能唤起人们某种神秘的心理反应，用数字猜测命运是其中较为典型的表现，这种迷信方法，在现代世俗生活中仍有残余。在科学史上，有着神秘主义倾向的古希腊毕达哥拉斯学派认为“万物皆数”，他们对“数”产生极度虔诚的信仰，这在今天看来有些可笑。然而就是这一个学派奠定了现代数学的基础，并发现具有后来物理学数学化特征的谐和音程与不同弦长之间有整数比例的关系，被人们称为毕达哥拉斯律制。因此，如果剥去对数字的迷信部分，以及对数字的实在化问题，对数字本身的分析也可算作一种研究和解决问题的方法。部分物理学家结合自身的物理思想与经验，就曾运用这种方法，试图对物理常数进行解释，如爱丁顿以其对相对论的熟悉与偏好，通过对四维空间的大胆构想，对精细结构常数进行了被同行斥之为“数字学”的分析，认为：
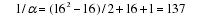
他的研究发表后曾遭到同行嘲笑，前文派斯所说的“物理学的最大笑话”，大概就是指这件事。用这种方法解释物理常数，还没有成功案例。
3.2 运用组合法获得物理常数的解释
用几个已知物理常数的简单组合，先于物理理论与测量构造出可能的新物理学常数，在启发物理学研究的同时，尝试理解和解释物理常数。这种方法的合理性在于：（1）物理学的发展并不是旧理论逻辑的结果，物理学研究也需要或然性的思维方法；（2）部分物理常数间的确存在着简单的数学关系，如精细结构常数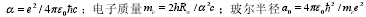
等，它们不仅可以从其它物理常数中导出，而且它们本身又具有明确的物理意义，可以通过实验独立测定。在看似不成逻辑的物理常数间存在着严密的数学关系，是令人惊奇的，它们极其自然地揭示着物质之间存在的联系，说明物理常数存在某种自恰性，对此已有学者进行研究，他们认为一个物理常数，可以由π、自然常数 e 和其它基本物理常数组合来计算。
在用组合法构造的物理常数中，比较有影响的是由普朗克和狄拉克两位物理学家提出的。普朗克在 1912 年用 G、h、c 构造了自然界中空间、时间和质量的基本值，其中质量的基本值已认为有着确切的物理意义，它是核力场的场量子--引斥子的质量，其它还处于猜测中。普朗克质量所具有的能量与普朗克空间、时间和质量组合的能量值2(/)pppmlt具有相同的数量级，也令人遐想，其约为质子能量的1910倍，所显示的“小而强”特征，可猜测与宇宙的早期相联系。由于普朗克常数所具有的物理意义，它们已被列入物理常数；狄拉克 1937 年 2 月在《自然》杂志发表了一篇短文，提出了自己的宇宙学观点，给出了三个无量纲的组合常数，即大数假设。大数假设得出了一些诱人的推论，并对万有引力常数 G 提出了一种解释，认为它与时间 t 成反比例。然而因为缺少实验的支持，大数假设，至今还是个迷。组合法为物理学提出了一些有前瞻性的问题，启发着物理学研究，但基本上只是一些猜测，因此不可能给物理常数提供完善的解释。
3.3 用人择原理对物理常数进行解释
人择宇宙的思想可以追溯到上千年前的古代，然而用来解释宇宙的起源、演化和结构，是由美国物理学家 R·H·迪克在 1961 年首先提出来的。在迪克人择理论的基础上，现在已演化出多个版本，其中主要的有弱人择原理与强人择原理，前者即是迪克的人择宇宙理论，后者由英国物理学家 B·卡特提出。弱人择原理认为，在一个大的或具有无限空间和时间的宇宙里，只有在空间和时间有限的一定区域里，才存在智慧生物发展的必要条件。根据弱人择原理由智慧的演化的必要条件，估算了宇宙大爆炸发生的时间，并成功的推算出狄拉克的“大数假设”。强人择原理认为，存在多个宇宙或单一宇宙的多个不同区域，在我们的宇宙或区域中之所以有这些巧合的常数，是因为只有当这些常数具有现在为我们的实验所测得的数值时才会有人类存在。由强人择原理出发，物理学家们惊奇的发现，原子和分子的结构几乎完全由电子和质子的质量比，以及精细结构常数来控制，它们稍微有点变化，有序的分子结构就不存在，生命需要的碳原子就不稳定，DNA 的复制就会消失，恒星不能够燃烧氢和氦……以至于霍金惊呼：“这些数值看来是被非常细致地调整到使得生命的发展成为可能。”
然而人择原理只是对观察结果的可能推测，而不是物理学解释，甚至与解释物理常数没有关系，因为它不能导致建立关于物理常数的物理学方程，并给出预言。
3.4 寻求统一理论对物理常数的解释
统一理论的建立，必以某个第一性原理为前提，因此统一理论可以为物理常数提供完美的解释，所以霍金说：“也许有一天，我们会发现一个将它们所有都预言出来的一个完整的统一理论”。
在各种统一理论中，弦/M 理论无疑是最受物理学家追捧的。从弦理论到 M 理论，已经过二次革命。其第一次革命是在 1984 年秋提出超弦理论，解决了弦理论存在的 25 维、快子和强子无质量等问题，但不久就发现在 10 维空间里，超弦存在着 5 个相对独立的且和谐的理论，对它们使用卡丘空间处理了额外的 6 维后，每个超弦理论仍需要标志不同几何特征的数百个常数，因此不但不能解释物理常数，反而使问题变得更加复杂；第二次革命发生在 1995年，著名的美国物理学家威藤在一次洛杉矶弦论会议上提出了一个用有着 11 维的 M 理论，来统一 5 个超弦理论设想，并认为它们其实是同一个理论，然而直到现在也没有在其上建立起合适的物理学方程，产生任何可观察的实验预言，因此也不能给出物理常数的解释。对此美国著名物理学家 L.斯莫林认为：“M 理论的关键问题就在于寻找一种能与量子力学理论和背景独立性相容的形式……遗憾的是，这方面几乎没有什么进展。有一些迷人的线索，但我们还不知道 M 理论是什么”。因此物理学家对弦/M 理论的前提产生怀疑，他们被分为乐观派和悲观派，其中不乏反对的声音。
4、 对物理常数解释的思考
伽莫夫曾说过，对物理常数的认识便构成未来物理学。对物理常数的解释的困难，表明我们对物理常数还存在严重的认识问题，这就需要对如“什么是物理常数的解释”，“物理常数能不能解释”，“怎样才能解释物理常数”等基本问题进行思考。
4.1 关于物理常数的解释
对于物理常数的解释，如果只是阐明其物理意义，则问题会简单得多，如光速可由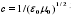
计算，表示光是电磁波，该式表达了电磁波在真空中的速度。即使后来认识到它的不变性，以及是一切物体的速度极限，那也是可以述说的。但如果问及它的速度为什么是这个值，是否可能变化，是否有超光速存在，以及它为什么可以用两个真空电磁常数确定等时，问题就来了，就不容易讲得清楚，人们自然会联系到类似真空物质与结构等基本问题，需要更深层次的理论来解释。如果说像光速这样的有量纲常数，还可能采用合适的单位制进行协调的话，无量纲常数则更令人困惑。因此所谓物理常数的解释，就不仅是对物理常数的物理意义进行阐释，而且是使它们成为前文提到的某个第一性原理的逻辑结果，并逻辑地确定它们是否变化和如何变化。就此而言，弦/M 理论走的是一条解释物理常数的进路，然而物理学的统一性在没有证实之前，也只是假设，过于追求美妙的理论建构，就有脱离实验的危险，那就不是在做物理，而是在做哲学。通常人们认为科学是问“怎么样”，而哲学是问“为什么”的，在笔者看来，并不是这样的，至少物理学不是这样的。物理学是既问“怎么样”，也问“为什么”，因为物理学一边关注着经验现象，一边用理论思维。
4.2 物理常数可以被解释的理由
前文提到，随着量子理论的发展，在原则上使一般物理常数得到解释，而在量子理论的历史上，也曾有里德伯常数被玻尔理论所解释的案例。因此物理常数原则上是可以解释的，但前提是有更深层的物理学理论发现。随着非线性等复杂物理学、量子理论的研究发展，以及对不同层次物质存在的脱偶现象的认识，使得物理学的研究也在采用生成论、整体论和层创论等思想方法进行思考，但还原论仍应是物理学研究的基本方法，尤其在涉及像物理常数解释这样的基本问题时。还原论是基于复杂性背后存在简单性的信仰，按照还原论的思想方法，发现更深层次的物理学，就如同哲学的追溯不断“后退”，从对现有的物质认识中，发现更基本的物质基元及其相互作用力。物理学的这种发展模式似无止境，然而人们有理由相信第一性原理的存在，并由此建立统一理论，最后使物理常数得到合适的解释。这不仅是因为人类对可理解性的信仰，而且是因为：（1）牛顿物理学及其之后的物理学，事实上走过的是一条统一之路；（2）物理学在宇观和微观领域的研究进展，不断表明它们正辩证地汇合于早期宇宙；（3）物理常数可能是早期宇宙演化的结果，说明着宇宙存在真正的开端。然而这也可能正如康德所认为的，“心灵独特的活动是综合并统一我们的经验”，人在为自然界立法，但这就是物理学的认识之路，除非有一天统一之路被证否。
4.3 物理常数可能被解释的逻辑
物理常数解释的逻辑，本质上也就是物理学研究的逻辑。由于物理学研究物质世界最基本的结构与规律，因此当对它的基本问题进行研究时，某些哲学观念就会呈出来，前文提到的“第一性原理”就有着哲学中的“本体”意蕴，不小心很容易让人滑入形而上学的思辨。因此要进行物理常数的解释，首先要回到物理学的研究逻辑，其中主要有：（1）更深层次物理学理论的发现，发生在已有理论的适用边界上。这时有充分的观察数据和发现大量的反常现象，为此多数物理学家开始进行新理论的建构，甚至有局部的合理的理论出现；（2）在大量观察数据或反常现象出现的基础上，新物理理论的建立，通常还要等待某些关键环节的发现。
如狭义相对论中光速不变性的发现，量子力学中作用量子的发现等。目前相对论与量子理论尽管存在一些理论问题，但并没有走到理论的适用边界，因此它们的统一问题，有待于进一步的反常发现，以发现“关键环节”；（3）寻找“关键环节”，要物理理论为物理实验提供可操作的预言，同时物理理论要接受物理实验的检验，并在此过程中产生思维方式的飞跃。发现与旧理论通常并没有逻辑联系，因此建构物理理论只是现象，本质上是物理理论与物理实验辩证运动的结果，是思维对现象背后实在的把握。正因为这样，基于不同物理思想所建构的物理理论，可以殊途同归，如海森伯、薛定谔与费曼等人不同的量子力学程式的等效性即是例证，这是物理学理论具有客观性的基础。
参 考 文 献：
[1] 王竹溪.基本物理常数的概况及其在物理学中的作用[J].物理,1973,2(2):100.
[2] 罗素.张金言译.人类的知识[M].北京:商务印书馆.1989.
[3] 乔治·伽莫夫.高士圻译.物理学发展史[M].北京:商务印书馆,1981.
[4] 恩格斯.于光远等译.自然辩证法[M].北京:人民出版社,1984.
[5] 王飞,胡秀华.物理常数的分类[J].齐齐哈尔师范学院学报(自然科学版),1992,12(1):51.
[6] John D.Barrow,John K.Webb.变化的常数[J].科学,2005(8):27-28.
[7] 阿伯拉罕·派斯.关洪,杨建邺译.基本粒子物理学史[M].武汉:武汉出版社,2002.
[8] 约翰·巴罗.陆栋译.大自然的常数[M].上海:上海世纪出版社,2006.
[9] 张晶.普朗克常数 h 引起的经典物理学自然观的三种改变[J].自然辩证法研究,2007,23(2):45-46.
[10] 杨福家.原子物理学（第三版）[M].北京:高等教育出版社.2000.
[11] 王涛,刘胜洪.关于基本物理常数之间的定量关系[J].中国组织化学与细胞化学杂志,2012,21(6):603.
[12] 汪世清.淡普朗克质量[J].物理,2002,31(5):303.
[13] 史蒂芬·霍金.时间简史--从大爆炸到黑洞[M].湖南:湖南科学技术出版社,1996.
[14] L·斯莫林.物理学的困域[M].湖南:湖南科学技术出版社,2008.
[15] 冯端.漫谈物理的过去、现在与未来[J].物理,1999,28(9):524.
[16] S·E·斯通普夫,J·菲泽. 西方哲学史--从苏格拉底到萨特及其后(第 8 版)[M].北京:世界图书出版公司,2009.
