磁转动。磁转动[51]是原子核转动研究中继回弯现象、超形变转动带之后的又一重要成果。与通常的高自旋态和超形变转动带不同,磁转动带通常发生在近球形或弱形变原子核中。如果有一个高j-壳的中子(或质子)粒子,同时有一个高j-子壳的质子(或中子)空穴,在转动带带首,质子和中子角动量近乎相互垂直,两者耦合的结果使总角动量矢量倾斜于原子核的惯性主轴。由于系统的形变很小,要获得角动量,最可能的结果是质子和中子的角动量互相靠拢,而总角动量的方向变化不大,从而可以形成规则的转动谱。由于质子和中子角动量就像一把正在合拢的剪刀,因此又把这种转动带形象地称为“剪刀带”.由于质子和中子的g-因子符号相反,所以在垂直于总角动量的平面内的流分布会产生一个很大的磁偶极矩垂直分量。此时,原子核的转动便可以看成是绕着总角动量所在方向,原子核磁偶极矩的转动,转动过程中会向外发射磁偶极辐射,因此称作“磁转动”[51].原子核的磁转动特征通常表现为规则的、由磁偶极(M1)跃迁联系的、
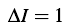
的转动谱。
文献[52]发展了三维的倾斜轴推转协变密度泛函理论,数值计算程序只包含了空间的反射对称性,导致计算过程非常复杂,实际运用的难度很大,仅被用于研究
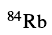
的磁转动带。但是,这是第一次将协变密度泛函理论用于研究磁转动。它的成功表明密度泛函理论也可以很好的描述磁转动特征。文献[53]发展了专门用于研究磁转动带的倾斜轴推转协变密度泛函理论程序。针对磁转动的特性(转动轴位于一个主轴平面内),在所发展的程序中,不仅考虑了空间反射对称性,还考虑了体系在垂直于转动轴所在平面的主轴方向的对称性。因此,整个数值计算过程相较于文献[52]有很大程度的简化。在此基础上,利用点耦合的有效相互作用代替介子交换有效相互作用[54],可以进一步简化计算的复杂性,广泛用于研究磁转动[55]和反磁转动[56],相关工作可以参见综述文献[57].
关于原子核转动的研究,还可以参见王守宇[58],徐文强等人[59],以及亓斌等人[60]的文章。
4原子核手征对称性
手征对称性是物理学等自然科学中的一个重要现象。 1997年,文献[61]预言高速转动原子核中的手征对称性自发破缺,其实验特征为手征双重带,即原子核转动谱中存在宇称相同、角动量相差、能
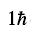
级近似简并、电磁跃迁性质类似的两条转动带。这一预言于2001年被实验证实[62],从而使得原子核手征对称性研究成为核物理的热点领域之一。中国科学家在手征对称性的实验研究中,也作了很好的工作。例如,发现最轻质量区A~80的第一例手征对称性原子核[63]和
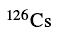
中的手征双重带现象[64,65].
手征对称性的多样性--
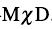
。为了微观描述原子核的手征对称性,预言新的物理现象,文献[66]进一步发展协变密度泛函理论,利用绝热近似和固定组态约束方法,预言了原子核手征对称性破缺的多样性,其实验信号为一个原子核中存在多对手征双重带,并将这一新现象命名为Multiple Chiral Dou-blets,
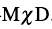
。
经过理论和实验同行多年的合作和努力,美国、匈牙利、德国和南非等国科学家分别在美国阿贡国家实验室、伯克利国家实验室和南非i Themba国家实验室进行实验探索。以美国圣母大学为主的实验合作组,分别于2008年和2011年在阿贡国家实验室进行两次实验,并于2012年访问北京大学进行合作,成功确认
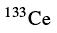
中存在两对手征双重带,证实了
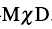
的理论预言,论文以“Evidence for Multiple Chi-ral Doublet Bands in
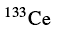
”为题在美国《物理评论快报》上发表[67].
南非,德国和中国等国科学家早在2010年2月,向南非i Themba国家实验室提出实验计划,探索
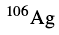
中存在
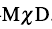
的可能性。虽然在
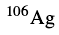
没有发现
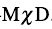
,但是成功解决了
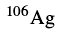
的手征疑难问题[68].
匈牙利和中国等国科学家不仅成功确认
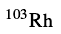
中存在
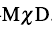
,而且指出
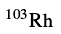
中的
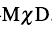
建立在相同组态之上[69].
如果手征双重带的观测证实了原子核存在手征对称性的话,那么理论
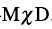
预言的实验证实,更进一步提供了原子核存在三轴形变以及手征对称性的有力证据。
关于原子核手征对称性研究的理论进展,陈启博会在本专辑中进行介绍[70].
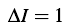 的转动谱。
的转动谱。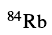 的磁转动带。但是,这是第一次将协变密度泛函理论用于研究磁转动。它的成功表明密度泛函理论也可以很好的描述磁转动特征。文献[53]发展了专门用于研究磁转动带的倾斜轴推转协变密度泛函理论程序。针对磁转动的特性(转动轴位于一个主轴平面内),在所发展的程序中,不仅考虑了空间反射对称性,还考虑了体系在垂直于转动轴所在平面的主轴方向的对称性。因此,整个数值计算过程相较于文献[52]有很大程度的简化。在此基础上,利用点耦合的有效相互作用代替介子交换有效相互作用[54],可以进一步简化计算的复杂性,广泛用于研究磁转动[55]和反磁转动[56],相关工作可以参见综述文献[57].
的磁转动带。但是,这是第一次将协变密度泛函理论用于研究磁转动。它的成功表明密度泛函理论也可以很好的描述磁转动特征。文献[53]发展了专门用于研究磁转动带的倾斜轴推转协变密度泛函理论程序。针对磁转动的特性(转动轴位于一个主轴平面内),在所发展的程序中,不仅考虑了空间反射对称性,还考虑了体系在垂直于转动轴所在平面的主轴方向的对称性。因此,整个数值计算过程相较于文献[52]有很大程度的简化。在此基础上,利用点耦合的有效相互作用代替介子交换有效相互作用[54],可以进一步简化计算的复杂性,广泛用于研究磁转动[55]和反磁转动[56],相关工作可以参见综述文献[57].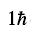 级近似简并、电磁跃迁性质类似的两条转动带。这一预言于2001年被实验证实[62],从而使得原子核手征对称性研究成为核物理的热点领域之一。中国科学家在手征对称性的实验研究中,也作了很好的工作。例如,发现最轻质量区A~80的第一例手征对称性原子核[63]和
级近似简并、电磁跃迁性质类似的两条转动带。这一预言于2001年被实验证实[62],从而使得原子核手征对称性研究成为核物理的热点领域之一。中国科学家在手征对称性的实验研究中,也作了很好的工作。例如,发现最轻质量区A~80的第一例手征对称性原子核[63]和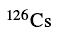 中的手征双重带现象[64,65].
中的手征双重带现象[64,65].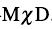 。为了微观描述原子核的手征对称性,预言新的物理现象,文献[66]进一步发展协变密度泛函理论,利用绝热近似和固定组态约束方法,预言了原子核手征对称性破缺的多样性,其实验信号为一个原子核中存在多对手征双重带,并将这一新现象命名为Multiple Chiral Dou-blets,
。为了微观描述原子核的手征对称性,预言新的物理现象,文献[66]进一步发展协变密度泛函理论,利用绝热近似和固定组态约束方法,预言了原子核手征对称性破缺的多样性,其实验信号为一个原子核中存在多对手征双重带,并将这一新现象命名为Multiple Chiral Dou-blets, 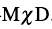 。
。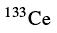 中存在两对手征双重带,证实了
中存在两对手征双重带,证实了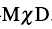 的理论预言,论文以“Evidence for Multiple Chi-ral Doublet Bands in
的理论预言,论文以“Evidence for Multiple Chi-ral Doublet Bands in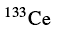 ”为题在美国《物理评论快报》上发表[67].
”为题在美国《物理评论快报》上发表[67].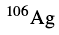 中存在
中存在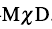 的可能性。虽然在
的可能性。虽然在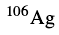 没有发现
没有发现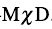 ,但是成功解决了
,但是成功解决了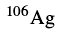 的手征疑难问题[68].
的手征疑难问题[68].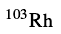 中存在
中存在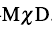 ,而且指出
,而且指出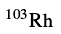 中的
中的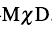 建立在相同组态之上[69].
建立在相同组态之上[69].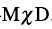 预言的实验证实,更进一步提供了原子核存在三轴形变以及手征对称性的有力证据。
预言的实验证实,更进一步提供了原子核存在三轴形变以及手征对称性的有力证据。




