2. 2 “绝对空间”以太
在爱因斯坦看来牛顿力学中还存在着未直呼其名的“以太”,它被称为“绝对空间”[1].在牛顿第二定律中包含加速度的概念,然而运动物体的加速度不能完全用尺子和时钟所作的测量决定。确定加速度,除了需要测量两点之间的距离、时间,还需要一个处于适当运动状态的坐标系( 惯性系)。如果坐标系选择不恰当( 如非惯性系) ,则牛顿第二定律不成立。可见,在牛顿第二定律中运动物体所在的环境,也就是空间,以一种隐而不宣的方式成为客观实在。牛顿进一步赋予空间特殊性质: 与外界任何事物无关永远是相同的和不动的[6,7],将之称为“绝对空间”.
以“绝对空间”为内涵的以太在爱因斯坦建立狭义相对论革新了人们的时空观后,已被人们放弃。
3以太在光学中的发展
光的本性问题是光学的基本问题,以太以新的内涵---作为承载光波的介质,在这一问题上曲折发展。胡克(R. Hooke,1635-1703) 和惠更斯(Huy-gens,1629-1695) 认为光的本性是波[8,9].由于当时人们只认识机械波,而机械波必须有承载波的介质,因此当时的波动说认为光的承载介质就是以太,用以解释光可以穿过抽出空气的玻璃管,即光可以在没有空气的真空中传播的事实。此时,以太以承载光波介质的内涵在光学领域获得了新生。
由于波动说还可以解释光有不同颜色的原因是波的振动频率不同,而微粒说可以解释光的直线传播。从而,需要以太的波动说和不需要以太的微粒说,在当时关于光的本性的争论中处于势均力敌的状态。
然而,由于牛顿支持微粒说[10],随着牛顿在物理学界威望的增长,光的微粒说压倒了波动说,作为波动说的基石---以太的理论也随之处于低潮。
1807年,托马斯·杨(Thomas Young,1773-1829) 设计了着名的双缝干涉实验,并用波动说完美地进行了解释。菲涅耳(Fresnel,1788-1827) 则采用了光的波动说并成功地解释了光的偏振。这使光的波动说重新占据上风,也使光的承载介质---以太的地位得到了巩固[8].
随着光学的发展,对光的性质及其规律的认识也逐渐丰富和深化。人们慢慢认识到光是横波,且光速达到了
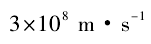
,依据弹性力学,承载光波的介质以太应该是坚硬的固体。然而,无处不在、坚硬的固体以太却不能阻挡来自遥远星球的星光来到地球,这是令人难以置信的。这使得作为承载光波的介质的以太又一次受到大家的质疑[11].一直到人们认识到光的本质是电磁波,这一基础问题才在电磁学和电动力学的框架下得以解决。
4以太在电磁学和电动力学中的发展
对电荷相互作用的机制问题,反对超距作用观点的法拉第(Michael Faraday,1791-1867) 提出了“场”的概念,这里的“场”是一种无处不在的、没有质量的弹性以太[12].以太开始进入电磁学。然而,其内涵与在力学中发展起来的传递相互作用的介质以太完全相同。
1865年,英国杰出的数学物理学家麦克斯韦(Maxwell,1831-1879) 建立了麦克斯韦方程组,根据方程组可以推导出电磁波的波动方程,并求得电磁波在真空中的波速是
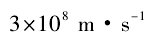
,与实际测得的光速一致,基于此事实麦克斯韦作出了光的本质是电磁波的预言。该预言由赫兹(Hertz,1857-1894) 于1887年证实。那么自然可以认为“承载光波的介质以太”就是此处的“承载电磁波的电磁以太”.
另一方面,当人们考察麦克斯韦方程组的参考系问题时发现: 从麦克斯韦方程组出发可以得到真空中的波动方程,并且波的传播速率为光速。依据当时的物理学原理,这意味着麦克斯韦方程组只对一个特殊的惯性系成立,而对相对这一惯性系匀速运动的其他惯性系不成立。这一特殊的惯性系被称为绝对静止参考系,人们认为绝对静止参考系就是以太。显然,这里的绝对静止参考系以太与牛顿力学中绝对空间以太的内涵相同。
此时,以太学说在物理学不同分支学科的发展随着这些学科的成熟而开始走向融合统一的道路。以太在经典物理学中的核心内涵有三: 绝对静止参考系,传递相互作用的介质,承载电磁波传播的介质。
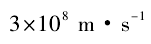 ,依据弹性力学,承载光波的介质以太应该是坚硬的固体。然而,无处不在、坚硬的固体以太却不能阻挡来自遥远星球的星光来到地球,这是令人难以置信的。这使得作为承载光波的介质的以太又一次受到大家的质疑[11].一直到人们认识到光的本质是电磁波,这一基础问题才在电磁学和电动力学的框架下得以解决。
,依据弹性力学,承载光波的介质以太应该是坚硬的固体。然而,无处不在、坚硬的固体以太却不能阻挡来自遥远星球的星光来到地球,这是令人难以置信的。这使得作为承载光波的介质的以太又一次受到大家的质疑[11].一直到人们认识到光的本质是电磁波,这一基础问题才在电磁学和电动力学的框架下得以解决。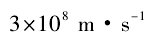 ,与实际测得的光速一致,基于此事实麦克斯韦作出了光的本质是电磁波的预言。该预言由赫兹(Hertz,1857-1894) 于1887年证实。那么自然可以认为“承载光波的介质以太”就是此处的“承载电磁波的电磁以太”.
,与实际测得的光速一致,基于此事实麦克斯韦作出了光的本质是电磁波的预言。该预言由赫兹(Hertz,1857-1894) 于1887年证实。那么自然可以认为“承载光波的介质以太”就是此处的“承载电磁波的电磁以太”.




