
脱氧核糖核酸具有重要的生物学功能,是DNA 到蛋白质间遗传信息的中间传递体.RNA 二级结构是特定平面图,配对的部分构成局部的双螺旋结构,这就是 RNA 的二级结构,它是一种平面的结构.
它的各种功能往往受到脱氧核糖核酸的结构的影响,因此脱氧核糖核酸的结构在一定程度上揭示着生命过程中 RNA 分子的作用,这些可以通过研究 RNA 的功能和结构间的关系.目前,使用实验方法在 RNA 信息数据的惊人的增长下,实现生物分子的具体的二级结构有着其自身的局限性,而且对所有分子并不是都有效的.
研究表明,对 RNA 二级结构预测,通过计算机仿真与数学建模的方法具有较高的可信度和参考价值,主要的类型有:
(1)动态规划的方法
动态规划方法是基于热力学原理. 当 RNA 在一个稳定的环境,自由能最小,我们可以理解为RNA 二级结构趋于稳定.最典型的是 Zuker 动态规划算法,是自由能计算模型.该算法实现简单,但它不能预测带假结的 RNA 分子,由于其真实结构可能不是最低自由能,所以用这种方法来预测准确率低.
(2)比较序列法
比较序列的方法通常采用的是共变模型和随机上下文无关语法模型.共变模型,首先通过小规模的比对,之后更大规模的子树和序列的比对概率被递归计算,直到得到最佳的比对.随机上下文是由一定的语法“句子”定义的规则,然后通过这些句子的分析,得到碱基配对关系的序列,从而使 RNA二级结构得到预测.通过比较序列的方法可以预测 RNA 二级结构更好,更准确,但他们需要更多的同源序列,并且对同源序列还有一定的限制要求,花的时间也较多.
由于上述方法的局限性,组合优化算法被提了出来.通过使用这种方法,遗传算法、模拟退火算法、Hopfield 神经网络等启发式算法被用来解决这类问题.本文提出了一种混沌 Hopfield 神经网络算法,将其应用于 RNA 二级结构的预测.
1、 免疫算法
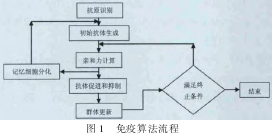
免疫算法(Immune Algorithm, IA)是一种进化算法,其灵感来自人体的免疫系统.该算法模拟人体免疫系统,是求解全局最优解的一种新的优化算法.记忆性和多样性机制,使免疫算法的具有良好的全局优化能力,很容易与其他方法结合,并得到很好的应用.免疫算法主要由以下几个部分构成:
抗原:免疫算法中,抗原对应目标函数和约束条件.
抗体:免疫算法中,抗体对应问题的解,可以随机产生一组解,也可以使用特定的方法赋予一个初始解.
免疫记忆:与抗原有最大亲和力的抗体加给记忆细胞.由于记忆细胞数量有限,新产生的与抗原亲和力较低的抗体将被替换为亲和力较高的抗体.
在免疫算法中体现为较低亲和力的解被替换为较高亲和力的解.
免疫调节:高亲和力抗体和高密度抗体分别受到促进和抑制.在免疫算法中体现为在实施抗体的选择过程中通过计算抗体存活的期望繁殖率.
通过下图 1 可以清楚的看出免疫算法的一般步骤:
2、 Hopfield 神经网络
Hopfield 神经网络称为单层反馈网络因其是一个只有单一的神经元层次的结构,同时每个神经元与其他神经元的输出是相互连接的.0 或者 1 是Hopfield 神经网络的取值集合,yi(t+1)是神经元的输出,xi(t+1)是网络的输出,如公式(1):

其中,Hopfield 的输出值保持为 0 或 1 是通过激励函数实现的.Hopfield 神经网络在优化计算的应用中,目标函数有相应的能量函数,从而网络权值也被确定,当神经网络的能量达到最小时的解,就是问题的最优解.
3、免疫 Hopfield 神经网络
(IA-DHNN)优化算 法求解。
3.1 RNA 二级结构中的 Hopfield 神经网络
Hopfield 神经网络用于 RNA 二级结构预测问题时,用基于最小自由能思想的茎区自由组合算法时,由于 vi=0 表示该神经元被选中,能量函数可以写成:
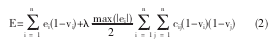
其中,cij即为节点 i 和 j 间的权值,茎是否被选中决定了 vi取 0 或 1,ei表示茎 i 的能量;茎 i 与 j是否相容来决定取值为 0 或 1;非稳定茎和稳定茎间的相对率通过 λ 调整.同时,第 i 个神经元的动力方程为:
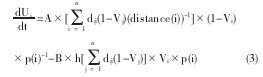
其中,dij取值 0 表示边 i 和边 j 不相交,取值为1 时表示边 i 和边 j 相交.h(x)作为激励函数,只有当x=0 时,h(x)=1.茎区 x 环长度用 distance(x)表示.公式(3)中分为惩罚项和激励项,惩罚项的权值参数 A表示,激励项的权值用 B 表示.
3.2 IA-DHNN 算法描述
对于 Hopfield 神经网络来说,其对初始值的依赖性很强,因此本文使用距离函数和免疫算法的多样性产生初始解,对神经网络的初始解进行优化,其中免疫算法通过产生若干代种群后,对其进行聚类,使用聚类中心作为 DHNN 神经元的初始输出,更新其初始解和输出值.其具体步骤如下:(1)初始化,使目标函数和约束条件有相应的能量函数,问题的解为神经元的输出 vi,令神经网络参数 T=mmax,t=0;(2)使用距离函数计算初始解,初始化神经网络;(3)使用免疫算法产生 80 代抗体;(4)采用 K 均值算法计算从免疫算法计算所得抗体的聚类中心;(5)初始化神经网络,选取一个还未被访问的聚类中心,为该神经网络神经元的初始输出;(6)当 ui>0 时,vi=1,否则 vi=0.而 vi=0 说明该碱基配对;(7)使用公式(4)中的定义的更新 ui,vi;(8)当满足终止条件,即满足 ui(t+1)=ui(t)+△ui(t)△t 或者 △ui(t)或者 t=max,继续下一步,否则转(5);(9)计算当前解的目标函数值;(10)当聚类中心全部被访问过,停止计算,否则转(4);(11)从中选取使目标函数值最小的解.
4、 实验结果
4.1 评价标准
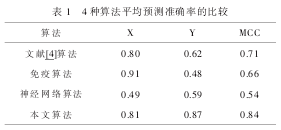
敏感性(X),特异性(Y)和马休兹相互作用系数(MMC)是目前评价 RNA 二级结构准确率主要的 3 个度量参数.X 和 Y 分别是指所有碱基对在真实结构中被正确预测到的比值和正确预测所有预测到的碱基对的比值.一般折中衡量上述两个参数的是 MCC.

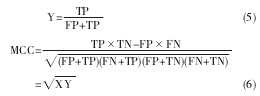
其中,TP 是碱基对正确预测的个数;FN 是碱基对在真实结构中存在,却没有被正确预测出的个数;FP 是碱基对真实结构中不存在,但被错误预测到的个数;TN 是不配对碱基被正确预测的个数.
4.2 参数设置和仿真结果比较
仿真中,A=0.1,B=0.2 为神经网络的常量参数.最后得到实验结果见下表 1. 我们可以看出本文的算法优于其他算法.
5、 结语
本文根据免疫算法多样性的有点,和神经网络对初值的依赖性,结合 tRNA 结构的保守性的特点,对神经网络的初值进行优化,将免疫神经网络混合算法首次运用于 RNA 二级结构预测,全局的搜索能力得到提高,使其不易陷入局部最优解,并获得一定的效果.
参考文献:
〔1〕林娟,钟一文,张骏.离散蛙跳算法预测 RNA 二级结构[J].南京师范大学学报(工程技术版),2011(04).
〔2〕邢翀.RNA 二级结构预 测算 法的 研究[D].吉 林大学,2012.
〔3〕林娟,钟一文.改进的免疫粒子群优化算法预测RNA 二级结构[J].计算机工程与应用,2012(01).





