摘 要: 审辨思维本质上是一种指向自我反思的思维方式。当前小学数学课堂中审辨思维的培养存在质疑批判等于挑毛病、破而不立、批判对象只针对他人的误区。针对这些误区可以给出如下策略:设计产生认知冲突的任务情境;依托数学推理活动培养审辨思维;构建“读懂别人-价值判断-发现问题-给出建议-自我反思”五步法。
关键词 : 审辨思维;核心素养;自我反思;
批判性思维(Critical Thinking)是21世纪4C核心素养之一,在我国刚刚发布的5C模型中翻译为“审辨思维”。5C模型提出的审辨思维包括质疑批判、分析论证、综合生成和反思评估四个要素。从这一界定可以看出,5C模型比4C素养更加强调了“反思”的重要性,将“能慎重考虑他人观点且尊重他人挑战自己观点的权利”纳入到审辨思维的特征之中,审辨思维“始于质疑,归于反思”。审辨思维重视“问题”意识的唤醒,注重生成解决问题的决策,指向“自我反思和成长”。然而,在数学教学中常常出现“为质疑而质疑”的场面,因此,我们须反思审辨思维培养中存在的问题并努力寻找教学方式上的突破。
一、小学数学课堂中审辨思维培养的误区
1.“质疑批判”等于“挑毛病”
独立思考、小组讨论、个人(小组)汇报、全班交流几乎是每节课都要用到的学习方式,在交流环节,教师常常以“这位同学的汇报有什么问题?你有什么建议?”这样的问题引发学生思维上的碰撞,同学们想方设法地去发现汇报者的不足之处,但是“审辨”需要长时间地、审慎地追问并寻找证据,课堂上并没有足够的时间让学生思考,常常是刚刚结束汇报就要求学生提出质疑,从而使“质疑批判”被简单地等同于“挑毛病”。这样不仅不能培养审辨思维,更容易误导学生陷入“思考等于挑毛病”的误区。
2.“破而不立”
“破而不立”并不是审辨思维的宗旨。在一次“比赛场次”课上,教师设计了实践活动,要求学生根据参赛人数、场地数量、比赛时间等实际情况分组设计比赛方案,各组分别设计了淘汰、单循环、单循环与淘汰混合等不同赛制,汇报时同学们纷纷指出其他组方案中存在的问题,如淘汰赛既费时又可能出现强者淘汰弱者升级的不公平现象,单循环赛公平但费时等,小组循环赛涉及如何分组才公平,一节课就在各组僵持中结束了。此时我们应引导学生思考:“公平是绝对的还是相对的?众多方案中哪一种最公平?对比自己的方案,别人方案有哪些可供自己借鉴之处?如果让你对其他方案提出建议,你是否有更好的办法?”从而找到相对公平、合理的方案。

3. 批判对象只针对他人
小学数学课堂上,培养审辨思维的方式多为“给别人提建议”,从而使“批判”对象经常指向他人。培养什么人,是教育的首要问题。数学课堂不能培养“只批判别人从不反思自己”的人,而是会合作、会沟通、会共同做事的人。5C模型将“Critical Thinking”翻译为“审辨思维”而不是“批判性思维”有助于我们澄清审辨思维的内涵,明晰审辨思维的自我指向性,在数学课堂上走出培养的误区,让学生养成善于倾听、勇于反思的良好思维品质。
二、小学数学课堂中审辨思维培养的策略
1. 设计产生认知冲突的任务情境
审辨思维的培养需要“好”的情境,让学生产生认知冲突的情境是好情境。好情境需要教师的设计,也需要及时抓住学生的生成。
如讲授一年级“百以内数的认识”时,教师设计了三个学习活动,其中第三个活动是“借助计数器数数——在计数器上从99拨到100”,活动中学生有如下几种表现。
表1 学习活动中学生的表现
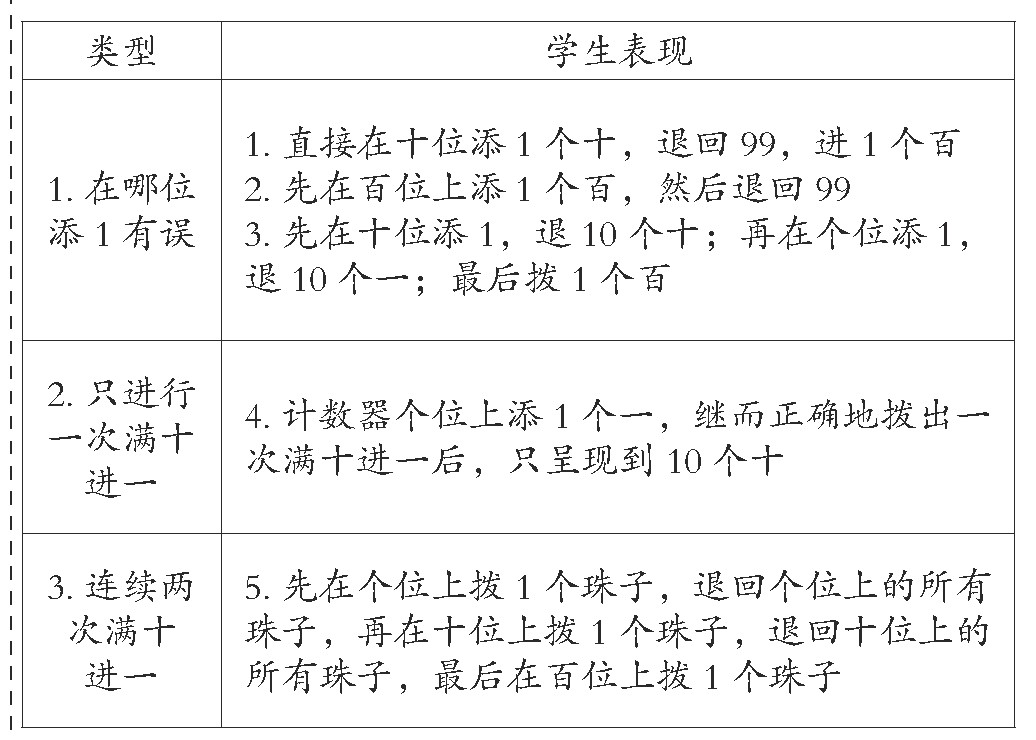
从结果来看,第1、2、3、5种方法最终计数器上呈现的都是“百位上有一个珠子”,但从学生拨珠子的行为来看却各不相同,学生的不同表现形成了“冲突”,也反映了学生在理解满十进一这一概念上的困惑。于是教师提出如下思考问题:“生1和生5有什么不同?生2和生5又有什么不同?你赞同哪一种拨法?满十进一体现在哪里?”教师把这些疑问抛给学生。学生相互交流后,找到了问题的本质:从99到100增加1个一,需要先在个位上加一,个位满10个一向十位进1个十,十位满10个十再向百位进1个百。生5的拨法能够体现这一过程。
本环节教师从学生的“冲突”出发,引导学生着眼于拨珠子的“过程”,对比不同方法,围绕本课的核心概念“满十进一”提出思考问题,引发学生的讨论,在讨论中达成共识,有效地锻炼了他们的审辨能力。
2. 依托数学推理活动培养审辨思维
由于审辨思维和数学推理活动都需要运用信息、数据、经验等进行“因为这样,所以那样”的推论,因此,可以将二者联系在一起。小学数学教材中有很多涉及到推理的内容,例如三角形内角和是180°、商不变规律等都运用了归纳推理,鼓励学生验证结论或说明道理时,学生实际上进行了演绎推理[1]。教师在数学推理活动中可以引导学生思考:“根据什么得出的结论?描述的过程合理吗?使用的方法恰当吗?”在这些问题的讨论中对得到的结论进行深度的、有逻辑的反思。在一节“三角形三边关系”的数学课上,教师设计了一个活动任务:以3厘米和4厘米的两条线段为两边画一个三角形,想一想第三条边的长度最长是多少?最短是多少?请说明你的想法。学生操作探究之后汇报:
生1:第三条边不能比7厘米再长了,再长的话就到平角了。
生2:最长边不能到7厘米,4厘米和3厘米加起来正好是7厘米,如果到7厘米就成了两条线,不能拼成三角形了。
生3:我们组有个疑问:虽然3厘米和4厘米加起来是7厘米,已经到极限了,会成为一个平角,但我们用尺子画却能画出来,是为什么呀?(其他几个组也表示有这个困惑)
生2:你们画的时候可能有误差,(进一步用小棍边摆边解释),当一个3厘米和4厘米小棍摆成平角时,第三条边怎么放,只能平着再来一条吧,那样就不能拼成三角形了。
……
继续讨论,学生又用同样的方法说明了第三条边最短也要大于1厘米(即其他两边之差)。在“说理”中学生逐渐明确了“三角形任意两边之和要大于第三边,任意两边之差要小于第三边”的性质,同时在讨论辨析中理解了背后的道理。本环节将学生的操作和推理过程相结合,培养了学生从多角度、多途径进行思考并阐明道理的能力。
3. 构建审辨思维培养五步法
基于审辨思维的四个要素,我们尝试构建数学课堂中“审辨思维”培养路径:“读懂别人—价值判断—发现问题—给出建议—自我反思”。
第一步,读懂别人。
读懂别人的想法是培养审辨思维的第一步,当我们从自我中心的角度进行思考的时候,很难理解他人的思想、感受和情感。我们常常在实践中犯了“我以为的就是你以为的”错误,对小学生来说,把自己对“数学”的理解清晰地呈现出来不是一件容易的事情,课堂上教师需要更多地给学生创造真实的“对话”平台,例如让学生学会使用“你说的是这个意思吗?我理解的对吗?你有什么补充?”等语言来确认对方观点。
第二步,价值判断。
我们有时会秉持“正误判断”的评价取向而不是指向自我反思的“价值判断”取向。进行价值判断既不能毫无依据地“鼓掌”,也不能一味否定,而是需要在读懂别人意图的基础上找到其对自己思考路径的价值,包括方向上的、方法上的,哪怕是失败的经验教训,有“证据”地对别人的做法和观点进行评判。
第三步,发现问题。
鼓励学生在发现问题的基础上进行“质疑”,提出自己“真正感到好奇的问题”。例如“我想知道……”而不是“难道不是……”等“暗含挑衅”的质问,这样的沟通与对话能够产生积极的影响,使得对话的双方不再简单地以非黑即白的方式思考问题,也让对话的双方有了围绕共同话题进行讨论和多角度思考的基础,为形成新的解决方案建立起“联合关系”。
第四步,给出建议。
思考者审慎追问、小心求证之后需要做出“决策”,这个“决策”是在对不同观点进行仔细分析后提出合理改进建议,是培养学生审辨思维的重要一步。值得注意的是,提建议时需要考虑到“对方的立场”,审辨思维需要进行思维的换位思考,即站在他人的角度思考问题,从而真正理解他人的观点。
第五步,自我反思。
培养审辨思维的最后一步是“自我反思”。要鼓励学生在评价他人的同时按照同样的标准评价自己,并不断追问:“别人的观点对我有启发吗?这一过程中我知道了哪些以往不知道的?我获得了哪些新的想法?我的观点还有哪些有待改进之处?”批判思想本质上具有自我批判的属性,“不论我们以为对自己的认识有多准确,都难免是在用自己的思维框架来认识自己的思维”[2]。从同伴对自己观点的反馈和他们所提出的不同视角中学习,有助于学生摆脱自我意识的“囚徒”困境,走向更高的审辨思维水平。
参考文献
[1]张丹推理能力的内涵及教学建议[J]小学教学:数学版, 2018(05):9-12.
[2]布鲁克菲尔德批判性思维教与学一帮 助学生质疑假设的方法和工具[M]钮跃增,译北京:中国人民大学出版社, 2017:35,52.





