摘要:基于课题研究,从学生经历活动的过程展开阐述,引导学生经历体验、感知、应用的过程,进而达成解题策略的形成,催生数学思考,建立数学模型。
关键词:解题策略; 体验感悟; 应用;
《义务教育数学课程标准(2011年版)》中对于问题解决给出了明确的界定:初步学会从数学的角度发现问题和提出问题,综合运用数学知识和其他知识解决简单的数学问题,发展应用意识和实践能力;获得分析问题和解决问题的一些基本方法,体验解决问题方法的多样性,发展创新意识;学会与他人合作、交流;初步形成评价与反思的意识。
小学一年级学生数学解题策略的教学实践研究,是针对学生的年龄特征,在培养学生学习习惯的同时,在尊重学生的基础上进行的以"数学解题策略"为核心的教学实践研究,强化学生解题的策略意识,并落实在平时的教学实践中。
一、经历活动的过程
就具体的数学策略而言,有两个过程:一是策略产生、发展和形成的过程,也就是说,这个策略是在什么时候用的,是问题情境;二是学生对策略的认知过程,即学生是怎么认识这个策略的。
笔者以为,解题策略的形成过程要以体验为主线、以有序为核心、以应用为契机,在呈现方式上要体现出过程性,凸显活动的有效性,在不同的学习阶段,从不同的角度,不断对它们进行反思,在活动中促进其目标达成。
1. 以体验为主线
策略意识的形成解决了学生选择合适方法的问题,但是各式各样的策略不能只由教师讲解、学生记忆的方式灌输给学生,学生还要经历体验的过程。
经历了,不一定会获得丰富的经验,但并不意味着没有一点收获,这样的现实说明,活动未必产生经验。同样的,数学活动未必会产生数学活动经验,要想在体验中积累活动经验,必须要引起思维的关注,并且思维关注要有相应的对象,经验有个性化的倾向,数学活动经验的提出关注的是教师引导的作用。
在策略获得的过程中,我们可以创设有数学研究目的的活动,让学生在反复的获取中强化经验,知晓策略形成的过程,经历对策略认知的过程,有目的地体验是获取策略的重要方式。
例如,教师可以设置这样的针对性体验活动让学生积累一定的经验:
(1)给出计算器,请学生拨珠表示12、10、16、20.
(2)说出拨珠表示12、10、16、20的理由。
(3)题组训练,给出已拨珠的计数器说出数字;给出数字在计数器上拨珠表示;有2颗珠子在计数器上可以表示出哪些数,并说说理由。
(4)错误反思:没有理解两位数的组成意义,没看清楚个位与十位。
学生在体验过程中明确了:十位上的珠子个数表示几个十,个位上珠子个数表示几个一。笔者以为,数学活动并非一定是动手操作,让学生经历犯错的过程和体验纠正错误的过程,引导学生去感悟自己错误的原因,形成防止再错的对策,对学生的策略形成有着积极的作用。
2. 以有序为核心
邵瑞珍教授认为:"解决问题的策略,通常指学习者选择、组合、改变或者操作背景命题(学生的认知结构中与当前问题解答有关的事实、概念与原理)的一系列规则,以便填补问题的固有空隙。""策略指出一连串步骤,从差距的一端向另一端移动,其方向或者是逆向,即从要求达到的终端开始,向后一步一步地倒退,酷似任务分析;或是顺向,即从已知条件开始前进,直到终点。"
例如,在"6、7的分与合"一课的练习教学中,设置了"梳理引入-解决问题-探索发现"的教学环节,为揭示数学规律"差不变,被减数越大,减数越大;被减数越小,减数越小。被减数不变,减数越大,差越小"提供了操作保障。
在梳理引入环节,教师设置活动:出示6-□=□,组织学生思考后讨论,交流,汇报。学生先是说出心中所想答案,通过学生互评,发现可以有序说出6-□=□,进而教师出示7-□=□,学生有序回答。
在解决问题环节,教师指导学生拿数字卡片做数学游戏。
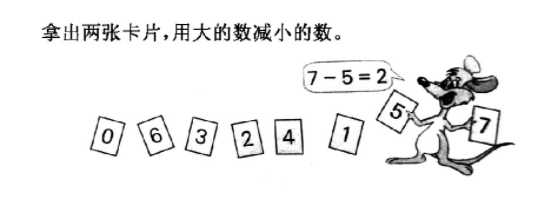
教师组织学生同桌之间进行练习,一个学生拿出两张卡片,另外一个学生用大的数减小的数说一道减法算式。
这个问题的解决需要学生构造数学模型,学生在解决问题时需要使用对应的策略---有序。教师要关注的是学生们思考本题的方式,以及思考的过程,可以采用如下的教学方式:
(1)学生先思考一分钟时间,能想多少就想多少。(2)学生两人小组讨论2~3分钟,并将想法与同伴交流。(3)全班汇报交流5~7分钟,根据总结列出表格的形式。在经历"个人思考-分组讨论-集体交流"之后,发现学生们对于有序、整理有了深层次理解。
建立数学模型:□-□=□。
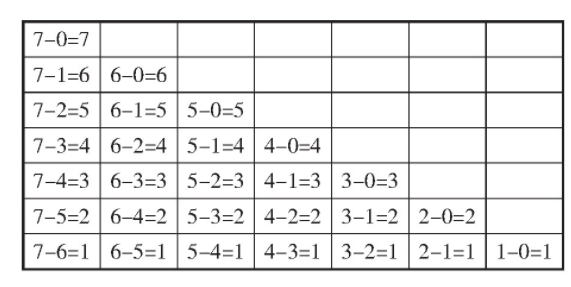
在此之后,引导学生在表格中找到□-□=2、□-4=□的算式。观察被减数与减数是如何变化的。
整个探究过程是有序的,既着眼于学生的知识经验,又关注了学生数学思维的推进,注重让学生在思考、交流的过程中获得丰富的学习体验。策略的功能就在于减少尝试与错误的任意性,节约解决问题所需要的时间,提高解答的效率。笔者以为策略讲究的是有序,要在纷乱复杂的问题中探寻解决这一类问题的方法,再以有序为核心,找寻策略形成的过程。
3. 以应用为契机
从意识到策略,最终目的都是应用。体会数学策略和生活的联系是很紧密的,学生在日常生活中会遇到很多客观存在的现象,要有一定的数学敏感性,要善于运用数学知识去解释这些现象,运用一定的策略,获得对现象本质的理解。如在教学一年级的解决实际问题时,我们常需要用到一定的策略。
(1)妈妈买了15个苹果,小明吃了一些,还剩10个,问小明一共吃了几个苹果?
(2)气球放飞了一半,还剩8个,原来有多少个?
(3)树上有18只鸟,第一次飞走了8只,第二次飞走的和第一次的同样多,两次一共飞走了多少只鸟?
学生们在读题后,分析题中所给的条件,选择相应的策略。如题(1)中,妈妈买的苹果-剩下的苹果=吃了的苹果;题(2)中,放飞的气球+剩下的气球=原来的气球,但学生们需根据题意,分析放飞的气球是多少;题(3)中,第一次飞走的+第二次飞走的=两次一共飞走的,需要学生们除了分析出第二次飞走的小鸟,还要排除18只鸟这个无效的条件。
简单的解题策略可以很快学会,但复杂的信息加工涉及许多策略,必须充分练习。因此,解题策略的教学一般不能立竿见影,必须坚持长期的、系统的教学训练方能取得满意的效果。
教师不能满足于把相关策略知识告诉学生,学生能说出相关内容就完成任务。重要的是教师要指导学生利用策略来指导自身完成相关练习,练习必须有连续性,没有连续性,学生将无所适从,其能力也不能形成。但在练习中必须有变化,如让学生与同伴一起通过变式练习运用解题策略,激发学生的数学思维,其知识才能深化,策略才能灵活应用。
参考文献
[1] 中华人民共和国教育部。义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]王光明,范文贵。新版课程标准解析与教学指导---小学数学[M].北京:北京师范大学出版社,2012.
[3] 邵瑞珍。教育心理学[M].上海:华东师范大学出版社,1996.





